The velocity of a wave is a fundamental property that describes how fast the wave propagates through a medium. Understanding the concept of wave velocity is crucial in various fields of physics, such as optics, acoustics, and electromagnetism. In this comprehensive guide, we will delve into the details of how to calculate the velocity of a wave using the formula v = fλ, where v is the velocity, f is the frequency, and λ is the wavelength.
The Wave Equation and Its Significance
The wave equation is a second-order partial differential equation that describes the propagation of waves through a medium. It relates the displacement of a wave to its spatial and temporal derivatives, and it is the foundation for understanding the behavior of waves. The wave equation can be written as:
∂²u/∂t² = c² ∇²u
where u is the displacement of the wave, t is time, and c is the wave velocity. The operator ∇² represents the Laplacian, which is a measure of the curvature of the wave function.
The wave equation is a fundamental equation in physics and is used to describe various types of waves, including electromagnetic waves, sound waves, and water waves. By solving the wave equation, we can derive the relationship between the wave velocity, frequency, and wavelength, which is the basis for the formula v = fλ.
The Formula for Wave Velocity: v = fλ
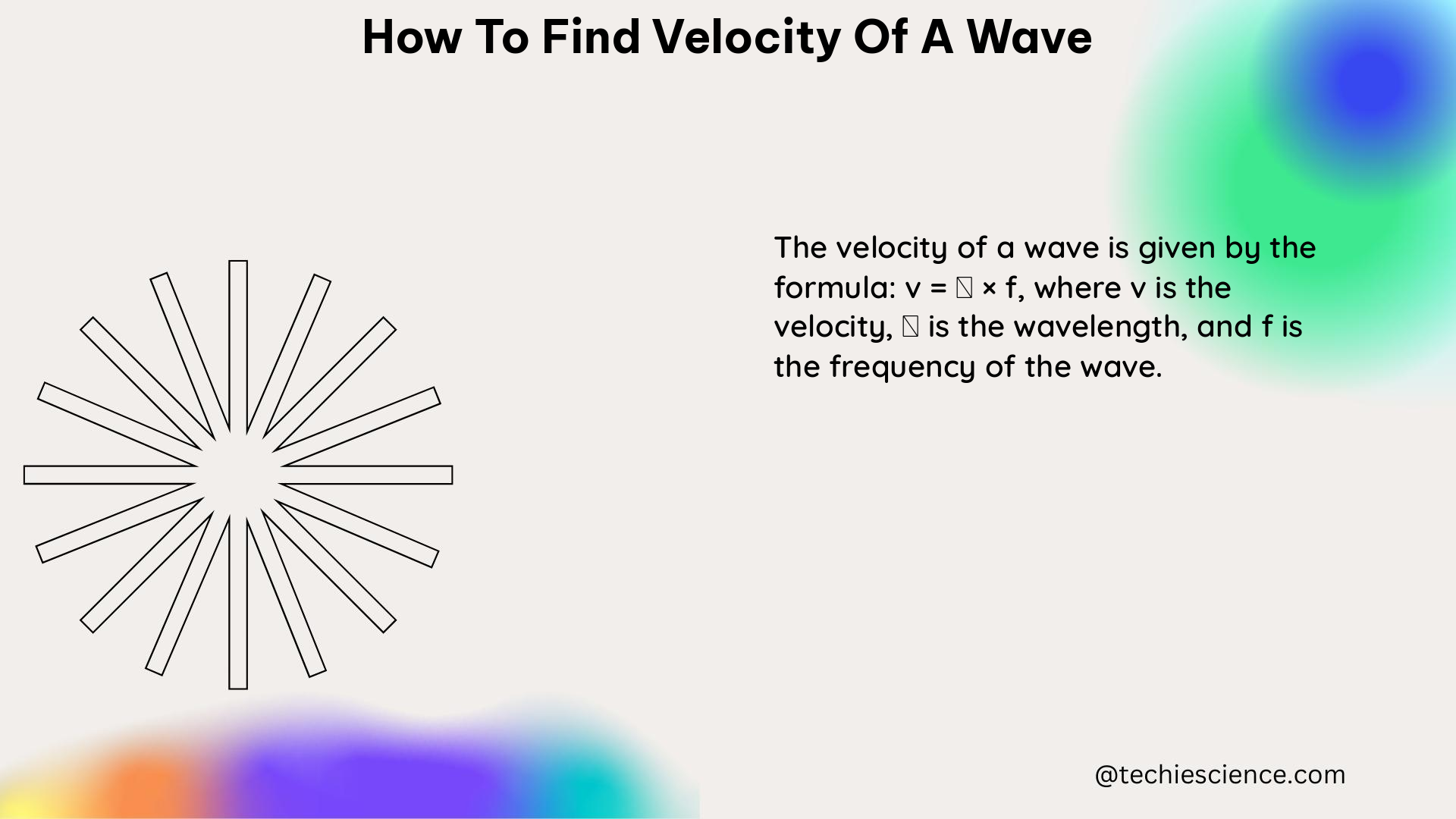
The formula for wave velocity, v = fλ, is a direct consequence of the wave equation. It states that the velocity of a wave is equal to the product of its frequency and wavelength. This relationship is valid for all types of waves, regardless of the medium through which they are propagating.
The frequency, f, is the number of wave cycles that pass a given point per unit of time, typically measured in Hertz (Hz). The wavelength, λ, is the distance between successive crests or troughs of the wave, typically measured in meters (m).
To calculate the wave velocity, we simply need to know the frequency and wavelength of the wave. For example, if we have a wave with a frequency of 100 Hz and a wavelength of 3 meters, we can calculate the velocity as follows:
v = fλ
v = (100 Hz)(3 m)
v = 300 m/s
Therefore, the velocity of the wave is 300 meters per second.
Factors Affecting Wave Velocity
The velocity of a wave is not only determined by the frequency and wavelength but also by the properties of the medium through which the wave is propagating. Some of the key factors that can affect the wave velocity include:
- Medium Properties:
- Density: The density of the medium can influence the wave velocity. For example, the speed of sound is higher in denser media, such as water, compared to less dense media, such as air.
-
Elasticity: The elasticity of the medium can also affect the wave velocity. Stiffer media, such as solids, generally have higher wave velocities compared to more flexible media, such as liquids and gases.
-
Temperature:
-
Temperature can have a significant impact on the wave velocity, particularly for sound waves. As the temperature of the medium increases, the speed of sound typically increases as well.
-
Pressure:
-
Pressure can also influence the wave velocity, especially for sound waves. Higher pressure generally leads to an increase in the speed of sound.
-
Frequency Dependence:
- In some cases, the wave velocity may depend on the frequency of the wave. This is known as dispersion, and it can occur in media with complex structures, such as optical fibers or certain types of materials.
Understanding these factors is crucial when working with waves in various applications, such as in the design of communication systems, the analysis of seismic data, or the study of wave propagation in biological tissues.
Examples and Numerical Problems
To further illustrate the concept of wave velocity, let’s consider some examples and numerical problems.
Example 1: Sound Waves in Air
– Frequency: 1000 Hz
– Wavelength: 0.34 m
– Calculate the velocity of the sound wave.
– v = fλ
– v = (1000 Hz)(0.34 m)
– v = 340 m/s
Example 2: Electromagnetic Waves in a Vacuum
– Frequency: 3 × 10^8 Hz (corresponding to visible light)
– Wavelength: 1 × 10^-6 m
– Calculate the velocity of the electromagnetic wave.
– v = fλ
– v = (3 × 10^8 Hz)(1 × 10^-6 m)
– v = 3 × 10^8 m/s (the speed of light in a vacuum)
Example 3: Water Waves in a Lake
– Frequency: 0.5 Hz
– Wavelength: 4 m
– Calculate the velocity of the water wave.
– v = fλ
– v = (0.5 Hz)(4 m)
– v = 2 m/s
These examples demonstrate the versatility of the formula v = fλ in calculating the velocity of different types of waves, including sound waves, electromagnetic waves, and water waves.
Practical Applications and Implications
The concept of wave velocity has numerous practical applications and implications in various fields of science and technology. Here are a few examples:
- Telecommunications:
-
In communication systems, the velocity of electromagnetic waves, such as radio waves and microwaves, is crucial for the design and optimization of transmitters, receivers, and signal propagation.
-
Seismology:
-
In the study of earthquakes and the Earth’s interior, the velocity of seismic waves is used to infer the structure and composition of the Earth’s layers.
-
Medical Imaging:
-
In medical imaging techniques, such as ultrasound and magnetic resonance imaging (MRI), the velocity of sound waves or electromagnetic waves is used to generate images of the human body.
-
Oceanography:
-
The velocity of water waves is important in the study of ocean currents, tides, and the propagation of tsunamis.
-
Acoustics:
- The velocity of sound waves is crucial in the design of musical instruments, room acoustics, and noise control applications.
Understanding the concept of wave velocity and its underlying principles is essential for many scientific and technological advancements. By mastering the formula v = fλ and the factors that influence wave velocity, you can gain a deeper understanding of the behavior of waves and their applications in various fields.
Conclusion
In this comprehensive guide, we have explored the fundamental concept of wave velocity and how to calculate it using the formula v = fλ. We have discussed the wave equation, the significance of the formula, and the factors that can affect the wave velocity. Additionally, we have provided examples and numerical problems to reinforce the understanding of this important concept.
By mastering the techniques and principles presented in this guide, you will be well-equipped to tackle a wide range of problems and applications involving wave propagation in various fields of physics and engineering.
References:
- Serway, R. A., & Jewett, J. W. (2018). Physics for Scientists and Engineers with Modern Physics (10th ed.). Cengage Learning.
- Tipler, P. A., & Mosca, G. (2008). Physics for Scientists and Engineers (6th ed.). W. H. Freeman.
- Hecht, E. (2016). Optics (5th ed.). Pearson.
- Kinsler, L. E., Frey, A. R., Coppens, A. B., & Sanders, J. V. (1999). Fundamentals of Acoustics (4th ed.). Wiley.

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.