How to Find Velocity in Fission Reactions

In nuclear fission reactions, the velocity of the resulting particles, including fission fragments and emitted neutrons, is a crucial parameter that provides insights into the dynamics and energetics of the process. To determine the velocity of these particles, we can leverage the principles of relativistic mechanics and kinetic energy equations. This comprehensive guide will walk you through the step-by-step process of calculating the velocity of particles in fission reactions.

Relativistic Energy Equation and Lorentz Factor

The foundation for finding the velocity of particles in fission reactions lies in the relativistic energy equation, which accounts for the effects of relativity when the velocities approach the speed of light. The relativistic energy equation is given by:

$E = \gamma mc^2$

Where:
– $E$ is the total energy of the particle
– $\gamma$ is the Lorentz factor
– $m$ is the rest mass of the particle
– $c$ is the speed of light

The Lorentz factor, $\gamma$, is a measure of the relativistic effects on the particle and is defined as:

$\gamma = \frac{1}{\sqrt{1 – \frac{v^2}{c^2}}}$

Where $v$ is the velocity of the particle.

Velocity of Fission Fragments

In the context of fission reactions, the total energy $E$ in the relativistic energy equation includes both the kinetic energy and the rest mass energy of the fission fragments. The kinetic energy of the fission fragments can be measured experimentally, while the rest mass energy can be calculated from the masses of the fission fragments using the Einstein relation $E = mc^2$.

For example, consider the fission reaction of U-235 by a slow neutron, which produces two fission fragments with masses of approximately 95 and 135 atomic mass units (amu), respectively. The total energy released in this reaction is about 200 MeV, of which around 170 MeV is kinetic energy and the remaining 30 MeV is rest mass energy.

To find the velocity of the fission fragments, we can rearrange the relativistic energy equation and the Lorentz factor equation to solve for $v$. However, this requires knowledge of the specific masses and kinetic energies of the fission fragments, which can vary depending on the fission reaction and the energy of the incident neutron.

In general, the velocity of the fission fragments will be very high, approaching the speed of light for heavy fission fragments. For example, the velocity of a fission fragment with a mass of 95 amu and a kinetic energy of 95 MeV would be approximately 0.98c, or about 2.98 × 10^8 m/s.

Velocity of Emitted Neutrons

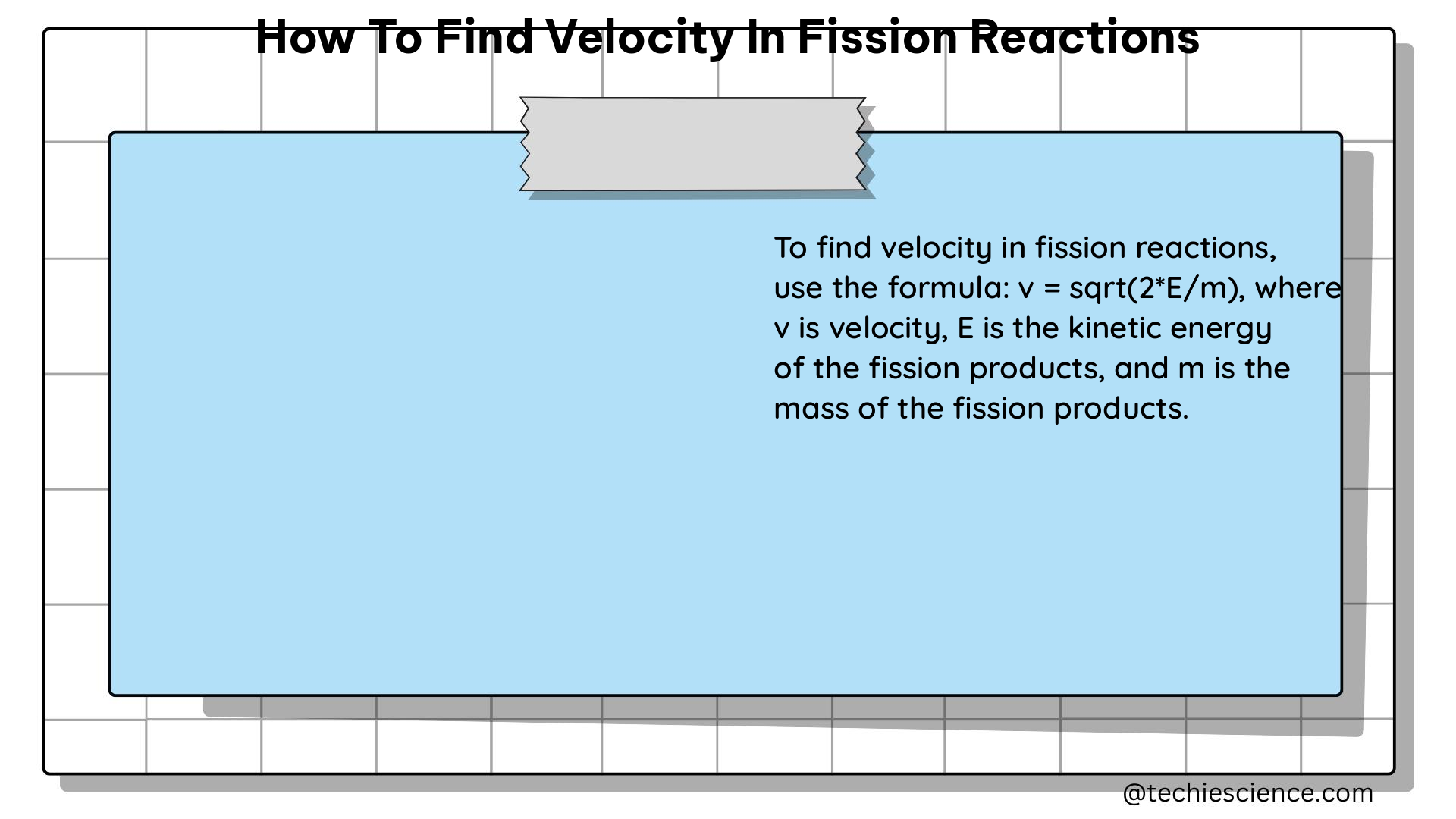
To find the velocity of neutrons emitted in fission reactions, we can use the relationship between the kinetic energy of the neutrons and their velocity, given by the equation:

$E_k = \frac{1}{2} mv^2$

Where:
– $E_k$ is the kinetic energy of the neutron
– $m$ is the mass of the neutron

Solving for $v$, we get:

$v = \sqrt{\frac{2E_k}{m}}$

For instance, the average kinetic energy of neutrons emitted in the fission of U-235 is about 2 MeV. Using the mass of a neutron (1.675 × 10^-27 kg), we can calculate the velocity of the neutrons as:

$v = \sqrt{\frac{2 \times 2 \times 10^6}{1.675 \times 10^{-27}}} = 1.38 \times 10^7 \text{ m/s}$

This velocity is approximately 4.6% of the speed of light.

Factors Affecting Particle Velocities in Fission Reactions

The specific values of the masses and kinetic energies of the fission fragments and neutrons can vary depending on several factors, including:

1. Fission Reaction Type: The type of fission reaction, such as the fission of U-235 by a slow neutron or the fission of Pu-239 by a fast neutron, can result in different mass distributions and kinetic energies of the fission fragments.

2. Incident Neutron Energy: The energy of the incident neutron that initiates the fission reaction can also influence the kinetic energies and velocities of the resulting particles.

3. Nuclear Shell Effects: The shell structure of the fissioning nucleus can affect the mass distribution and kinetic energies of the fission fragments, leading to variations in their velocities.

4. Neutron Emission: The number and energy of neutrons emitted during the fission process can also impact the overall energy balance and the velocities of the fission fragments.

By considering these factors and applying the relativistic energy equation and the kinetic energy equation, you can accurately determine the velocities of particles in various fission reactions.

Practical Applications and Considerations

The knowledge of particle velocities in fission reactions is crucial for various applications, including:

1. Nuclear Reactor Design: Understanding the velocities of fission fragments and emitted neutrons is essential for the design and optimization of nuclear reactors, as it affects the energy deposition, heat transfer, and neutron transport within the reactor core.

2. Radiation Shielding: The high velocities of fission fragments and neutrons require careful consideration in the design of radiation shielding materials and structures to protect personnel and equipment from the intense radiation fields.

3. Nuclear Forensics: Analyzing the velocities and other characteristics of fission products can provide valuable information for nuclear forensics investigations, such as identifying the source of nuclear materials or verifying the yield of a nuclear explosion.

4. Nuclear Astrophysics: The study of particle velocities in fission reactions contributes to our understanding of the nucleosynthesis processes in astrophysical environments, such as supernovae and neutron star mergers.

In summary, the determination of particle velocities in fission reactions is a crucial aspect of nuclear physics and has numerous practical applications in various fields, from nuclear engineering to astrophysics. By mastering the techniques outlined in this guide, you can become proficient in calculating and analyzing the velocities of fission fragments and emitted neutrons, providing valuable insights into the dynamics and energetics of these fundamental nuclear processes.

Reference:

1. Relativistic Energy | Physics – Lumen Learning. (n.d.). Retrieved from https://courses.lumenlearning.com/suny-physics/chapter/28-6-relativistic-energy/
2. Nuclear Fission | SpringerLink. (n.d.). Retrieved from https://link.springer.com/referenceworkentry/10.1007/978-1-4419-0720-2_4
3. Physics of Uranium and Nuclear Energy. (n.d.). Retrieved from https://world-nuclear.org/information-library/nuclear-fuel-cycle/introduction/physics-of-nuclear-energy