Summary
Finding the total acceleration of an object is a fundamental concept in physics, as it allows us to understand the motion and dynamics of various systems. The formula to calculate the total acceleration is atotal=√a2tan+a2n, where atotal is the total acceleration, atan is the tangential acceleration, and an is the normal acceleration. This formula is derived from the Pythagorean theorem, as tangential and normal acceleration are perpendicular to each other. In this comprehensive guide, we will delve into the details of how to find total acceleration, including the underlying physics principles, practical applications, and step-by-step examples.
Understanding Tangential and Normal Acceleration
Tangential acceleration, atan, is responsible for changes in the speed of an object, while normal acceleration, an, is responsible for changes in the direction of an object. For a car, the force causing this acceleration is the friction between the car and the pavement. If the turn is banked, the force is at least partially due to a component of the weight.
To better understand the relationship between tangential and normal acceleration, let’s consider a simple example of a car moving in a circular path. The car’s velocity can be broken down into two components: the tangential velocity, which is the speed of the car, and the normal velocity, which is the change in the direction of the car’s motion. Similarly, the car’s acceleration can be broken down into tangential acceleration, which is the change in the car’s speed, and normal acceleration, which is the change in the direction of the car’s motion.
Calculating Total Acceleration
The formula to calculate the total acceleration is:
atotal=√a2tan+a2n
Where:
– atotal is the total acceleration
– atan is the tangential acceleration
– an is the normal acceleration
This formula is derived from the Pythagorean theorem, as tangential and normal acceleration are perpendicular to each other.
To find the total acceleration, you need to first calculate the tangential and normal acceleration components. The tangential acceleration can be found using the formula:
atan = dv/dt
Where:
– atan is the tangential acceleration
– dv is the change in velocity
– dt is the change in time
The normal acceleration can be found using the formula:
an = v^2/r
Where:
– an is the normal acceleration
– v is the velocity of the object
– r is the radius of the circular path
Once you have the values for atan and an, you can plug them into the total acceleration formula to find the total acceleration.
Units and Coordinate Systems
When measuring acceleration, it’s important to consider the units being used. In physics, acceleration is often measured in meters per second squared (m/s^2). However, other units, such as feet per second squared (ft/s^2) or even standard gravity (g), may also be used.
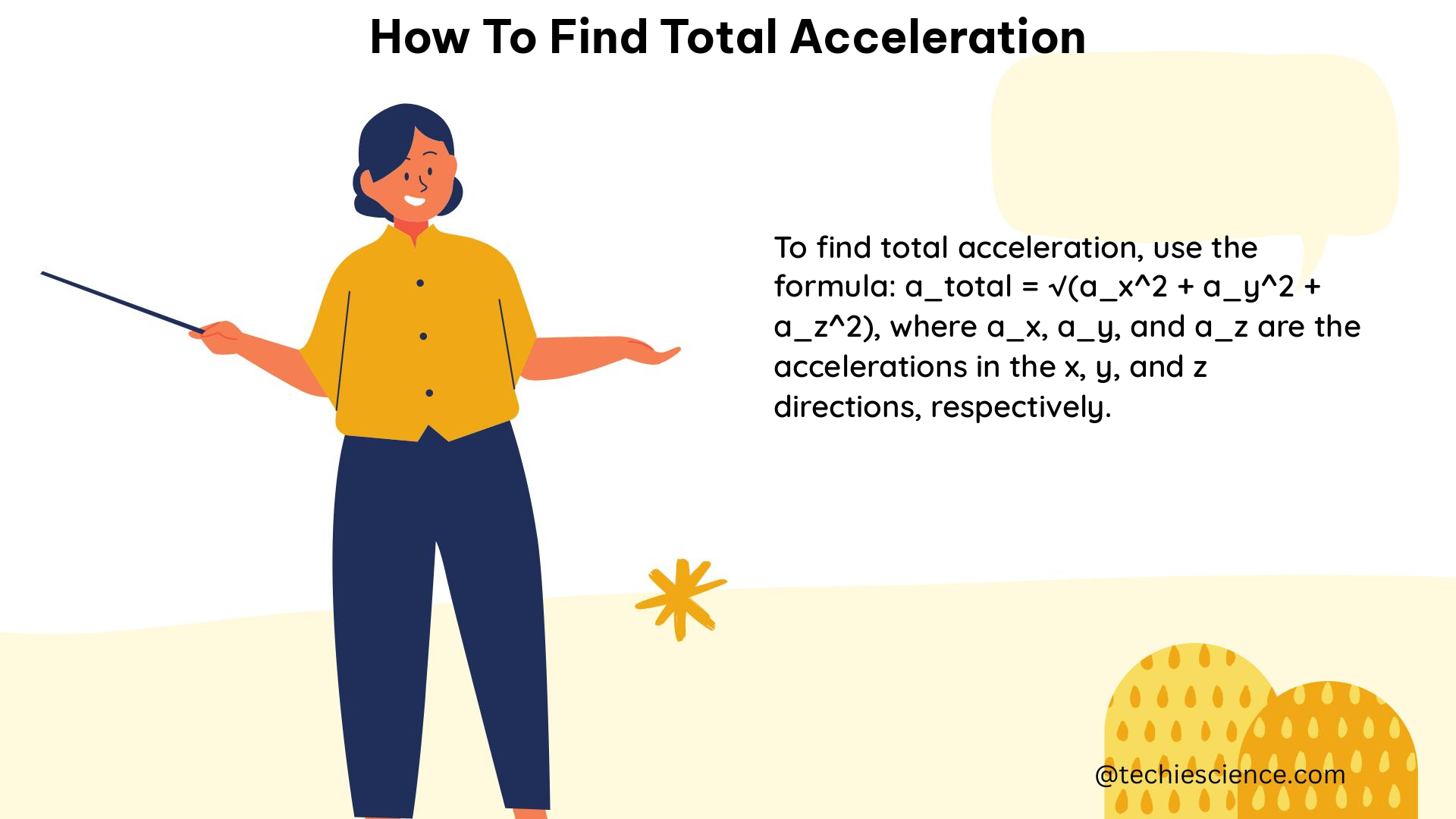
In practice, finding total acceleration often involves breaking down a problem into its component parts. For example, if you’re dealing with an object moving in three dimensions, you might need to find the acceleration in each of the x, y, and z directions, and then use the Pythagorean theorem to combine these into a total acceleration vector.
Positive and Negative Acceleration
It’s also important to note that acceleration can be positive or negative, depending on the direction of the acceleration. A negative acceleration simply means that the object is slowing down, while a positive acceleration means that the object is speeding up.
For example, if a car is slowing down, the tangential acceleration would be negative, as the car’s speed is decreasing. However, the normal acceleration would still be positive, as the car is still changing direction.
Using Free Body Diagrams
When working with acceleration, it’s often helpful to use free body diagrams to visualize the forces acting on an object. These diagrams can help you identify the various components of acceleration and how they relate to each other.
For instance, in the case of a car moving in a circular path, a free body diagram would show the forces acting on the car, such as the normal force, the weight of the car, and the frictional force. By analyzing these forces, you can determine the tangential and normal acceleration components and use them to calculate the total acceleration.
Examples and Numerical Problems
To further illustrate the concepts of finding total acceleration, let’s consider a few examples and numerical problems.
Example 1: A car moving in a circular path
A car is moving in a circular path with a radius of 50 meters. The car’s speed is 20 m/s. Calculate the total acceleration of the car.
Given:
– Radius of the circular path, r = 50 m
– Velocity of the car, v = 20 m/s
Step 1: Calculate the normal acceleration
an = v^2/r = (20 m/s)^2 / 50 m = 8 m/s^2
Step 2: Assume the tangential acceleration is zero (the car is moving at a constant speed)
atan = 0 m/s^2
Step 3: Calculate the total acceleration
atotal = √(atan^2 + an^2) = √(0^2 + 8^2) = 8 m/s^2
Therefore, the total acceleration of the car is 8 m/s^2.
Example 2: A ball thrown in the air
A ball is thrown upward with an initial velocity of 20 m/s. Assume the acceleration due to gravity is -9.8 m/s^2. Calculate the total acceleration of the ball at the highest point of its trajectory.
Given:
– Initial velocity, v0 = 20 m/s
– Acceleration due to gravity, g = -9.8 m/s^2
Step 1: At the highest point, the velocity of the ball is zero, so the tangential acceleration is zero.
atan = 0 m/s^2
Step 2: The normal acceleration is the acceleration due to gravity.
an = g = -9.8 m/s^2
Step 3: Calculate the total acceleration
atotal = √(atan^2 + an^2) = √(0^2 + (-9.8)^2) = 9.8 m/s^2
Therefore, the total acceleration of the ball at the highest point of its trajectory is 9.8 m/s^2 in the downward direction.
These examples demonstrate how to apply the formula for finding total acceleration and the importance of considering the tangential and normal acceleration components. By understanding these concepts, you can confidently solve a variety of problems involving the motion of objects in different scenarios.
Conclusion
Finding the total acceleration of an object is a fundamental skill in physics, as it allows us to understand the motion and dynamics of various systems. By using the formula atotal=√a2tan+a2n, and considering the tangential and normal acceleration components, as well as the units and coordinate systems involved, you can effectively calculate the total acceleration of an object.
Through the examples and numerical problems presented in this guide, you should now have a comprehensive understanding of how to find total acceleration. Remember to always break down the problem into its component parts, use free body diagrams to visualize the forces, and consider the direction of the acceleration. With practice, you’ll become proficient at solving a wide range of problems involving total acceleration.
References
- Is there only one way to solve for total acceleration?
- How do I get the total acceleration from 3 axes?
- Acceleration
- Calculating Total Acceleration

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.