As a mathematics student, understanding how to find the vertex of a parabola in factored form is a crucial skill. The vertex of a parabola is the point where the graph reaches its maximum or minimum value, and it plays a significant role in solving various problems. In this blog post, we will dive into the specific techniques and steps needed to accurately determine the vertex of a parabola in factored form.
What is the Factored Form of a Parabola?
The factored form of a quadratic equation is expressed as:
![]()
Where:
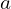 is the vertical stretch or compression factor
is the vertical stretch or compression factor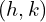 represents the vertex coordinates
represents the vertex coordinates
This form allows us to easily identify the vertex without the need for complex calculations.
How to Find the Vertex Coordinates?
To find the vertex coordinates ![]() from the factored form, follow these steps:
from the factored form, follow these steps:
- Identify the value of
 :
:
- Look at the expression inside the parentheses,
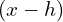
- The value of
 is the number being subtracted from
is the number being subtracted from 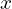
- For example, if the factored form is
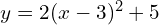 , then
, then 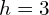
- Identify the value of
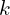 :
:
- The value of
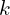 is the constant term added at the end of the equation
is the constant term added at the end of the equation - In the previous example,
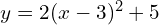 , we have
, we have 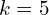
- Write the vertex coordinates:
- The vertex coordinates are
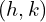
- In our example, the vertex coordinates would be
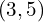
| Step | Explanation | Example |
|---|---|---|
| 1 | Identify the value of | |
| 2 | Identify the value of | |
| 3 | Write the vertex coordinates | Vertex coordinates: |
Advanced Techniques for Finding the Vertex
In some cases, the factored form may not be readily apparent. Here are a few advanced techniques to handle such situations:
Completing the Square
If the quadratic equation is in standard form, ![]() , you can use the completing the square method to convert it into factored form:
, you can use the completing the square method to convert it into factored form:
- Group the terms with
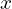 :
: 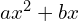
- Factor out the coefficient of
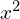 :
: 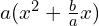
- Add and subtract the square of half the coefficient of
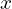 :
: 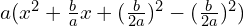
- Complete the square inside the parentheses:
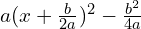
- Simplify and identify the vertex coordinates
Using the Quadratic Formula
Another advanced technique is to use the quadratic formula to find the roots of the equation and then calculate the midpoint between the roots:
- Given the quadratic equation
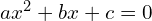 , use the quadratic formula:
, use the quadratic formula: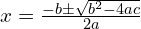
- Calculate the roots
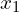 and
and 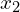
- Find the midpoint between the roots:
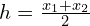
- Substitute
 into the original equation to find
into the original equation to find 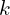
Troubleshooting and Pitfalls
- Make sure to correctly identify the values of
 and
and 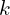 from the factored form
from the factored form - Be careful with signs when completing the square or using the quadratic formula
- Double-check your calculations to ensure accuracy
By understanding these specific techniques and advanced methods, you’ll be well-equipped to find the vertex of a parabola in factored form. Practice applying these concepts to various problems to reinforce your skills and deepen your understanding of this essential mathematical concept.

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.