Understanding how to find the slope of a graph is an essential skill in mathematics and physics. The slope of a graph represents the rate at which the dependent variable changes with respect to the independent variable. It tells us how steep or shallow a line or curve is. In this blog post, we will explore various methods to find the slope of a graph, including straight lines and curves. So let’s dive in!
How to Find the Slope of a Graph
Identifying the Rise and Run on a Graph
Before we can calculate the slope of a graph, we first need to understand the concepts of rise and run. Rise refers to the vertical change between two points on the graph, while run represents the horizontal change. The slope is then defined as the ratio of rise to run.
To identify the rise and run on a graph, choose two points on the line or curve. Let’s consider the following example:
Suppose we have a graph with two points, A(x₁, y₁) and B(x₂, y₂). The rise between these points is given by the difference in the y-coordinates: rise = y₂ – y₁. Similarly, the run is determined by the difference in the x-coordinates: run = x₂ – x₁.
Calculating the Slope of a Straight Line Graph
Calculating the slope of a straight line graph is relatively straightforward. We can use the formula:
![]()
Let’s work through an example to illustrate this:
Example: Find the slope of the line passing through the points (-2, 5) and (4, 9).
Solution: We can plug the values into the slope formula:
![]()
Therefore, the slope of the line is ![]() .
.
Worked Out Examples on Finding the Slope of a Straight Line Graph
Let’s practice finding the slope of a straight line graph with a few more examples:
Example 1: Find the slope of the line passing through the points (-3, 2) and (1, 8).
Solution: Using the slope formula, we have:
![]()
Therefore, the slope of the line is ![]() .
.
Example 2: Find the slope of the line passing through the points (2, 7) and (2, -3).
Solution: Here, we can observe that the x-coordinates of both points are the same. In such cases, the slope is undefined, as the run is zero. Therefore, the line is vertical, and its slope is undefined.
Finding the Slope of a Curve
Understanding the Concept of Slope for Curved Lines
Finding the slope of a curve requires a slightly different approach compared to straight lines. In the case of a curve, the slope at any point is given by the tangent line to the curve at that particular point. The tangent line represents the instantaneous rate of change at that point.
Techniques to Calculate the Slope of a Curve
To calculate the slope of a curve, we can use calculus and differentiate the equation of the curve with respect to the independent variable. The derivative, at any given point, represents the slope.
Let’s consider a simple example to illustrate this:
Example: Find the slope of the curve represented by the equation y = x² at the point (2, 4).
Solution: To find the slope at a point on a curve, we need to differentiate the equation with respect to x. In this case, differentiating y = x² gives us:
![]()
Substituting x = 2 into the derivative:

Therefore, the slope of the curve at the point (2, 4) is 4.
Worked Out Examples on Finding the Slope of a Curve
Let’s solve a couple more examples to solidify our understanding of finding the slope of a curve:
Example 1: Find the slope of the curve represented by the equation y = 3x³ + 2x² – 5x + 6 at the point (1, 6).
Solution: Differentiating the equation y = 3x³ + 2x² – 5x + 6 with respect to x, we get:
![]()
Substituting x = 1 into the derivative:
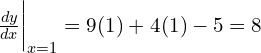
Therefore, the slope of the curve at the point (1, 6) is 8.
Example 2: Find the slope of the curve represented by the equation y = sin(x) at the point (π/2, 1).
Solution: Taking the derivative of y = sin(x) with respect to x, we have:
![]()
Substituting x = π/2 into the derivative:
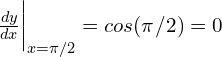
Hence, the slope of the curve at the point (π/2, 1) is 0.
Special Cases in Finding the Slope of a Graph

Determining the Slope of a Horizontal Line
A horizontal line has the same y-coordinate at every point, meaning there is no vertical change (rise). Therefore, the slope of a horizontal line is always 0.
Determining the Slope of a Vertical Line
A vertical line has the same x-coordinate at every point, resulting in no horizontal change (run). In this case, the slope is undefined.
How to Handle Undefined and Zero Slopes
When the slope is undefined, it means the curve or line is vertical. When the slope is zero, it indicates a horizontal line. These special cases are important to note when analyzing a graph.
How is finding the slope of a graph related to finding average velocity in physics?
When studying the concepts of calculus and motion in physics, both finding the slope of a graph and calculating average velocity play important roles. By determining the slope of a graph, we can understand the rate of change of a variable over a given interval. This concept is closely related to velocity, which represents the rate at which an object changes its position. In physics, average velocity is calculated by dividing the change in position by the time taken. By understanding how to find the slope of a graph, we can gain insights into finding average velocity in physics. To learn more about the calculation of average velocity, please refer to the article on Finding average velocity in physics.
Numerical Problems on how to find the slope of a graph
Problem 1
Find the slope of the line passing through the points (2, 4) and (5, 10).
Solution:
To find the slope of a line passing through two points, we can use the formula:
![]()
Given the points (2, 4) and (5, 10), we can calculate the change in y and change in x as follows:
![]()
![]()
Substituting these values into the slope formula:
![]()
Therefore, the slope of the line passing through the points (2, 4) and (5, 10) is 2.
Problem 2
Determine the slope of the line that passes through the points (3, -1) and (7, 5).
Solution:
Using the slope formula:
![]()
We can calculate the change in y and change in x:
![]()
![]()
Substituting these values into the slope formula:
![]()
Hence, the slope of the line passing through the points ![]() .
.
Problem 3
Find the slope of the line that passes through the points (-2, -3) and (4, 1).
Solution:
By using the slope formula:
![]()
We can calculate the change in y and change in x:
![]()
![]()
Substituting these values into the slope formula:
![]()
Therefore, the slope of the line passing through the points ![]() .
.
Also Read:
- How to find tangential acceleration
- How to find horizontal velocity without time
- How to find centripetal acceleration
- How to find velocity with acceleration and mass
- How to find constant acceleration with distance and time
- How to find distance in velocity time graph
- How to find acceleration with velocity and distance
- How to find velocity without time
- How to find mass without acceleration
- How to find acceleration with a constant velocity
Hi,
I am Rabiya Khalid, I have completed my masters in Mathematics. Article writing is my passion and I have been professionally writing for more than a year now. Being a science student, I have a knack for reading and writing about science and everything related to it.
In my free time, I let out my creative side on a canvas.