How to Find the Acceleration: A Comprehensive Guide for Physics Students

Summary

Acceleration is a fundamental concept in physics that describes the rate of change in an object’s velocity over time. To find the acceleration of an object, you can use the formula a = Δv / Δt, where a is the acceleration, Δv is the change in velocity, and Δt is the change in time. This guide will provide you with a detailed, step-by-step approach to understanding and calculating acceleration, including theoretical explanations, formulas, examples, and numerical problems to help you master this essential topic in physics.

Understanding Acceleration

Acceleration is a vector quantity, meaning it has both magnitude and direction. It represents the change in an object’s velocity over a given time interval. The formula for acceleration is:

a = Δv / Δt

Where:
– a is the acceleration (in meters per second squared, m/s²)
– Δv is the change in velocity (in meters per second, m/s)
– Δt is the change in time (in seconds, s)

Acceleration can be positive or negative, depending on the direction of the change in velocity. Positive acceleration indicates an increase in velocity, while negative acceleration (also known as deceleration) indicates a decrease in velocity.

Constant Acceleration

If the rate of change in velocity is constant, the acceleration is also constant. In this case, the formula for acceleration can be simplified to:

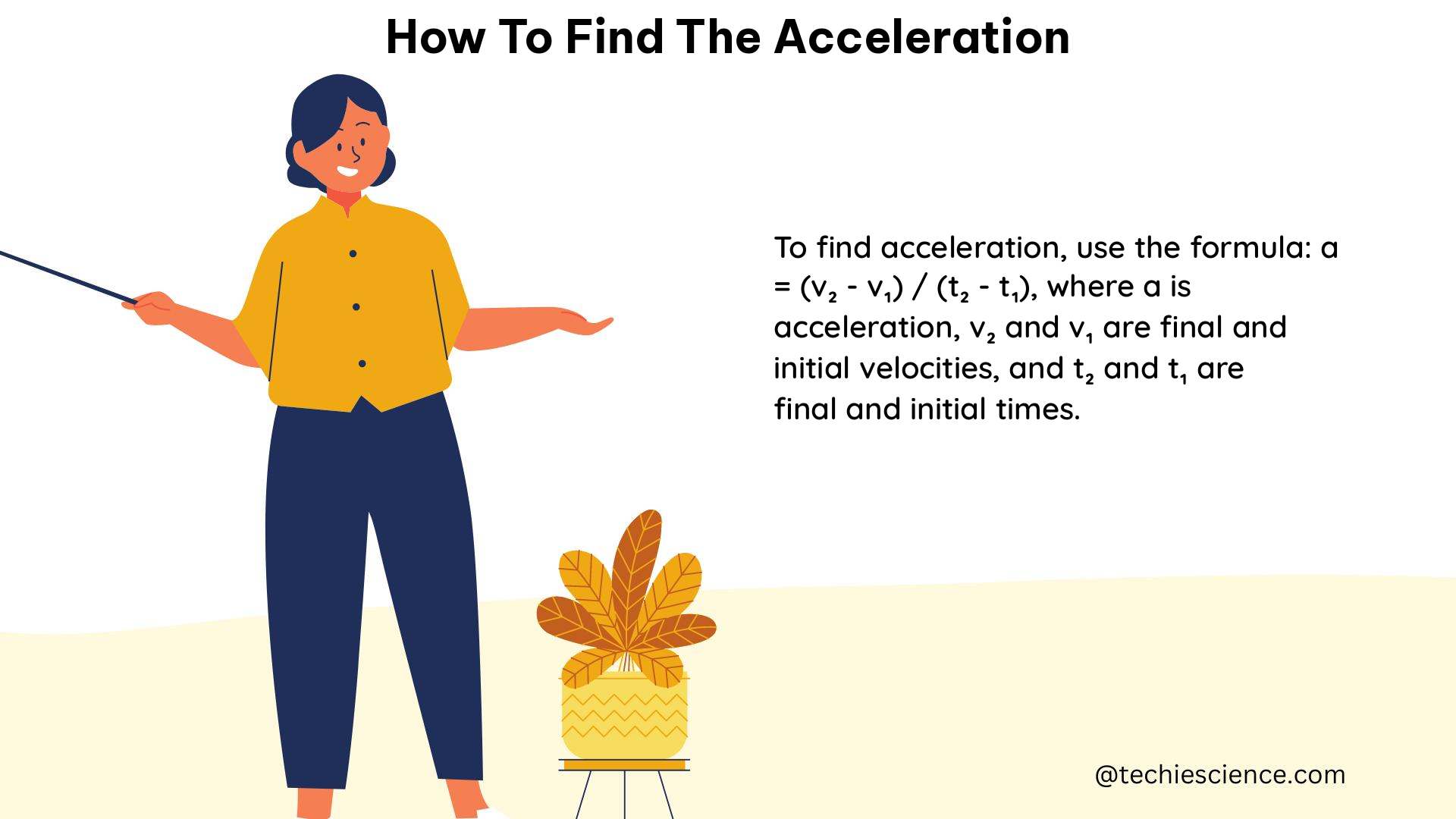
a = (v₂ - v₁) / (t₂ - t₁)

Where:
– v₁ is the initial velocity (in m/s)
– v₂ is the final velocity (in m/s)
– t₁ is the initial time (in s)
– t₂ is the final time (in s)

This formula allows you to calculate the acceleration of an object given its initial and final velocities, as well as the time interval.

Non-Constant Acceleration

If the rate of change in velocity is not constant, the acceleration will also not be constant. In this case, the acceleration must be calculated using the formula:

a = Δv / Δt

You will need to choose two specific points in time and calculate the change in velocity and the change in time between those points to determine the acceleration.

Measuring Acceleration

To measure the acceleration of an object, you can use various instruments, including:

1. Accelerometers: These devices measure the force of acceleration acting on an object and convert it into an electrical signal that can be measured and recorded.
2. Motion sensors: These sensors can track the position of an object over time and use the position data to calculate the velocity and acceleration.
3. Video analysis: By recording the motion of an object and analyzing the video frame by frame, you can calculate the changes in position, velocity, and acceleration.

When measuring acceleration, it is important to use accurate and precise instruments to ensure reliable results. Factors such as the sampling rate, resolution, and sensitivity of the measurement device can all affect the accuracy of the acceleration data.

Calculating Acceleration from a Data Table

To calculate the acceleration of an object from a data table, follow these steps:

1. Identify two points in the data table where you have the velocity and time values.
2. Calculate the change in velocity (Δv) between the two points.
3. Calculate the change in time (Δt) between the two points.
4. Divide the change in velocity by the change in time to find the acceleration:

a = Δv / Δt

For example, let’s say the data table shows the following information:

Time (s)	Velocity (m/s)
0	0
2	-10

To calculate the acceleration, we can use the formula:

a = Δv / Δt
a = (-10 m/s - 0 m/s) / (2 s - 0 s)
a = -5 m/s²

This means that the velocity of the object is decreasing by 5 meters per second every second, or the object is decelerating at a rate of 5 m/s².

Numerical Problems

1. An object has an initial velocity of 10 m/s and a final velocity of 30 m/s after 5 seconds. Calculate the acceleration of the object.

Given:
– Initial velocity (v₁) = 10 m/s
– Final velocity (v₂) = 30 m/s
– Time interval (Δt) = 5 s

Acceleration (a) = (v₂ – v₁) / Δt
a = (30 m/s – 10 m/s) / 5 s
a = 4 m/s²

1. A car accelerates from 0 m/s to 20 m/s in 4 seconds. Calculate the acceleration of the car.

Given:
– Initial velocity (v₁) = 0 m/s
– Final velocity (v₂) = 20 m/s
– Time interval (Δt) = 4 s

Acceleration (a) = (v₂ – v₁) / Δt
a = (20 m/s – 0 m/s) / 4 s
a = 5 m/s²

1. An object has a velocity of 15 m/s at time t = 0 s and a velocity of 5 m/s at time t = 3 s. Calculate the acceleration of the object.

Given:
– Initial velocity (v₁) = 15 m/s
– Final velocity (v₂) = 5 m/s
– Time interval (Δt) = 3 s

Acceleration (a) = (v₂ – v₁) / Δt
a = (5 m/s – 15 m/s) / 3 s
a = -3.33 m/s²

Graphical Representation of Acceleration

Acceleration can also be represented graphically using a velocity-time graph. The slope of the velocity-time graph represents the acceleration of the object. If the graph is a straight line, the acceleration is constant. If the graph is curved, the acceleration is not constant.

In the graph above, the slope of the line represents the constant acceleration of the object. The steeper the slope, the higher the acceleration.

Conclusion

Finding the acceleration of an object is a fundamental skill in physics. By understanding the formula a = Δv / Δt and applying it to data tables, numerical problems, and graphical representations, you can accurately calculate the acceleration of an object and gain a deeper understanding of its motion. Remember to use precise and accurate measurement instruments, and always consider the direction and constancy of the acceleration when analyzing your results.

References

• Calculating the Acceleration of an Object from a Data Table – YouTube
• Acceleration (video) – Khan Academy
• Physics archive > Unit 1Lesson 3: Acceleration – Khan Academy
• Measurable Quantity – an overview | ScienceDirect Topics
• Easy to perform quantitative experiments at home – Physics Forums
• Using accelerometer data to calculate distance – Physics Forums