How to Find Speed with Acceleration and Distance: A Comprehensive Guide

Finding speed with acceleration and distance is a fundamental concept in physics that is crucial for understanding and analyzing various types of motion. This comprehensive guide will provide you with a deep dive into the theoretical foundations, formulas, examples, and practical applications of this topic.

Understanding the Relationship between Speed, Acceleration, and Distance

The relationship between speed, acceleration, and distance can be expressed through the following equations:

1. Speed-Time Equation: v = u + at

2. Where v is the final speed, u is the initial speed, a is the acceleration, and t is the time.

3. Displacement-Time Equation: s = ut + (1/2)at^2

4. Where s is the displacement (distance), u is the initial speed, a is the acceleration, and t is the time.

5. Speed-Displacement Equation: v^2 = u^2 + 2as

6. Where v is the final speed, u is the initial speed, a is the acceleration, and s is the displacement (distance).

These equations form the foundation for understanding and solving problems related to finding speed with acceleration and distance.

Formulas for Finding Speed with Acceleration and Distance

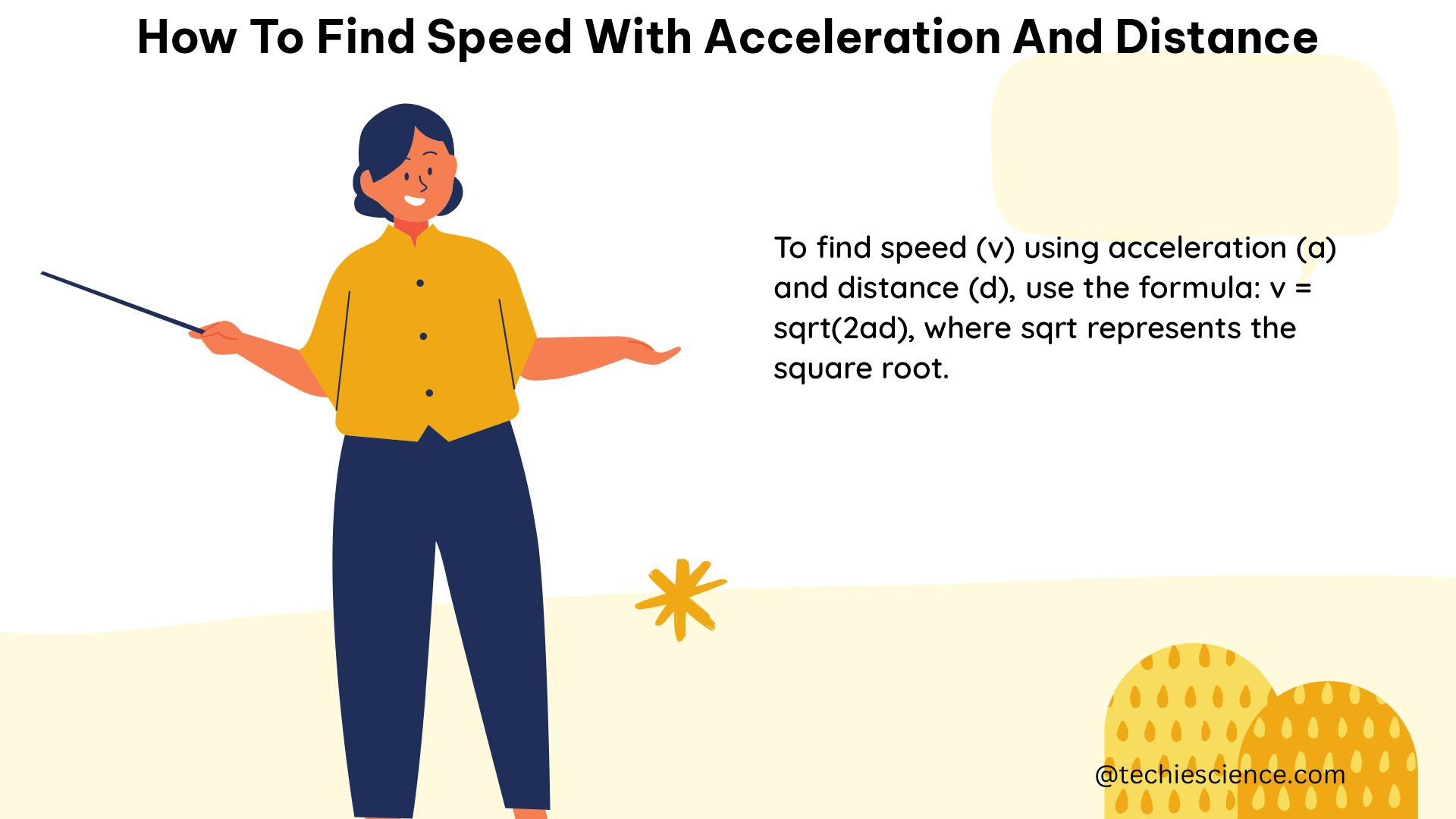
To find the speed with acceleration and distance, you can use the following formulas:

1. Speed-Time Formula: v = d/t

2. Where v is the speed, d is the distance, and t is the time.

3. Time-Acceleration-Distance Formula: t = √(2d/a)

4. Where t is the time, d is the distance, and a is the acceleration.

By combining these two formulas, you can find the speed as follows:

v = d/t = d/√(2d/a) = √(2ad)

This formula allows you to calculate the speed directly from the given acceleration and distance.

Examples and Numerical Problems

Let’s consider the following example:

A car accelerates from rest (initial speed = 0 m/s) to a final speed of 60 mph (26.82 m/s) over a distance of 1 mile (1609 m). Find the time taken and the final speed in m/s.

Given:
– Initial speed, u = 0 m/s
– Final speed, v = 26.82 m/s
– Distance, d = 1609 m

Step 1: Calculate the time taken using the Time-Acceleration-Distance Formula.
t = √(2d/a)

Since the car accelerates from rest, the initial speed u is 0 m/s. We can use the Speed-Displacement Equation to find the acceleration a:
v^2 = u^2 + 2ad
(26.82 m/s)^2 = (0 m/s)^2 + 2a(1609 m)
a = 0.5 m/s^2

Substituting the values, we get:
t = √(2 × 1609 m / 0.5 m/s^2)
t = 56.57 s

Step 2: Calculate the final speed in m/s.
v = d/t
v = 1609 m / 56.57 s
v = 28.44 m/s

Therefore, the car reaches a final speed of 28.44 m/s (or 107.28 km/h) over a distance of 1 mile (1609 m) with an acceleration of 0.5 m/s^2.

Here’s another example:

A ball is thrown upward with an initial velocity of 20 m/s. Assuming the acceleration due to gravity is -9.8 m/s^2, find the maximum height reached by the ball.

Given:
– Initial velocity, u = 20 m/s
– Acceleration, a = -9.8 m/s^2

We can use the Displacement-Time Equation to find the maximum height:
s = ut + (1/2)at^2

At the maximum height, the velocity is zero, so we can set v = 0:
0 = 20t - (1/2)(9.8)t^2
(1/2)(9.8)t^2 - 20t = 0
t = 0 s or t = 4.08 s

Substituting the time of 4.08 s into the Displacement-Time Equation, we get:
s = 20 × 4.08 - (1/2)(9.8)(4.08)^2
s = 81.6 m

Therefore, the maximum height reached by the ball is 81.6 m.

Practical Applications and Real-World Scenarios

The ability to find speed with acceleration and distance has numerous practical applications in various fields, including:

1. Transportation: Calculating the speed and acceleration of vehicles, such as cars, trains, and airplanes, is crucial for designing efficient transportation systems, ensuring safety, and optimizing fuel consumption.

2. Sports and Athletics: Analyzing the speed and acceleration of athletes during various sports activities, such as sprinting, jumping, and throwing, can help coaches and trainers optimize training programs and improve performance.

3. Engineering and Robotics: Designing and controlling the motion of robots, drones, and other mechanical systems often require the accurate calculation of speed, acceleration, and distance.

4. Physics Experiments: In physics laboratories, experiments involving the measurement of speed, acceleration, and distance are commonly used to verify and apply the principles of classical mechanics.

5. Ballistics and Projectile Motion: Understanding the relationship between speed, acceleration, and distance is essential for analyzing the trajectories of projectiles, such as bullets, missiles, and artillery shells.

By mastering the concepts and techniques presented in this guide, you will be well-equipped to tackle a wide range of problems and scenarios involving the determination of speed with acceleration and distance.

Conclusion

In this comprehensive guide, we have explored the fundamental principles, formulas, and practical applications of finding speed with acceleration and distance. By understanding the underlying relationships between these key variables, you can confidently solve a variety of problems in physics and engineering, and apply these concepts to real-world situations.

Remember, the ability to accurately calculate speed, acceleration, and distance is not only a valuable skill in the academic realm but also has far-reaching implications in various industries and fields of study. Mastering this topic will not only deepen your understanding of classical mechanics but also equip you with the tools to tackle complex problems and contribute to advancements in science and technology.

References

1. Velocity in Math: Definition, Equation & Problems – Lesson – Study.com
2. Find speed using distance and acceleration? – Physics Forums
3. Quantitative Motion Analysis – Body Physics: Motion to Metabolism
4. Velocity – Definition, Units, Formula, Examples, Equations, Video …
5. How to Calculate Time and Distance from Acceleration and Velocity