In the realm of physics, understanding the concept of resultant acceleration is crucial for analyzing the motion of objects and solving complex problems. Resultant acceleration is the vector sum of all the accelerations acting on an object, and it represents the net acceleration experienced by the object. This comprehensive guide will walk you through the step-by-step process of finding the resultant acceleration, equipping you with the necessary knowledge and tools to tackle a wide range of physics problems.
Identifying the Components of Acceleration
The first step in finding the resultant acceleration is to identify the x and y components of the acceleration vector. This involves breaking down the acceleration into its horizontal (x) and vertical (y) components. By doing so, you can effectively analyze the motion of the object in both dimensions.
To illustrate this concept, let’s consider an example. Suppose an object is experiencing an acceleration of 3 m/s^2 in the x-direction and 4 m/s^2 in the y-direction. In this case, the x-component of the acceleration is 3 m/s^2, and the y-component is 4 m/s^2.
Ensuring Consistent Units
Before proceeding with the calculations, it is crucial to ensure that the units of the acceleration components are consistent. In the field of physics, the standard unit for acceleration is meters per second squared (m/s^2). Ensuring that all the acceleration values are expressed in this unit will simplify the subsequent calculations and ensure accurate results.
Calculating the Magnitude of Resultant Acceleration
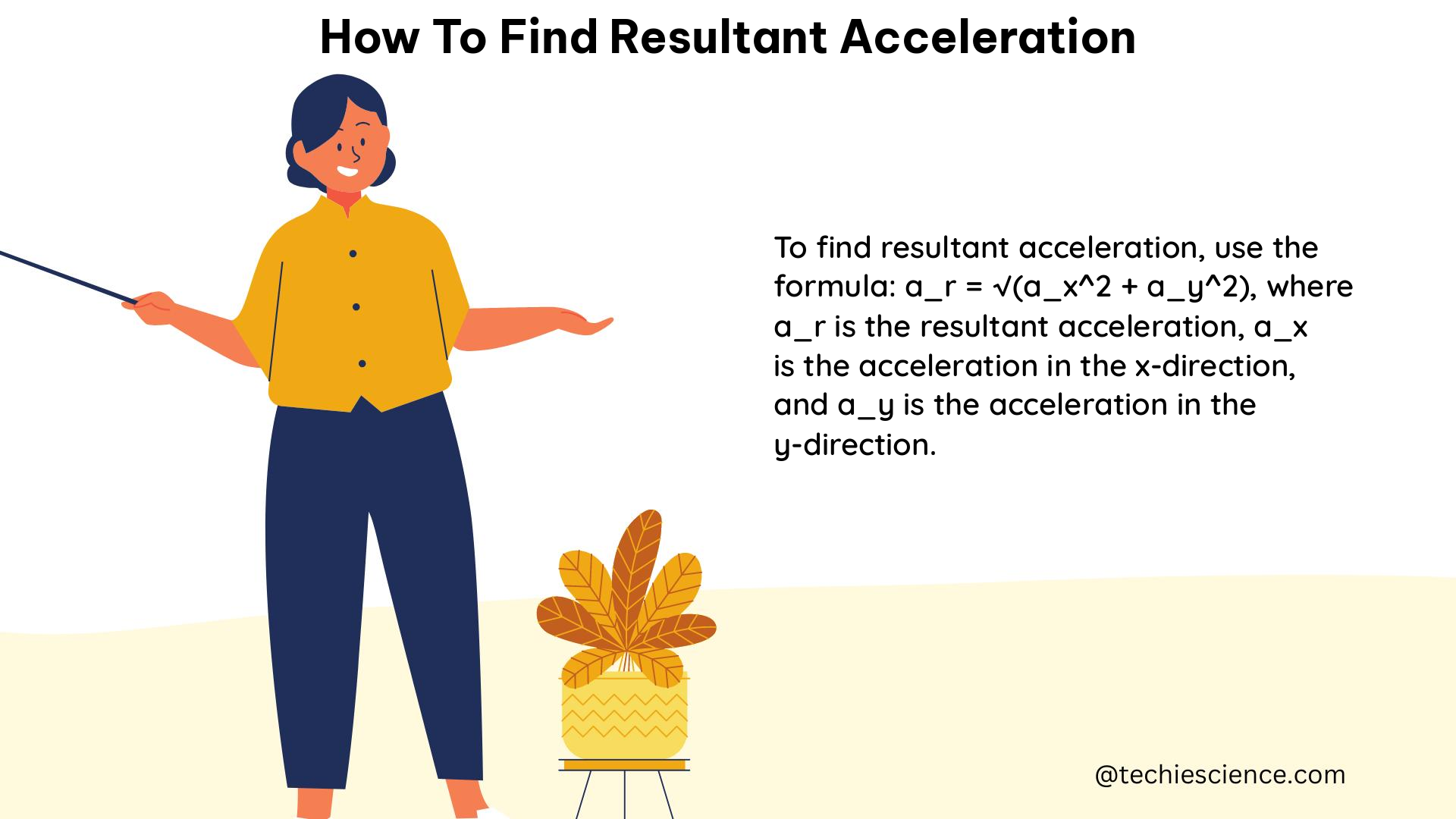
To find the magnitude of the resultant acceleration, we can use the Pythagorean theorem. The formula for the magnitude of the resultant acceleration (a_resultant) is:
a_resultant = √(a_x^2 + a_y^2)
where a_x is the x-component of the acceleration, and a_y is the y-component of the acceleration.
Continuing with the previous example, we can calculate the magnitude of the resultant acceleration as follows:
a_resultant = √(3^2 + 4^2)
a_resultant = √(9 + 16)
a_resultant = √25
a_resultant = 5 m/s^2
Therefore, the magnitude of the resultant acceleration is 5 m/s^2.
Determining the Direction of Resultant Acceleration
To determine the direction of the resultant acceleration, we can use trigonometry. The angle (θ) between the resultant acceleration vector and the x-axis can be calculated using the following formula:
θ = arctan(a_y / a_x)
In the example we’ve been using, the angle would be:
θ = arctan(4 / 3)
θ = 53.13 degrees
This means that the resultant acceleration is directed at an angle of 53.13 degrees north of east.
Visualizing the Resultant Acceleration
To better understand the concept of resultant acceleration, it can be helpful to visualize the acceleration vector and its components. You can create a diagram or sketch that shows the x and y components of the acceleration, as well as the resultant acceleration vector and its direction.

In the diagram, the x-component of the acceleration is represented by the horizontal arrow, the y-component is represented by the vertical arrow, and the resultant acceleration vector is shown as the diagonal arrow.
Applying the Concept to Physics Problems
Now that you have a solid understanding of the steps involved in finding the resultant acceleration, let’s explore some practical applications and examples.
Example 1: Projectile Motion
Suppose an object is launched with an initial velocity of 20 m/s at an angle of 30 degrees above the horizontal. Assuming no air resistance, find the resultant acceleration of the object at the highest point of its trajectory.
Given:
– Initial velocity (v_0) = 20 m/s
– Angle of launch (θ) = 30 degrees
Step 1: Identify the x and y components of the acceleration.
In projectile motion, the acceleration due to gravity (g) is the only force acting on the object, and it is directed downward (in the negative y-direction).
a_x = 0 m/s^2 (no acceleration in the x-direction)
a_y = -9.8 m/s^2 (acceleration due to gravity)
Step 2: Calculate the magnitude of the resultant acceleration.
a_resultant = √(a_x^2 + a_y^2)
a_resultant = √(0^2 + (-9.8)^2)
a_resultant = 9.8 m/s^2
Step 3: Determine the direction of the resultant acceleration.
θ = arctan(a_y / a_x)
θ = arctan(-9.8 / 0)
θ = -90 degrees (straight down)
Therefore, the resultant acceleration of the object at the highest point of its trajectory is 9.8 m/s^2 directed straight down.
Example 2: Inclined Plane
An object is placed on an inclined plane with an angle of 45 degrees. The coefficient of friction between the object and the plane is 0.2. Find the resultant acceleration of the object.
Given:
– Angle of the inclined plane (θ) = 45 degrees
– Coefficient of friction (μ) = 0.2
Step 1: Identify the x and y components of the acceleration.
The acceleration due to gravity (g) is the only force acting on the object, and it can be resolved into components parallel and perpendicular to the inclined plane.
a_x = g * sin(θ) – μ * g * cos(θ)
a_y = g * cos(θ)
Substituting the values:
a_x = 9.8 * sin(45°) – 0.2 * 9.8 * cos(45°)
a_x = 6.93 – 6.93 = 0 m/s^2
a_y = 9.8 * cos(45°) = 6.93 m/s^2
Step 2: Calculate the magnitude of the resultant acceleration.
a_resultant = √(a_x^2 + a_y^2)
a_resultant = √(0^2 + 6.93^2)
a_resultant = 6.93 m/s^2
Step 3: Determine the direction of the resultant acceleration.
θ = arctan(a_y / a_x)
θ = arctan(6.93 / 0)
θ = 90 degrees (straight up the inclined plane)
Therefore, the resultant acceleration of the object on the inclined plane is 6.93 m/s^2 directed straight up the inclined plane.
These examples demonstrate the application of the concepts and formulas discussed earlier to solve real-world physics problems involving resultant acceleration. By following the step-by-step approach, you can confidently tackle a wide range of problems and deepen your understanding of this fundamental topic in physics.
Conclusion
Mastering the art of finding resultant acceleration is a crucial skill for any physics student or enthusiast. By understanding the components of acceleration, ensuring consistent units, and applying the Pythagorean theorem and trigonometry, you can accurately determine the magnitude and direction of the resultant acceleration. The examples provided in this guide illustrate the practical application of these concepts, empowering you to tackle a variety of physics problems with confidence.
Remember, the key to success in physics is not just memorizing formulas, but rather developing a deep understanding of the underlying principles and their applications. By following the steps outlined in this comprehensive guide, you will be well on your way to becoming a proficient problem-solver in the realm of resultant acceleration.
References:
- AP Physics 1 Investigation 2: Newton’s Second Law
- How to Calculate an Object’s Resultant Acceleration from its Components
- Solving for Resultant Acceleration (Part 1) – YouTube
- Magnitude of the resultant acceleration – Physics Forums
- Resultant Vector Definition, Formula & Examples – Lesson – Study.com

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.