How to Find Radial Velocity of Stars: A Comprehensive Guide

The radial velocity of a star is a crucial parameter in observational astronomy, as it provides valuable information about the star’s motion along the line of sight. Determining the radial velocity of stars is essential for studying the dynamics of stellar systems, detecting exoplanets, and understanding the overall structure and evolution of the universe. In this comprehensive guide, we will delve into the technical details and step-by-step process of finding the radial velocity of stars.

Understanding the Doppler Shift

The foundation of measuring the radial velocity of stars lies in the Doppler shift, a phenomenon that describes the change in the observed wavelength of a light source due to its relative motion. When a star is moving towards or away from the observer, the wavelength of the light emitted by the star is shifted, either towards shorter (blue) or longer (red) wavelengths, respectively.

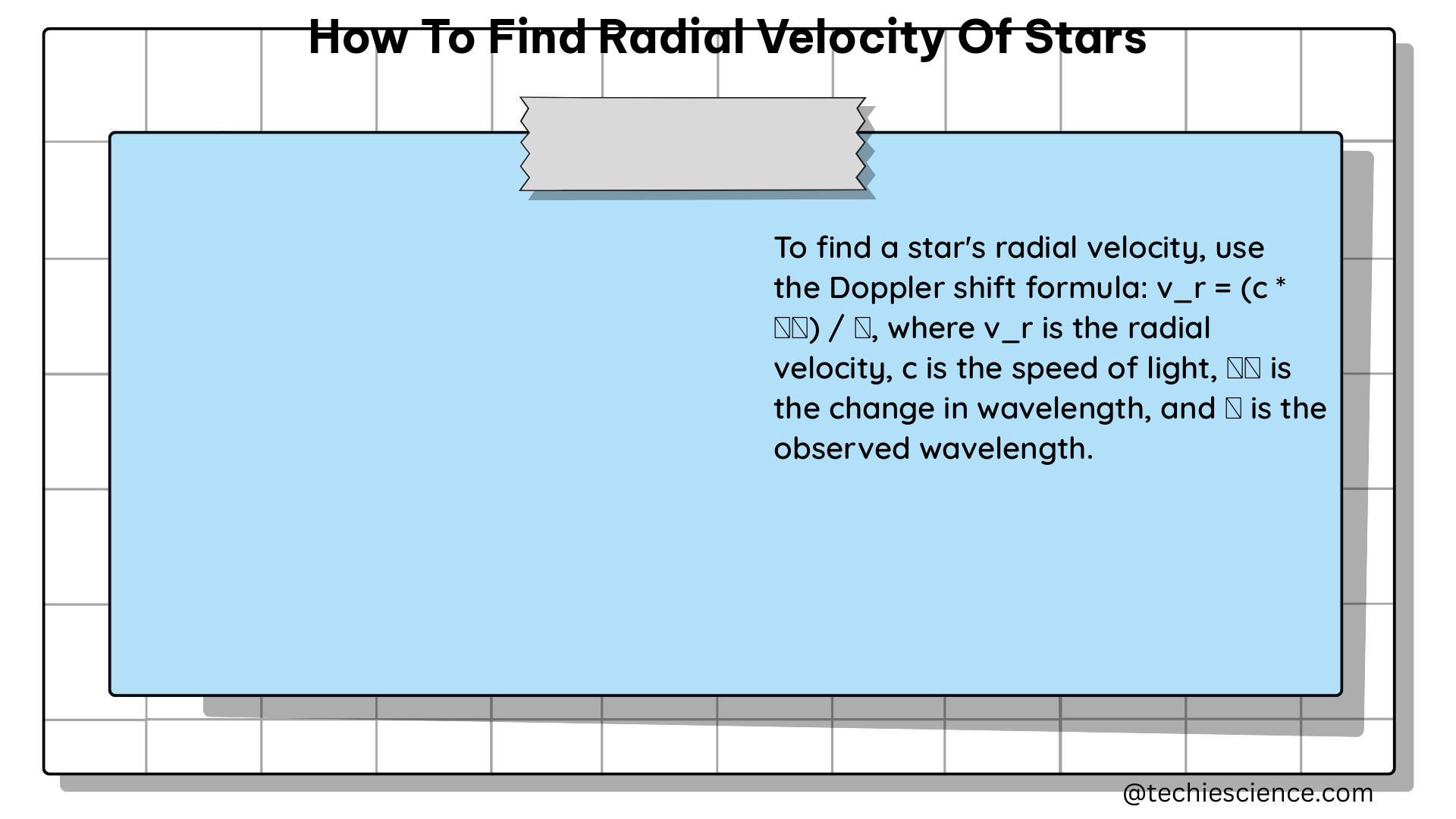
The relationship between the observed wavelength shift (Δλ), the rest wavelength (λ₀), the radial velocity (vᵣ), and the speed of light (c) is given by the Doppler shift formula:

Δλ / λ₀ = vᵣ / c

This formula allows us to calculate the radial velocity of a star based on the observed wavelength shift of its spectral lines.

Measuring the Wavelength Shift

To measure the radial velocity of a star, we need to accurately determine the wavelength shift of its spectral lines. This process involves the following steps:

1. Obtaining the Star’s Spectrum: Using a high-resolution spectrograph, we can capture the spectrum of the target star, which displays the characteristic absorption lines corresponding to the elements present in the star’s atmosphere.

2. Identifying Spectral Lines: Carefully examine the star’s spectrum and identify the specific spectral lines that will be used for the radial velocity measurement. These lines should be well-defined and unblended.

3. Measuring the Wavelength Shift: Compare the observed wavelength of the selected spectral lines in the star’s spectrum to their known rest wavelengths, which are typically obtained from laboratory measurements. The difference between the observed and rest wavelengths is the wavelength shift (Δλ).

4. Calculating the Radial Velocity: Plug the measured wavelength shift (Δλ), the rest wavelength (λ₀), and the speed of light (c) into the Doppler shift formula to calculate the radial velocity (vᵣ) of the star.

Factors Affecting Radial Velocity Measurements

Accurate radial velocity measurements require careful consideration of various factors that can influence the observed wavelength shifts. Some of these factors include:

1. Stellar Rotation: The rotation of the star can cause Doppler shifts in different parts of the star’s surface, leading to line broadening and potential blending of spectral lines.

2. Stellar Pulsations: Some stars exhibit periodic pulsations, which can introduce additional Doppler shifts in their spectra.

3. Stellar Convection: Convective motions within the star’s atmosphere can also contribute to Doppler shifts in the observed spectral lines.

4. Gravitational Redshift: The gravitational field of the star can cause a small redshift in the observed wavelengths, known as the gravitational redshift.

5. Instrumental Effects: Factors such as the stability and calibration of the spectrograph, as well as the resolution and signal-to-noise ratio of the observations, can all impact the accuracy of the radial velocity measurements.

To account for these factors and obtain reliable radial velocity measurements, astronomers employ various techniques, including high-resolution spectroscopy, precise wavelength calibration, and advanced data analysis methods.

Radial Velocity Measurement Techniques

Several techniques have been developed to measure the radial velocity of stars with high precision. Some of the most commonly used methods include:

1. Cross-Correlation Technique: This method involves cross-correlating the observed stellar spectrum with a template spectrum, typically from a reference star or a synthetic spectrum. The shift in the cross-correlation function peak corresponds to the radial velocity of the target star.

2. Least-Squares Deconvolution: This technique uses the information from multiple spectral lines to derive a high-resolution, high signal-to-noise ratio “mean” line profile, which is then used to measure the radial velocity.

3. Iodine Cell Technique: In this method, an iodine absorption cell is placed in the optical path of the spectrograph, introducing a set of well-known absorption lines that can be used as a wavelength reference for the radial velocity measurement.

4. Laser Frequency Comb Technique: Laser frequency combs provide an extremely stable and precise wavelength reference, enabling highly accurate radial velocity measurements by calibrating the spectrograph’s wavelength scale.

5. Doppler Imaging: This technique combines high-resolution spectroscopy with Doppler tomography to reconstruct the surface features and velocity fields of rapidly rotating stars, providing insights into their radial velocity variations.

Each of these techniques has its own advantages, limitations, and specific applications, depending on the characteristics of the target star and the available instrumentation.

Practical Considerations and Challenges

Measuring the radial velocity of stars is not without its challenges. Some practical considerations and challenges include:

1. Spectral Line Identification: Accurately identifying the spectral lines in the star’s spectrum, especially when they are significantly shifted from their rest wavelengths, can be a complex and time-consuming task.

2. Blended Spectral Lines: In some cases, spectral lines may be blended or overlapping, making it difficult to accurately measure the wavelength shift and derive the radial velocity.

3. Faint or Low Signal-to-Noise Spectra: Observing faint stars or those with low signal-to-noise ratios can limit the precision of the radial velocity measurements.

4. Stellar Activity and Variability: Phenomena such as stellar pulsations, convection, and magnetic activity can introduce additional Doppler shifts, complicating the interpretation of the radial velocity measurements.

5. Instrumental Stability and Calibration: Maintaining the stability and accurate calibration of the spectrograph is crucial for obtaining reliable radial velocity measurements over extended periods.

Overcoming these challenges often requires the use of advanced data analysis techniques, sophisticated instrumentation, and a deep understanding of stellar astrophysics.

Applications of Radial Velocity Measurements

Radial velocity measurements have a wide range of applications in astronomy and astrophysics, including:

1. Exoplanet Detection: The radial velocity method is one of the most successful techniques for detecting and characterizing exoplanets, as the presence of a planet orbiting a star can be inferred from the periodic variations in the star’s radial velocity.

2. Stellar Dynamics and Galactic Structure: Radial velocity data, combined with proper motion measurements, can provide insights into the dynamics of stellar systems, the structure of our Milky Way galaxy, and the overall motion of stars within the galaxy.

3. Stellar Astrophysics: Radial velocity measurements can be used to study the physical properties and evolution of stars, such as their masses, sizes, and internal structures.

4. Cosmology and Extragalactic Astronomy: Radial velocity measurements of distant galaxies and quasars are crucial for understanding the large-scale structure and expansion of the universe, as well as the properties of active galactic nuclei.

5. Asteroseismology: Radial velocity variations can be used to study the internal structure and oscillations of stars, providing valuable information about their age, composition, and evolutionary state.

As technology and observational techniques continue to advance, the precision and applications of radial velocity measurements are expected to expand, further enhancing our understanding of the universe and the celestial bodies that inhabit it.

Conclusion

Measuring the radial velocity of stars is a fundamental technique in observational astronomy, with a wide range of applications and significant scientific impact. By understanding the Doppler shift, mastering the measurement process, and addressing the various factors and challenges involved, astronomers can obtain reliable and high-precision radial velocity data that contribute to our knowledge of stellar systems, exoplanets, galactic structure, and the evolution of the universe. This comprehensive guide has provided a detailed overview of the technical aspects and practical considerations in finding the radial velocity of stars, equipping you with the necessary knowledge to embark on your own stellar velocity investigations.

References

1. Radial Velocity | Exoplanets. (n.d.). Retrieved from http://exoplanets.astro.yale.edu/workshop/EPRV/Bibliography_files/Radial_Velocity.pdf
2. Stellar Velocities | Astronomy 801 – Dutton Institute – Penn State. (n.d.). Retrieved from https://www.e-education.psu.edu/astro801/content/l4_p7.html
3. QUANTIFYING THE EVIDENCE FOR A PLANET IN RADIAL VELOCITY – YouTube. (n.d.). Retrieved from https://www.youtube.com/watch?v=cVKSzBbAZxw
4. Trifonov, T., Tal-Or, L., Zechmeister, M., Kaminski, A., Zucker, S., & Mazeh, T. (2019). Measuring precise radial velocities and cross-correlation function line-profile variations using a Skew Normal density. Astronomy & Astrophysics, 623, A16. https://doi.org/10.1051/0004-6361/201833153