Mastering the Art of Finding Power with Volts and Amps: A Comprehensive Guide

Calculating power in electrical circuits is a fundamental skill for any physics student or electrical engineer. By understanding the relationship between voltage, current, and power, you can accurately determine the power consumption of various electrical devices and systems. In this comprehensive guide, we will delve into the intricacies of finding power using volts and amps, providing you with a thorough understanding of the underlying principles and practical applications.

Understanding the Power Formula

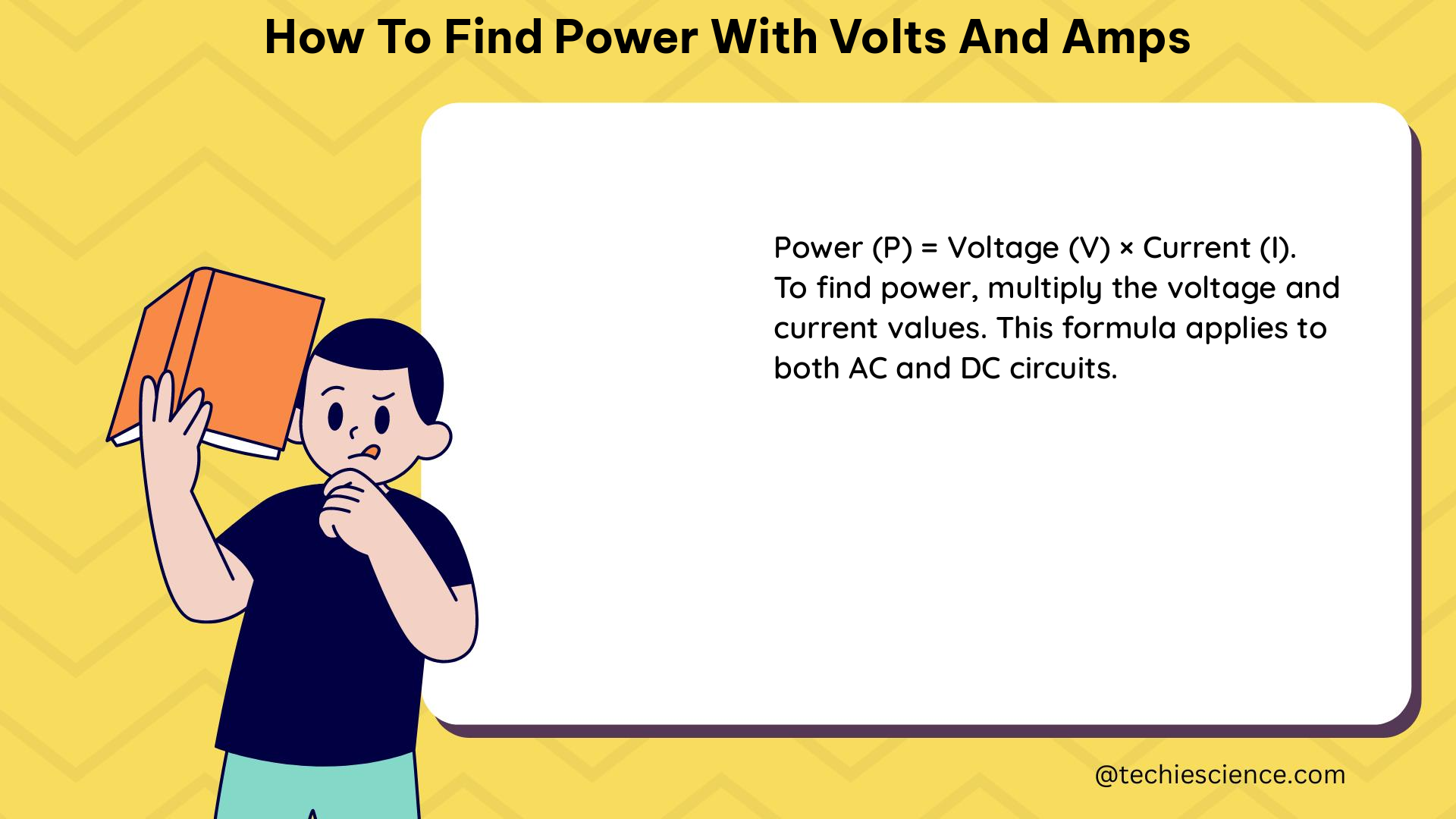
The basic formula for calculating power (P) in an electrical circuit is:

P = V × I

Where:
– P is the power in watts (W)
– V is the voltage in volts (V)
– I is the current in amperes (A)

This formula is applicable to resistive loads, where the current and voltage are in phase. However, for inductive or capacitive loads, such as motors or transformers, the power factor must be considered to account for the phase difference between current and voltage.

Calculating Power Factor

The power factor (PF) is a measure of how effectively electrical power is being used. It is calculated by dividing the total watts from each meter by the total volt-amps. The power factor can range from 0 to 1, with 1 indicating that the power is being used most efficiently.

The formula for calculating power factor is:

PF = P / (V × I)

Where:
– PF is the power factor (dimensionless)
– P is the power in watts (W)
– V is the voltage in volts (V)
– I is the current in amperes (A)

Understanding the power factor is crucial when dealing with non-resistive loads, as it can significantly impact the overall power consumption and efficiency of the system.

Measuring Power in Different Circuit Configurations

The number of wattmeters required to measure power in a circuit depends on the circuit configuration:

1. Single-phase, two-wire system: One wattmeter is required.
2. Single-phase, three-wire system: Two wattmeters are required.
3. Three-phase, three-wire system: Two wattmeters are required.
4. Three-phase, four-wire system: Three wattmeters are required.

It’s important to note that the placement and connection of the wattmeters are crucial for accurate power measurements.

Power Measurement Instruments

Power is typically measured using digital power analyzers or digital storage oscilloscopes (DSOs) with power-analysis firmware. These instruments provide accurate and reliable power measurements.

Digital Power Analyzers

Digital power analyzers can directly measure up to 50 A RMS at voltage levels up to 1000 V RMS, making them suitable for a wide range of applications. They provide true power measurements by analyzing the digitized waveforms.

Digital Storage Oscilloscopes (DSOs) with Power-Analysis Firmware

DSOs with power-analysis firmware can also be used to measure power. These instruments rely on sample data from digitized waveforms, which may not provide the same level of accuracy as a dedicated power analyzer. However, they can be a more cost-effective solution for certain applications.

Converting Amps to Volts Using Watts

In some cases, you may need to convert amps to volts using the known power (watts) in a circuit. The formula for this conversion is:

V = P / I

Where:
– V is the voltage in volts (V)
– P is the power in watts (W)
– I is the current in amperes (A)

This formula is applicable to resistive loads. For inductive or capacitive loads, such as motors or transformers, the power factor must be considered to ensure accurate voltage calculations.

Practical Examples and Numerical Problems

Let’s explore some practical examples and numerical problems to solidify your understanding of finding power with volts and amps.

Example 1: Calculating Power in a Resistive Load

Suppose you have a resistive load with a voltage of 120 V and a current of 5 A. Calculate the power consumed by the load.

Given:
– Voltage (V) = 120 V
– Current (I) = 5 A

Using the power formula:
P = V × I
P = 120 V × 5 A
P = 600 W

Therefore, the power consumed by the resistive load is 600 watts.

Example 2: Calculating Power Factor and Power in an Inductive Load

Consider an inductive load with a voltage of 240 V, a current of 10 A, and a power factor of 0.8.

Given:
– Voltage (V) = 240 V
– Current (I) = 10 A
– Power Factor (PF) = 0.8

Step 1: Calculate the apparent power (S)
S = V × I
S = 240 V × 10 A
S = 2400 VA

Step 2: Calculate the real power (P)
P = V × I × PF
P = 240 V × 10 A × 0.8
P = 1920 W

Therefore, the power consumed by the inductive load is 1920 watts, and the power factor is 0.8.

Numerical Problem 1

A resistive load has a voltage of 220 V and a current of 2.5 A. Calculate the power consumed by the load.

Numerical Problem 2

An inductive load has a voltage of 380 V, a current of 15 A, and a power factor of 0.9. Calculate the real power and apparent power consumed by the load.

By working through these examples and numerical problems, you will develop a deeper understanding of the concepts and techniques involved in finding power with volts and amps.

Conclusion

In this comprehensive guide, we have explored the fundamental principles and practical applications of finding power with volts and amps. From understanding the power formula to calculating power factor and measuring power in different circuit configurations, you now have a solid foundation to tackle power-related problems in electrical circuits.

Remember, the key to mastering this topic lies in practicing the concepts and applying them to real-world scenarios. Continuously challenge yourself with new examples and numerical problems to solidify your knowledge and become a true expert in the field of electrical power calculations.

Reference:

1. Electricity Basics for Data Centers
2. Watts, Amps, and Volts Calculators
3. Ultimate Guide to Amps, Watts, and Volts
4. How to Measure Electrical Power
5. Amps to Volts Calculator