In the world of electrical circuits, understanding the relationship between power, resistance, and voltage is crucial for effective analysis and design. This comprehensive guide will delve into the fundamental principles, formulas, and practical examples to help you master the art of finding power with resistance and voltage.
Ohm’s Law and the Power Formula
The foundation of this topic lies in Ohm’s Law and the power formula. Ohm’s Law states that the voltage (E) across a resistor is directly proportional to the current (I) flowing through it, and the constant of proportionality is the resistance (R). This relationship can be expressed as:
E = I × R
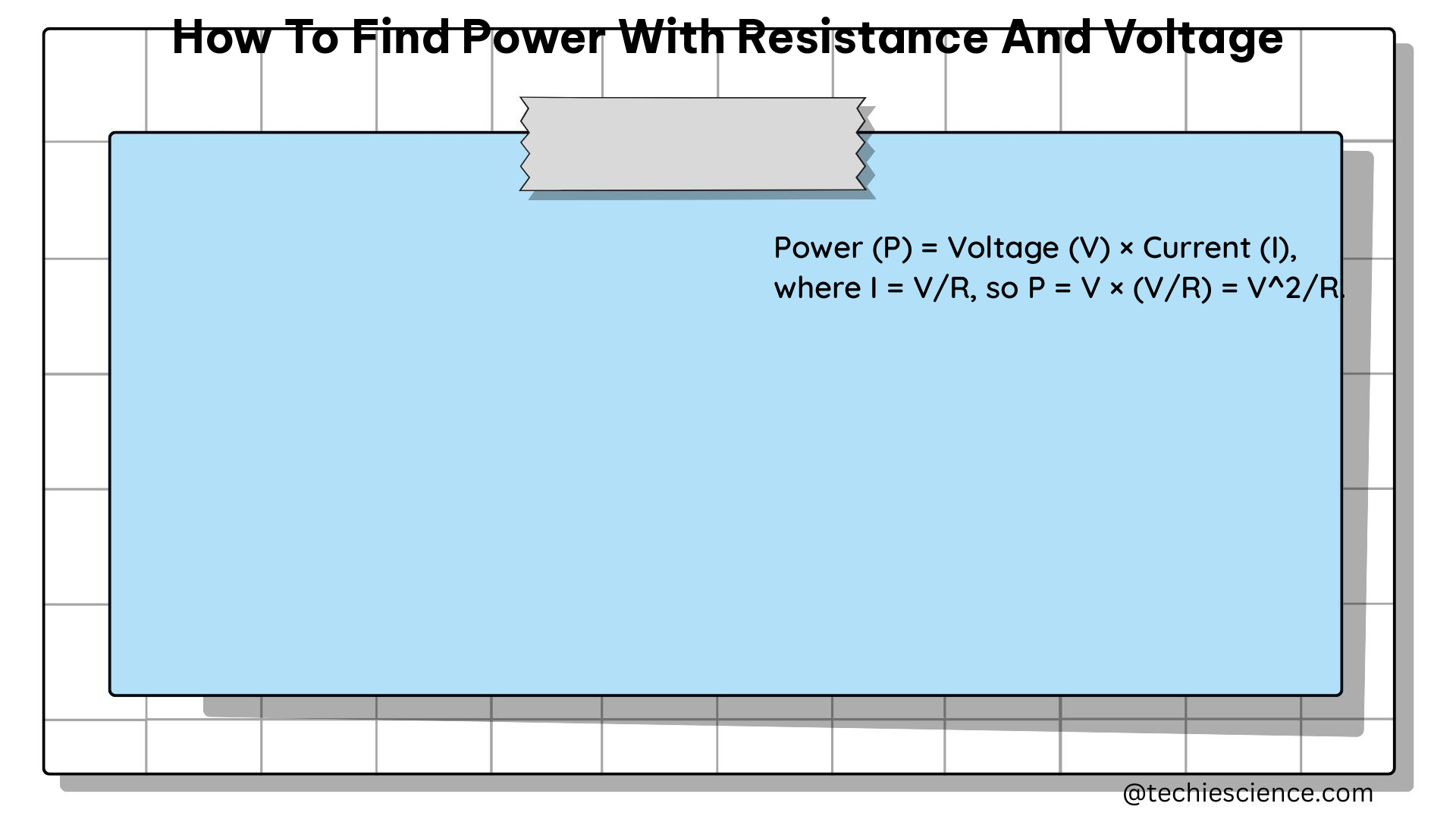
The power formula, on the other hand, describes the rate at which energy is transferred or transformed in an electrical circuit. The power (P) can be calculated using one of the following formulas:
P = V × I
P = V^2 / R
P = I^2 × R
Where:
– P is the power in watts (W)
– V is the voltage in volts (V)
– I is the current in amperes (A)
– R is the resistance in ohms (Ω)
Understanding these fundamental relationships is crucial for finding power with resistance and voltage.
Physics Examples
Let’s explore some practical examples to solidify our understanding.
Example 1: Calculating Power with Voltage and Resistance
Suppose we have a circuit with a voltage of 12 volts and a resistance of 4 ohms. To find the power, we can use the formula:
P = V^2 / R
P = (12 V)^2 / 4 Ω
P = 144 W / 4 Ω
P = 36 watts
Example 2: Calculating Power with Current and Resistance
Now, let’s consider a circuit with a current of 3 amperes and a resistance of 6 ohms. We can use the formula:
P = I^2 × R
P = (3 A)^2 × 6 Ω
P = 9 A^2 × 6 Ω
P = 54 watts
These examples demonstrate how to apply the power formula using either voltage and resistance or current and resistance to find the power in a circuit.
Physics Numerical Problems
Now, let’s put your understanding to the test with some numerical problems.
Problem 1
A circuit has a voltage of 20 volts and a resistance of 10 ohms. What is the power?
Problem 2
A circuit has a current of 5 amperes and a resistance of 2 ohms. What is the power?
Problem 3
A circuit has a voltage of 15 volts and a current of 4 amperes. What is the power?
Remember to show your work and use the appropriate power formula to solve these problems.
Figures and Diagrams
To further enhance your understanding, let’s explore some visual aids.
Figure 1: Ohm’s Law Triangle
The Ohm’s Law triangle is a useful tool for remembering the relationships between voltage, current, and resistance. It can be used to quickly determine the unknown quantity when the other two are known.
Figure 2: Circuit Diagram with Resistors and Voltage Sources
A simple circuit diagram can help you visualize the components and their connections, making it easier to apply the power formula and solve problems.
Data Points, Values, and Measurements
To provide a comprehensive reference, let’s compile a table of relevant data points, values, and measurements:
| Parameter | Values |
|---|---|
| Voltage (V) | 10 V, 12 V, 20 V, 15 V |
| Current (I) | 2 A, 3 A, 5 A, 4 A |
| Resistance (R) | 5 Ω, 4 Ω, 6 Ω, 10 Ω, 2 Ω |
| Power (P) | 20 W, 36 W, 54 W, varying |
This table can serve as a quick reference for the values used in the examples and problems presented earlier.
Reference Links
For further exploration and deeper understanding, here are some recommended reference links:
- Ohm’s Law – How Voltage, Current, and Resistance Relate: https://www.allaboutcircuits.com/textbook/direct-current/chpt-2/voltage-current-resistance-relate/
- Current, voltage and resistance – Primary Connections: https://www.primaryconnections.org.au/themes/custom/connections/assets/SBR/data/Phy/sub/current/current.htm
- Calculate Current (Amps) with Ohm’s Law and the Power Formula: https://www.elliottelectric.com/StaticPages/ElectricalReferences/Calculations/Ohms_Law_Calculating.aspx
By mastering the concepts presented in this comprehensive guide, you will be well-equipped to tackle a wide range of problems involving power, resistance, and voltage in electrical circuits. Remember to practice regularly and apply the principles to solidify your understanding.

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.