How to Find Power with Mass, Distance, and Time: A Comprehensive Guide

In the realm of physics, understanding the relationship between mass, distance, and time is crucial for calculating power, a fundamental concept that underpins many physical phenomena. This comprehensive guide will delve into the formulas, examples, and theoretical explanations to help you master the art of finding power using these key variables.

Work (W)

The first step in calculating power is to determine the work done. Work is defined as the product of the force (F) and the distance (d) moved in the direction of the force. The formula for work is:

[
W = F \times d
]

For a mass (m) lifted against gravity, the force is given by:

[
F = m \times g
]

where g is the acceleration due to gravity, approximately 9.81 m/s².

Power (P)

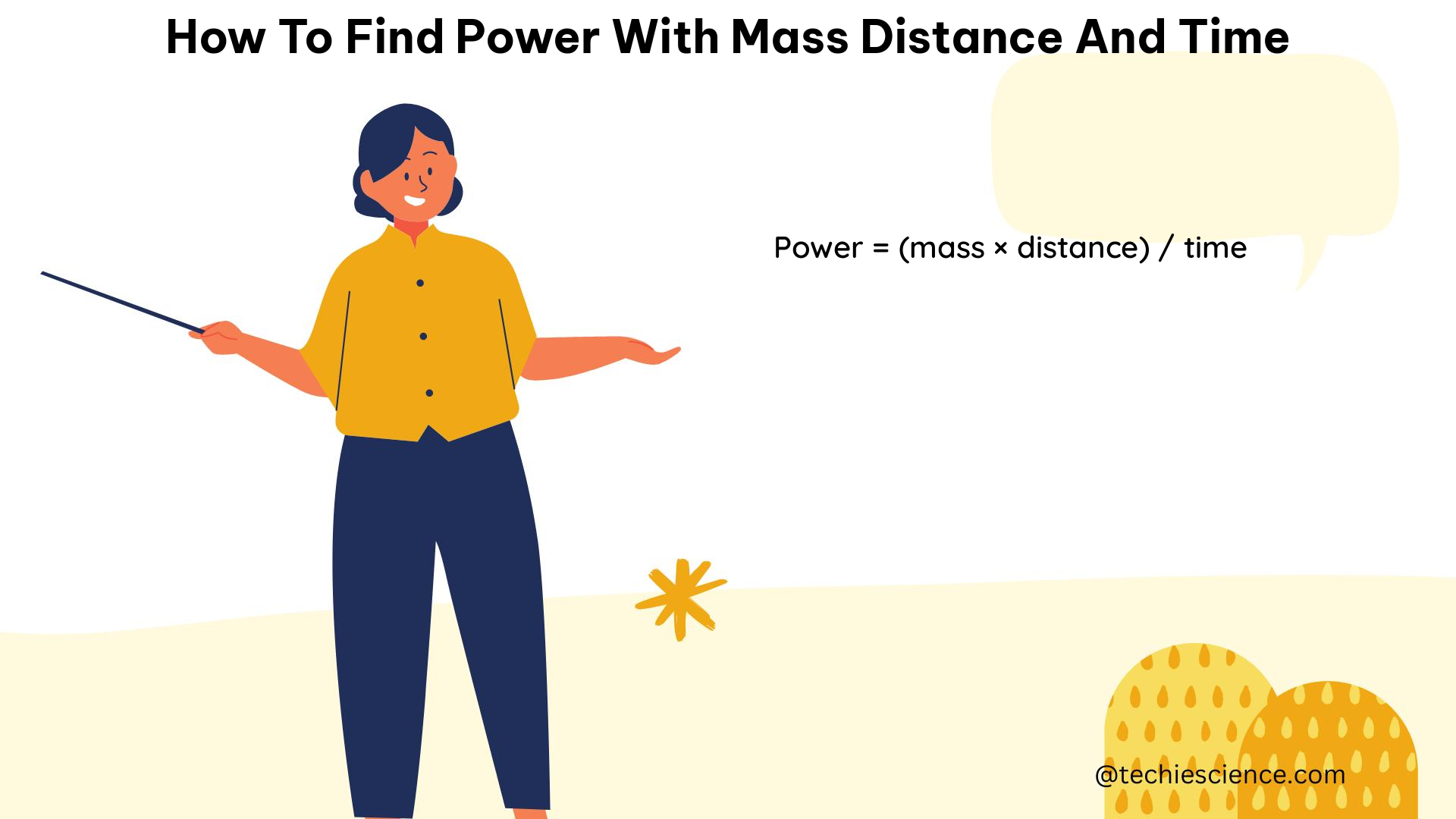
Power is a measure of the rate at which work is done. It is calculated by dividing the work done by the time taken to do that work. The formula for power is:

[
P = \frac{W}{t}
]

Alternatively, you can calculate power directly using the force and velocity (v):

[
P = F \times v
]

Example Problem

Let’s consider a scenario where a weightlifter lifts a 50 kg barbell a distance of 1.2 m in 1.5 seconds. We can use the formulas to calculate the power expended.

1. Work (W):
2. Calculate the force:
   [
   F = 50 \text{ kg} \times 9.81 \text{ m/s}^2 = 490.5 \text{ N}
   ]

3. Calculate the work:
   [
   W = 490.5 \text{ N} \times 1.2 \text{ m} = 588.6 \text{ J}
   ]

4. Power (P):

5. Calculate the power:
   [
   P = \frac{588.6 \text{ J}}{1.5 \text{ s}} = 392.4 \text{ W}
   ]

Theoretical Explanation

Power is a fundamental concept in physics that represents the rate at which work is done. It is the measure of the amount of energy transferred or the rate of doing work. The power formula, P = W/t, shows that power is directly proportional to the work done and inversely proportional to the time taken to do the work.

The work done is the product of the force applied and the distance moved in the direction of the force. For a mass lifted against gravity, the force is given by the product of the mass and the acceleration due to gravity. This relationship allows us to calculate the work done and, subsequently, the power expended.

Figures and Data Points

• Force (F): 490.5 N
• Distance (d): 1.2 m
• Time (t): 1.5 s
• Work (W): 588.6 J
• Power (P): 392.4 W

Measurements and Units

• Force: Newtons (N)
• Distance: Meters (m)
• Time: Seconds (s)
• Work: Joules (J)
• Power: Watts (W)

References

1. Physics Forums: Given mass, distance, and time, calculate power
2. Dummies.com: How to Calculate Power Based on Force and Speed
3. Find Tutors: How can I calculate work, energy, and power?

By understanding the formulas, examples, and theoretical explanations provided in this guide, you will be well-equipped to tackle problems involving the calculation of power using mass, distance, and time. Remember, practice and a deep understanding of the underlying physics principles are key to mastering this topic.