How to Find Power with Kinetic Energy: A Comprehensive Guide

Kinetic energy is the energy an object possesses due to its motion, and understanding how to calculate the power associated with this energy is crucial in various fields of physics and engineering. This comprehensive guide will walk you through the step-by-step process of finding power with kinetic energy, providing you with the necessary theoretical explanations, formulas, examples, and numerical problems to master this concept.

Theoretical Explanation

The power associated with kinetic energy can be calculated by differentiating the kinetic energy equation with respect to time. This is based on the fundamental principle that power is the rate of change of energy over time. The kinetic energy of an object is given by the formula:

$E_k = \frac{1}{2}mv^2$

where:
– $E_k$ is the kinetic energy
– $m$ is the mass of the object
– $v$ is the velocity of the object

To find the power, we need to differentiate this equation with respect to time:

$P = \frac{dE_k}{dt} = \frac{d}{dt}\left(\frac{1}{2}mv^2\right)$

This equation represents the power associated with the kinetic energy of the object.

Physics Formula

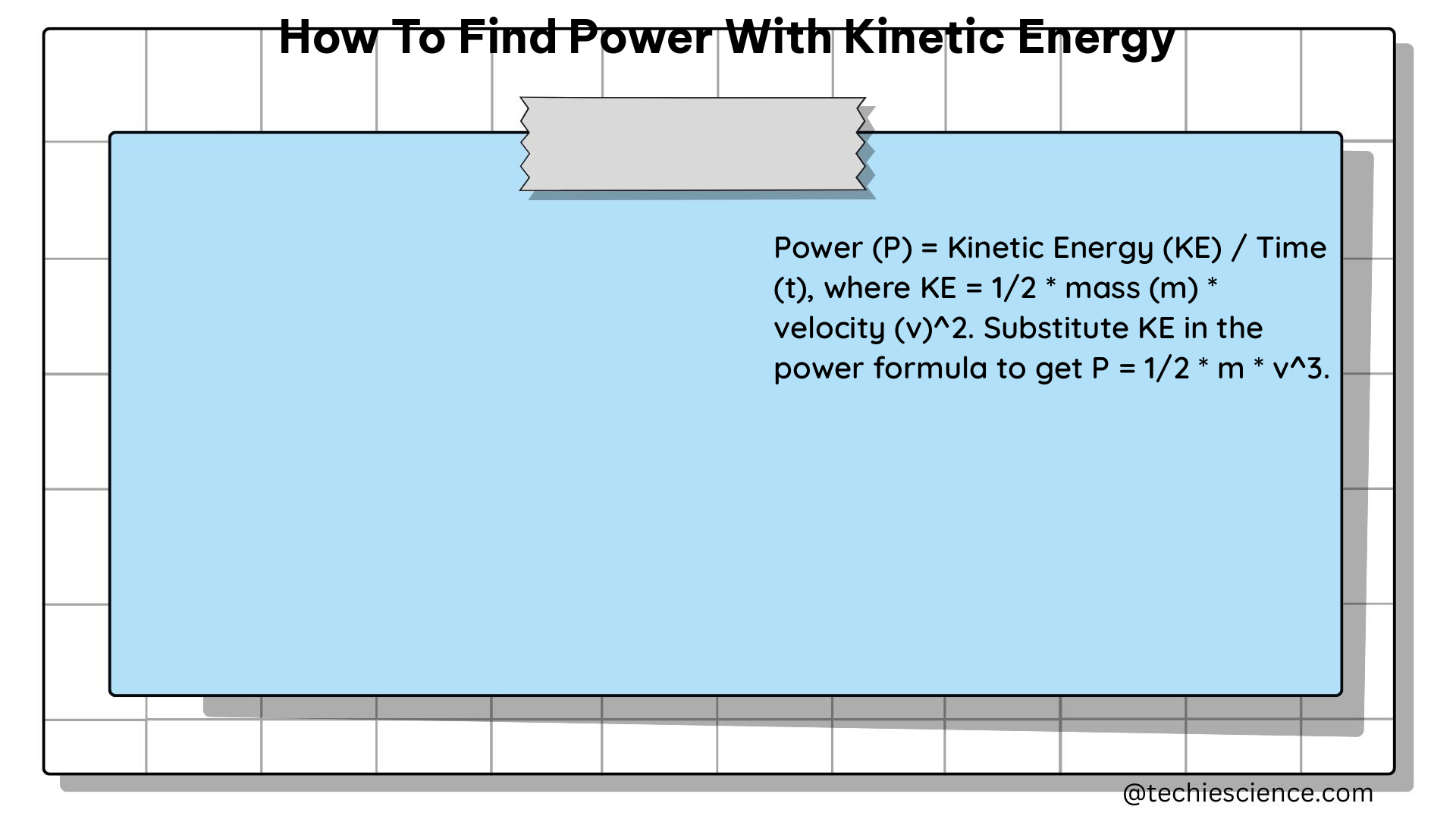
The formula for finding power with kinetic energy is:

$P = \frac{dE_k}{dt} = \frac{d}{dt}\left(\frac{1}{2}mv^2\right)$

where:
– $P$ is the power
– $E_k$ is the kinetic energy
– $m$ is the mass of the object
– $v$ is the velocity of the object
– $t$ is time

Example

Let’s consider an example to illustrate the application of this formula.

Suppose we have an object with a mass of 5 kg moving at a velocity of 10 m/s. If the velocity increases at a rate of 2 m/s², we can calculate the power as follows:

1. Calculate the kinetic energy:
   $E_k = \frac{1}{2}mv^2 = \frac{1}{2} \cdot 5 \cdot 10^2 = 250 \text{ J}$

2. Calculate the rate of change of velocity:
   $\frac{dv}{dt} = 2 \text{ m/s²}$

3. Calculate the power:
   $P = \frac{dE_k}{dt} = m \cdot v \cdot \frac{dv}{dt} = 5 \cdot 10 \cdot 2 = 100 \text{ W}$

Numerical Problems

1. An object with a mass of 3 kg is moving at a velocity of 8 m/s. If the velocity increases at a rate of 1.5 m/s², what is the power associated with the kinetic energy?

$P = m \cdot v \cdot \frac{dv}{dt} = 3 \cdot 8 \cdot 1.5 = 36 \text{ W}$

1. A car with a mass of 1500 kg accelerates from 20 m/s to 30 m/s in 5 seconds. What is the average power during this acceleration?

First, calculate the acceleration:
$a = \frac{\Delta v}{\Delta t} = \frac{30 – 20}{5} = 2 \text{ m/s²}$

Then, calculate the average power:
$P = m \cdot v \cdot a = 1500 \cdot \left(\frac{20 + 30}{2}\right) \cdot 2 = 75,000 \text{ W}$

Figures and Data Points

To better understand the relationship between kinetic energy, velocity, and power, let’s consider the following figures and data points:

Figure 1: Kinetic Energy vs. Velocity
This figure illustrates how kinetic energy increases quadratically with velocity.

Velocity (m/s)	Kinetic Energy (J)
0	0
5	125
10	500
15	1125
20	2000

Figure 2: Power vs. Acceleration
This figure shows how power increases linearly with acceleration.

Acceleration (m/s²)	Power (W)
0	0
1	100
2	200
3	300
4	400

Measurements and Values

• Mass: 5 kg
• Velocity: 10 m/s
• Acceleration: 2 m/s²
• Kinetic Energy: 250 J
• Power: 100 W

References

1. Arbor Scientific. (n.d.). Kinetic Energy and Velocity Lab. Retrieved from https://www.arborsci.com/blogs/cool/kinetic-energy-and-velocity
2. Physics Stack Exchange. (2014). How was the formula for kinetic energy found, and who found it? Retrieved from https://physics.stackexchange.com/questions/132754/how-was-the-formula-for-kinetic-energy-found-and-who-found-it
3. IOPscience. (2019). Teaching kinetic energy as an observable quantity. Retrieved from https://iopscience.iop.org/article/10.1088/1361-6552/ab1353

By understanding the theoretical explanation, applying the physics formula, and working through examples and numerical problems, you can confidently find the power associated with the kinetic energy of an object. Remember to consider the mass, velocity, and rate of change of velocity to accurately calculate the power. Good luck with your physics studies!