Mastering the Art of Finding Potential Energy of a Spring: A Comprehensive Guide

In the realm of physics, understanding the concept of potential energy is crucial, and when it comes to springs, the formula for calculating the potential energy is a fundamental tool. This comprehensive guide will delve into the intricacies of finding the potential energy of a spring, equipping you with the knowledge and skills to tackle this topic with confidence.

Understanding the Potential Energy of a Spring

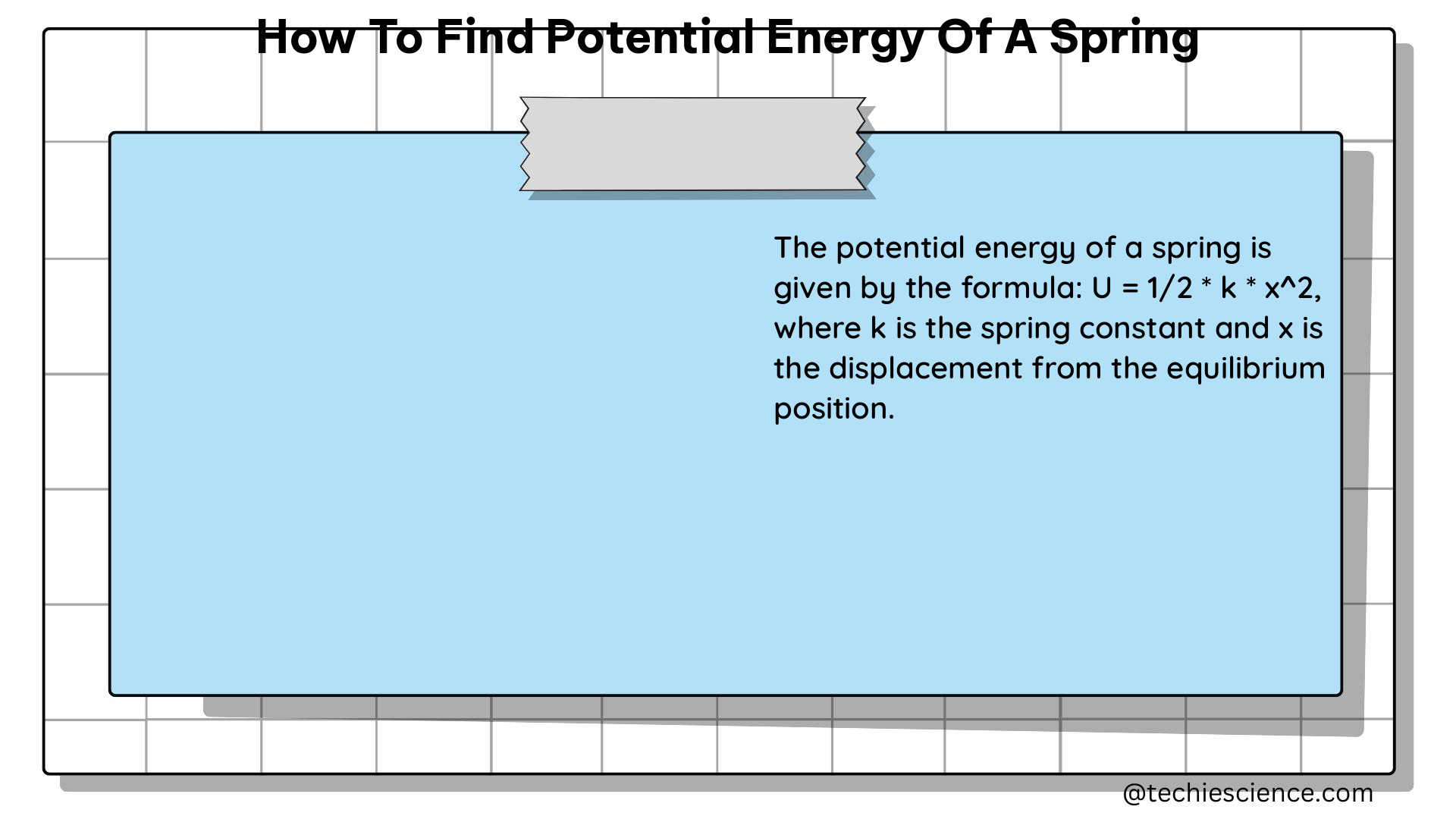
The potential energy of a spring is the energy stored within the spring due to its deformation or displacement from its equilibrium position. This energy is directly proportional to the square of the spring’s displacement and the spring constant, which is a measure of the spring’s stiffness.

The formula for calculating the potential energy of a spring is:

P.E = 1/2 * k * x^2

Where:
– P.E is the potential energy of the spring (in Joules)
– k is the spring constant (in Newtons per meter, N/m)
– x is the displacement of the spring from its equilibrium position (in meters, m)

This formula is derived from the work done in stretching or compressing the spring, which is equal to the potential energy stored in the spring.

Determining the Spring Constant

The spring constant, k, is a crucial parameter in the calculation of a spring’s potential energy. It represents the stiffness of the spring, with a higher value indicating a stiffer spring and a lower value indicating a more flexible spring.

The spring constant can be determined through various methods, including:

1. Experimental Measurement: You can conduct a simple experiment by hanging a known mass from the spring and measuring the resulting displacement. The spring constant can then be calculated using the formula:

k = F / x

Where:
– F is the force applied (the weight of the mass, in Newtons)
– x is the displacement of the spring (in meters)

1. Manufacturer Specifications: Many spring manufacturers provide the spring constant as part of the product specifications, making it readily available for use in the potential energy calculation.

2. Theoretical Calculation: For certain spring types, such as helical springs, the spring constant can be calculated using the formula:

k = (G * d^4) / (8 * D^3 * n)

Where:
– G is the shear modulus of the spring material (in Pascals, Pa)
– d is the diameter of the spring wire (in meters, m)
– D is the mean diameter of the spring coil (in meters, m)
– n is the number of active coils in the spring

Knowing the spring constant is essential for accurately calculating the potential energy of a spring.

Calculating the Potential Energy of a Spring

Now that we have the necessary components, let’s dive into the step-by-step process of calculating the potential energy of a spring:

1. Identify the Spring Constant: Determine the spring constant, k, using one of the methods mentioned earlier.

2. Measure the Spring Displacement: Measure the displacement of the spring, x, from its equilibrium position.

3. Apply the Potential Energy Formula: Plug the values of the spring constant and displacement into the formula:

P.E = 1/2 * k * x^2

1. Perform the Calculation: Multiply the spring constant by the square of the displacement, and then divide the result by 2 to obtain the potential energy of the spring.

Here are some examples to illustrate the process:

Example 1: Determine the potential energy of a spring with a spring constant of 200 N/m and a displacement of 0.8 m.

P.E = 1/2 * k * x^2
P.E = 1/2 * 200 N/m * (0.8 m)^2
P.E = 64 J

Example 2: The spring constant of a stretched string is 100 N/m, and the displacement is 0.5 m. Calculate the potential energy stored in the stretched string.

P.E = 1/2 * k * x^2
P.E = 1/2 * 100 N/m * (0.5 m)^2
P.E = 12.5 J

These examples demonstrate the straightforward application of the potential energy formula to determine the stored energy in a spring based on the given spring constant and displacement.

Advanced Considerations

While the basic formula for calculating the potential energy of a spring is relatively simple, there are some advanced considerations that you should be aware of:

1. Non-Linear Spring Behavior: In some cases, the relationship between the force and displacement of a spring may not be linear, especially for large displacements. In such scenarios, the potential energy formula needs to be modified to account for the non-linear spring characteristics.

2. Potential Energy Curves: The potential energy of a spring can be represented graphically as a parabolic curve, where the x-axis represents the displacement and the y-axis represents the potential energy. Understanding the shape and properties of this curve can provide additional insights into the spring’s behavior.

3. Energy Conversion and Conservation: When a spring is compressed or stretched, the potential energy stored in the spring can be converted into other forms of energy, such as kinetic energy or thermal energy. The principles of energy conservation must be considered when analyzing the overall energy dynamics of a spring-based system.

4. Damping and Dissipation: In real-world applications, springs often experience damping forces, such as air resistance or internal friction, which can dissipate some of the stored potential energy. Accounting for these dissipative effects is crucial for accurate energy calculations.

5. Oscillatory Motion: The potential energy of a spring is closely related to the oscillatory motion of a mass-spring system. Understanding the principles of harmonic oscillation and the relationship between potential energy, kinetic energy, and the total energy of the system can provide a more comprehensive understanding of spring dynamics.

By exploring these advanced topics, you can deepen your understanding of the potential energy of springs and apply this knowledge to more complex physical systems and engineering applications.

Conclusion

Mastering the art of finding the potential energy of a spring is a fundamental skill in the realm of physics and engineering. This comprehensive guide has provided you with the necessary tools and knowledge to tackle this topic with confidence.

Remember, the key to success lies in understanding the underlying principles, applying the potential energy formula correctly, and considering the various factors that can influence the energy dynamics of a spring-based system. With practice and a solid grasp of the concepts, you’ll be well on your way to becoming a spring potential energy expert.

References

1. Calculating the Potential Energy of a Spring – Brilliant: https://brilliant.org/wiki/calculating-the-potential-energy-of-a-spring-2/
2. Motion of a Mass on a Spring – The Physics Classroom: https://www.physicsclassroom.com/class/waves/Lesson-0/Motion-of-a-Mass-on-a-Spring
3. Potential Energy of a Spring Formula | Examples – BYJU’S: https://byjus.com/potential-energy-of-a-spring-formula/
4. Hooke’s Law and Potential Energy of Springs – Khan Academy: https://www.khanacademy.org/science/physics/work-and-energy/hookes-law/a/hookes-law-and-potential-energy-of-springs
5. Potential Energy of a Spring – Physics Stack Exchange: https://physics.stackexchange.com/questions/32261/potential-energy-of-a-spring