How to Find Orbital Velocity of Satellites: A Comprehensive Guide

The orbital velocity of a satellite is the speed at which it revolves around a celestial body, such as a planet or a star. This velocity is crucial for maintaining the satellite’s orbit and ensuring its stability. In this comprehensive guide, we will delve into the intricacies of calculating the orbital velocity of satellites, providing you with a thorough understanding of the underlying principles and practical applications.

Understanding the Orbital Velocity Formula

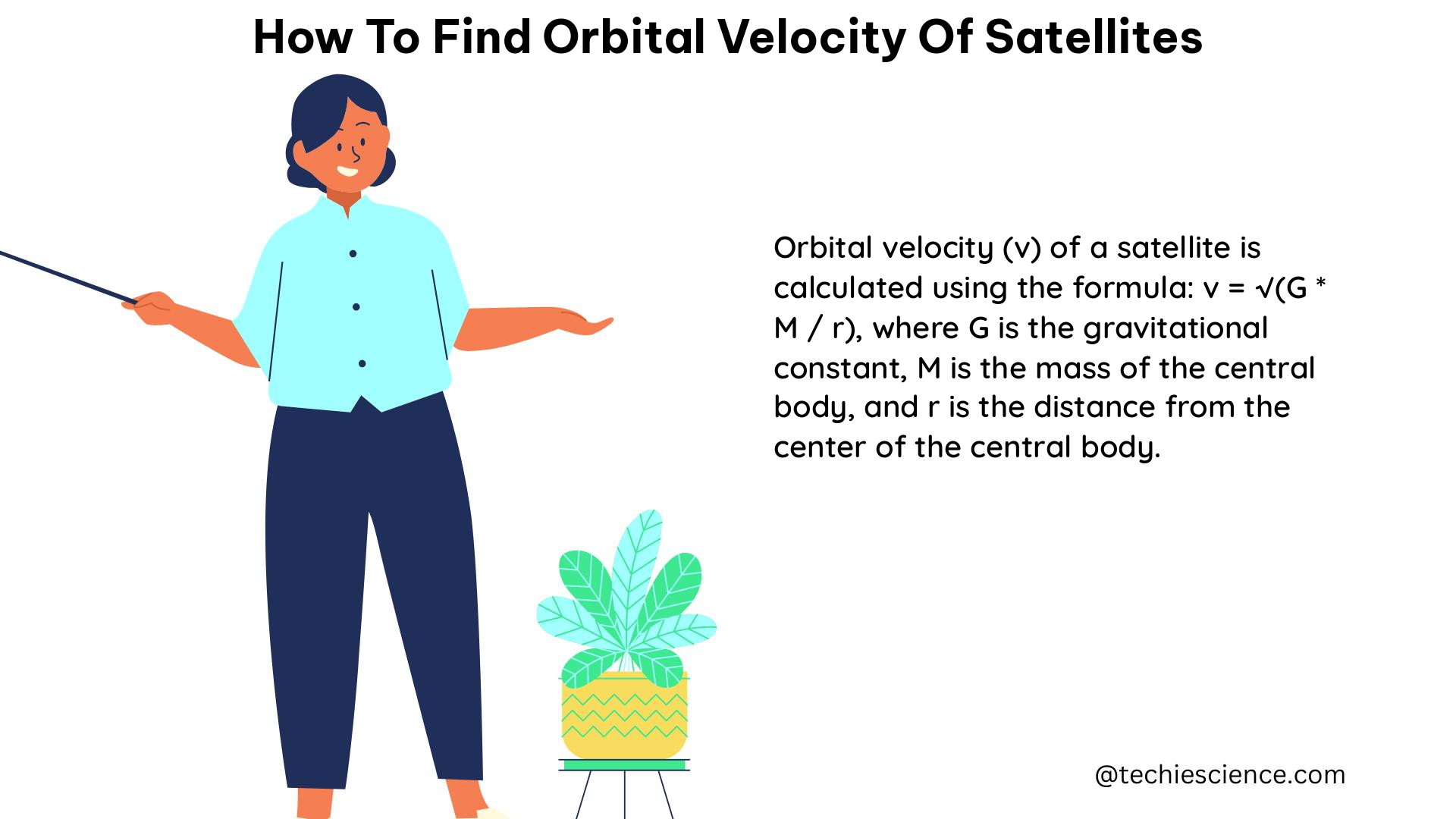
The formula used to calculate the orbital velocity of a satellite is:

Vorbital = √(GM / R)

Where:
– Vorbital is the orbital velocity of the satellite (in m/s)
– G is the gravitational constant (6.67408 × 10^-11 m^3 kg^-1 s^-2)
– M is the mass of the body at the center of the orbit (e.g., the mass of the Earth or Jupiter, in kg)
– R is the radius of the orbit (in m)

This formula is derived from the principles of Newtonian mechanics and the concept of centripetal force, which is the force that keeps the satellite in a circular orbit.

Calculating Orbital Velocity for Earth-Orbiting Satellites

Let’s consider the example of calculating the orbital velocity of a satellite orbiting the Earth. We’ll use the following values:

• Radius of the Earth (R): 6.5 × 10^6 m
• Mass of the Earth (M): 5.9722 × 10^24 kg
• Gravitational constant (G): 6.67408 × 10^-11 m^3 kg^-1 s^-2

Plugging these values into the formula, we get:

Vorbital = √[(6.67408 × 10^-11 m^3 kg^-1 s^-2) × (5.9722 × 10^24 kg) / (6.5 × 10^6 m)]
Vorbital = 7.5 × 10^3 m/s or 7.5 km/s

Therefore, the orbital velocity of a satellite around the Earth is approximately 7.5 km/s.

Calculating Orbital Velocity for Jupiter-Orbiting Satellites

Now, let’s consider the case of a satellite orbiting Jupiter. We’ll use the following values:

• Radius of Jupiter (R): 70.5 × 10^6 m
• Mass of Jupiter (M): 1.5 × 10^27 kg
• Gravitational constant (G): 6.67408 × 10^-11 m^3 kg^-1 s^-2

Plugging these values into the formula, we get:

Vorbital = √[(6.67408 × 10^-11 m^3 kg^-1 s^-2) × (1.5 × 10^27 kg) / (70.5 × 10^6 m)]
Vorbital = 3.75 × 10^4 m/s or 37.5 km/s

Therefore, the orbital velocity of a satellite around Jupiter is approximately 37.5 km/s.

Factors Affecting Orbital Velocity

The orbital velocity of a satellite is influenced by several factors, including:

1. Gravitational Constant (G): The gravitational constant is a fundamental physical constant that represents the strength of the gravitational force between two objects. It remains constant regardless of the celestial bodies involved.

2. Mass of the Central Body (M): The mass of the central body, such as the Earth or Jupiter, plays a crucial role in determining the orbital velocity. The greater the mass of the central body, the higher the orbital velocity required to maintain a stable orbit.

3. Radius of the Orbit (R): The distance between the satellite and the central body, or the radius of the orbit, is inversely proportional to the orbital velocity. As the radius increases, the orbital velocity decreases, and vice versa.

4. Orbital Altitude: The altitude of the satellite’s orbit also affects its orbital velocity. Satellites in lower orbits, such as Low Earth Orbit (LEO), typically have higher orbital velocities compared to satellites in higher orbits, such as Geostationary Orbit (GEO).

Practical Applications of Orbital Velocity

The understanding of orbital velocity is essential in various fields of space exploration and satellite technology, including:

1. Satellite Positioning and Tracking: Knowing the orbital velocity of a satellite is crucial for accurately predicting its position and trajectory, which is essential for satellite tracking and communication.

2. Satellite Launch and Deployment: The orbital velocity of a satellite must be precisely calculated to ensure a successful launch and deployment into the desired orbit.

3. Satellite Maneuvers and Orbit Maintenance: Adjusting the orbital velocity is necessary for performing satellite maneuvers, such as changing the orbit or maintaining a stable position.

4. Satellite Communication and Navigation: Satellites in different orbits, such as GPS satellites, rely on their orbital velocity to provide accurate communication and navigation services.

5. Interplanetary Missions: The calculation of orbital velocity is crucial for planning and executing interplanetary missions, where spacecraft need to achieve the necessary velocity to escape the gravitational pull of one planet and enter the orbit of another.

Conclusion

In this comprehensive guide, we have explored the fundamental principles and practical applications of calculating the orbital velocity of satellites. By understanding the orbital velocity formula and the factors that influence it, you can now confidently determine the orbital velocity of satellites around different celestial bodies, such as the Earth and Jupiter. This knowledge is essential for various fields of space exploration and satellite technology, from satellite positioning and tracking to interplanetary missions.

References

1. Orbital Velocity Formula – Solved Example with Equations – BYJU’S (https://byjus.com/orbital-velocity-formula/)
2. Orbital Velocity Formula – GeeksforGeeks (https://www.geeksforgeeks.org/orbital-velocity-formula/)
3. Speed of a Satellite in Circular Orbit, Orbital Velocity, Period … – YouTube (https://www.youtube.com/watch?v=QIaAleG0Eb4)
4. Orbital Mechanics – NASA (https://www.grc.nasa.gov/www/k-12/airplane/orbmech.html)
5. Orbital Velocity – HyperPhysics (http://hyperphysics.phy-astr.gsu.edu/hbase/mechanics/orbvel.html)