How To Find Normal Force Between Two Blocks: Several Approaches and Problem Examples

How to Find Normal Force Between Two Blocks

When it comes to understanding the interaction between two blocks, the concept of normal force plays a crucial role. The normal force is the force exerted by a surface to support the weight of an object resting on it. In the case of two blocks in contact, the normal force is the force exerted by one block on the other perpendicular to the contact surface. In this blog post, we will explore how to find the normal force between two blocks, considering various factors such as friction, gravity, mass, and weight.

Identifying the Variables

Before diving into the calculations, let’s familiarize ourselves with the variables involved in finding the normal force between two blocks.

m1 and m2: The masses of the two blocks, respectively.
g: The acceleration due to gravity (approximately 9.8 m/s^2).
N: The normal force between the two blocks.
F_applied: Any externally applied force on the system.
F_friction: The force of friction between the blocks, if present.

Applying the Formula for Finding Normal Force

To calculate the normal force between two blocks, we need to consider the forces acting on the system. Newton’s second law of motion states that the sum of all forces acting on an object is equal to the mass of the object multiplied by its acceleration. In this case, we can apply Newton’s second law to the system of two blocks.

The formula for finding the normal force can be derived from Newton’s second law as follows:

$Sigma F = m_{text{total}} cdot a$

Here, $Sigma F$ represents the sum of all forces acting on the system, $m_{text{total}}$ is the total mass of the system $sum of the masses of the two blocks), and (a$ is the acceleration of the system.

Since we want to find the normal force between the two blocks, we can rearrange the equation to solve for $N$ :

$N = m_{text{total}} cdot a - F_{text{applied}} - F_{text{friction}}$

Worked Out Example: Calculating Normal Force

Let’s consider an example to illustrate how to calculate the normal force between two blocks. Suppose we have two blocks with masses of 2 kg and 3 kg, respectively, resting on a frictionless surface. An external force of 20 N is applied to the system.

To find the normal force, we can follow these steps:

Calculate the total mass of the system: $m_{text{total}} = m_1 + m_2 = 2 , text{kg} + 3 , text{kg} = 5 , text{kg}$ .
Determine the acceleration of the system: Since there is no friction or any other external force acting on the blocks horizontally, the acceleration is zero $(a = 0$ ).
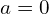Substitute the values into the formula to calculate the normal force: $N = 5 , text{kg} cdot 0 - 20 , text{N} - 0 = -20 , text{N}$ .

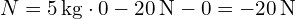In this example, the negative value of the normal force indicates that the blocks are being pushed against each other, rather than being pulled apart.

Factors Affecting the Normal Force Between Two Blocks

Now that we know how to calculate the normal force, let’s explore the factors that can affect its magnitude.

The Role of Friction in Determining Normal Force

When there is friction between the two blocks, the force of friction affects the normal force. The force of friction opposes the relative motion between the blocks and depends on the coefficient of friction $(mu$ ) and the normal force itself. The formula for calculating the force of friction is:

$F_{text{friction}} = mu cdot N$

Where $mu$ is the coefficient of friction.

The Impact of Gravity on Normal Force

The gravitational force acting on each block contributes to the normal force between them. The weight of each block creates a downward force due to gravity. The formula for calculating weight is:

$text{Weight} = m cdot g$

Where $m$ is the mass of the block and $g$ is the acceleration due to gravity.

The Effect of Mass and Weight on Normal Force

The mass and weight of the blocks also affect the normal force between them. As the mass or weight of the blocks increases, the normal force also increases. This is because the weight of the blocks creates a downward force that must be balanced by the normal force.

Advanced Concepts Related to Normal Force

Let’s explore a few advanced concepts related to the normal force between two blocks.

Understanding the Normal Reaction Between Two Blocks

The normal force can also be referred to as the normal reaction. It is called a reaction because it is a force that acts in response to another force (in this case, the weight of the blocks). The normal force is always perpendicular to the contact surface between the blocks.

How to Calculate the Tension Between Two Blocks

In situations where the two blocks are connected by a rope or a string, it is possible to calculate the tension between them. The tension is the force transmitted through the rope or string and is equal in magnitude to the normal force between the blocks. By calculating the normal force, we can determine the tension in the rope or string.

Worked Out Example: Finding Contact Force Between Two Blocks Without Friction

Suppose we have two blocks with masses of 4 kg and 6 kg, respectively, resting on a frictionless surface. An external force of 30 N is applied to the system.

To find the contact force between the two blocks (which is equivalent to the normal force), we can follow these steps:

Calculate the total mass of the system: $m_{text{total}} = m_1 + m_2 = 4 , text{kg} + 6 , text{kg} = 10 , text{kg}$ .
Determine the acceleration of the system: Since there is no friction or any other external force acting on the blocks horizontally, the acceleration is zero $(a = 0$ ).
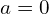Substitute the values into the formula to calculate the normal force: $N = 10 , text{kg} cdot 0 - 30 , text{N} - 0 = -30 , text{N}$ .

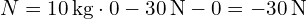In this example, the negative value of the normal force indicates that the blocks are being pushed against each other.

By understanding the concepts and formulas related to normal force, we can analyze and predict the behavior of blocks in various scenarios. Whether it’s calculating the normal force in a simple system or considering the impact of friction and gravity, mastering this concept is essential for understanding the physics of objects in motion.

Now that you have a solid understanding of how to find the normal force between two blocks, you can apply these concepts to a wide range of scenarios. Remember to consider factors such as friction, gravity, mass, and weight when calculating the normal force.

How does the concept of finding the normal force between two blocks relate to the idea of “Finding coefficient of kinetic friction”?

To understand how the concept of finding the normal force between two blocks intersects with the idea of “Finding coefficient of kinetic friction,” it is essential to consider the relationship between these two factors in a physics problem. The normal force is the perpendicular force exerted by a surface to support an object in contact, while the coefficient of kinetic friction represents the frictional force between two surfaces in relative motion. By determining the normal force, one can then calculate the coefficient of kinetic friction, as shown in the article “Finding coefficient of kinetic friction”. This article provides a comprehensive guide on how to calculate the coefficient of kinetic friction using various methods, which can be beneficial in scenarios where the normal force between two blocks is involved.

Numerical Problems on How to Find Normal Force Between Two Blocks

Problem 1:

Two blocks, A and B, are placed on top of each other on a horizontal surface. Block A has a mass of 5 kg and block B has a mass of 8 kg. The coefficient of friction between block A and the surface is 0.3, while the coefficient of friction between block B and block A is 0.2. Determine the normal force between the two blocks.

Solution:

Given:
– Mass of block A, $m_A = 5$ kg
– Mass of block B, $m_B = 8$ kg
– Coefficient of friction between block A and the surface, $mu_{A} = 0.3$
– Coefficient of friction between block B and block A, $mu_{B} = 0.2$

To find the normal force between the blocks, we need to consider the forces acting on each block individually.

For block A:
The weight of block A, $W_A = m_A cdot g$ , where $g$ is the acceleration due to gravity.
The normal force on block A, $N_A$ , is equal and opposite to the weight, so $N_A = W_A$ .
The friction force acting on block A, $F_{fA}$ , can be determined using the equation $F_{fA} = mu_{A} cdot N_A$ .

For block B:
The weight of block B, $W_B = m_B cdot g$ .
The friction force acting on block B, $F_{fB}$ , can be determined using the equation $F_{fB} = mu_{B} cdot N_A$ .

Since the two blocks are in contact with each other, the normal force acting on block B is equal to the friction force acting on block A, i.e., $N_B = F_{fA}$ .

Now, let’s calculate the normal force $N_A$ on block A:
$N_A = W_A = m_A cdot g$

Substituting the given values:
$N_A = 5 , text{kg} times 9.8 , text{m/s}^2$

Finally, we can calculate the normal force $N_B$ on block B:
$N_B = F_{fA} = mu_{A} cdot N_A$

Substituting the given values:
$N_B = 0.3 times N_A$

Calculating $N_B$ :
$N_B = 0.3 times (5 , text{kg} times 9.8 , text{m/s}^2)$

Hence, the normal force between the two blocks is $N_B$ .

Problem 2:

Two wooden blocks, P and Q, are placed on a table. Block P has a mass of 10 kg and block Q has a mass of 5 kg. The coefficient of friction between block P and the table is 0.4, while the coefficient of friction between block Q and the table is 0.3. Determine the normal force between the two blocks.

Solution:

Given:
– Mass of block P, $m_P = 10$ kg
– Mass of block Q, $m_Q = 5$ kg
– Coefficient of friction between block P and the table, $mu_{P} = 0.4$
– Coefficient of friction between block Q and the table, $mu_{Q} = 0.3$

To find the normal force between the blocks, we need to consider the forces acting on each block individually.

For block P:
The weight of block P, $W_P = m_P cdot g$ , where $g$ is the acceleration due to gravity.
The normal force on block P, $N_P$ , is equal and opposite to the weight, so $N_P = W_P$ .
The friction force acting on block P, $F_{fP}$ , can be determined using the equation $F_{fP} = mu_{P} cdot N_P$ .

For block Q:
The weight of block Q, $W_Q = m_Q cdot g$ .
The friction force acting on block Q, $F_{fQ}$ , can be determined using the equation $F_{fQ} = mu_{Q} cdot N_Q$ .

Since the two blocks are in contact with each other, the normal force acting on block Q is equal to the friction force acting on block P, i.e., $N_Q = F_{fP}$ .

Now, let’s calculate the normal force $N_P$ on block P:
$N_P = W_P = m_P cdot g$

Substituting the given values:
$N_P = 10 , text{kg} times 9.8 , text{m/s}^2$

Finally, we can calculate the normal force $N_Q$ on block Q:
$N_Q = F_{fP} = mu_{P} cdot N_P$

Substituting the given values:
$N_Q = 0.4 times N_P$

Calculating $N_Q$ :
$N_Q = 0.4 times (10 , text{kg} times 9.8 , text{m/s}^2)$

Hence, the normal force between the two blocks is $N_Q$ .

Problem 3:

Two blocks, X and Y, are connected by a string passing over a frictionless pulley. Block X has a mass of 6 kg and is on a horizontal surface, while block Y has a mass of 4 kg and is hanging vertically. Determine the normal force between the two blocks.

Solution:

Given:
– Mass of block X, $m_X = 6$ kg
– Mass of block Y, $m_Y = 4$ kg

To find the normal force between the blocks, we need to consider the forces acting on each block individually.

For block X:
The weight of block X, $W_X = m_X cdot g$ , where $g$ is the acceleration due to gravity.
The normal force on block X, $N_X$ , is equal and opposite to the weight, so $N_X = W_X$ .

For block Y:
The weight of block Y, $W_Y = m_Y cdot g$ .
The tension in the string, $T$ , is equal and opposite to the weight, so $T = W_Y$ .

Since the two blocks are connected, the normal force acting on block Y is equal to the tension in the string, i.e., $N_Y = T$ .

Now, let’s calculate the normal force $N_X$ on block X:
$N_X = W_X = m_X cdot g$

Substituting the given values:
$N_X = 6 , text{kg} times 9.8 , text{m/s}^2$

Finally, we can calculate the normal force $N_Y$ on block Y:
$N_Y = T = W_Y = m_Y cdot g$

Substituting the given values:
$N_Y = 4 , text{kg} times 9.8 , text{m/s}^2$

Hence, the normal force between the two blocks is $N_Y$ .

Also Read:

Riya Pandey

I am Riya Pandey. I have completed Post Graduation in physics in 2021. Currently I am working as a Subject Matter Expert in Physics for Lambdageeks. I try to explain Physics subject easily understandable in simple way.