How to Find Momentum from Mass and Velocity: A Comprehensive Guide

Momentum is a fundamental concept in physics that describes the quantity of motion possessed by an object. It is a vector quantity, meaning it has both magnitude and direction. The formula to calculate momentum from mass and velocity is a crucial tool for understanding and analyzing the behavior of objects in motion. In this comprehensive guide, we will delve into the details of this formula, provide practical examples, and explore the various applications of momentum in the world of physics.

Understanding the Momentum Formula

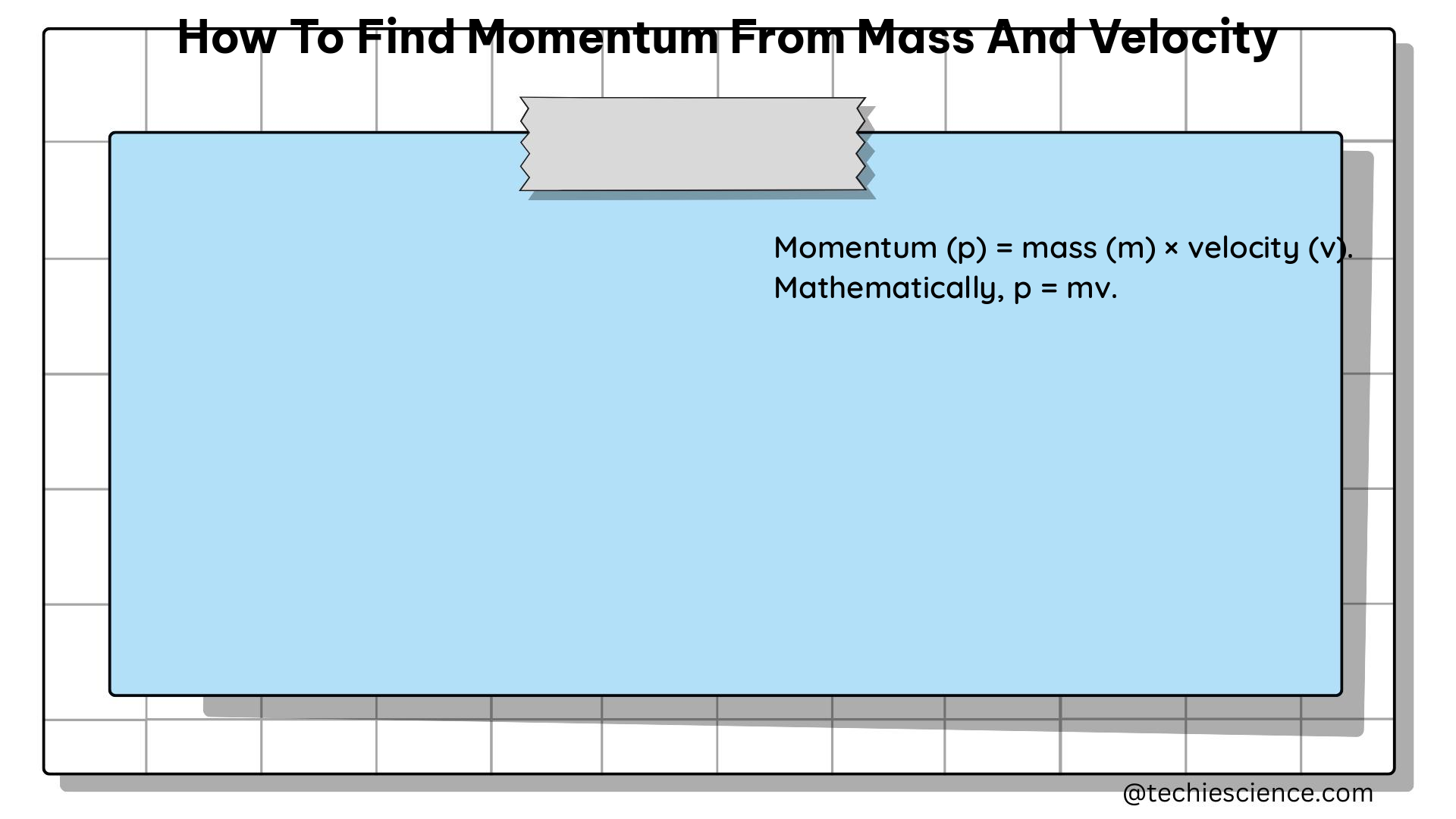
The formula to find momentum from mass and velocity is:

[p = m \times v]

where:
– p is the momentum (measured in kg · m/s)
– m is the mass of the object (measured in kg)
– v is the velocity of the object (measured in m/s)

This formula tells us that the momentum of an object is directly proportional to its mass and velocity. The greater the mass and velocity of an object, the greater its momentum.

Calculating Momentum from Mass and Velocity

Let’s explore some examples to understand how to apply the momentum formula in practice.

Example 1: Calculating Momentum of a Moving Object

Suppose you have an object with a mass of 5 kg moving at a velocity of 10 m/s. To find the momentum of this object, you would simply plug the values into the formula:

[p = m \times v = 5 \text{ kg} \times 10 \text{ m/s} = 50 \text{ kg} \cdot \text{m/s}]

Therefore, the momentum of the object is 50 kg · m/s.

Example 2: Calculating Mass from Momentum and Velocity

Now, let’s say you know the momentum and velocity of an object, and you need to find its mass. You can rearrange the momentum formula to solve for mass:

[m = \frac{p}{v}]

For instance, if the momentum is 30 kg · m/s and the velocity is 6 m/s, you can calculate the mass as follows:

[m = \frac{p}{v} = \frac{30 \text{ kg} \cdot \text{m/s}}{6 \text{ m/s}} = 5 \text{ kg}]

So, the mass of the object is 5 kg.

Example 3: Calculating Velocity from Momentum and Mass

Similarly, if you know the momentum and mass of an object, you can calculate its velocity. Rearranging the momentum formula, we get:

[v = \frac{p}{m}]

For example, if the momentum is 40 kg · m/s and the mass is 8 kg, you can find the velocity:

[v = \frac{p}{m} = \frac{40 \text{ kg} \cdot \text{m/s}}{8 \text{ kg}} = 5 \text{ m/s}]

Therefore, the velocity of the object is 5 m/s.

Momentum and Conservation of Momentum

Momentum is a conserved quantity, meaning that the total momentum of a closed system remains constant unless an external force acts on the system. This principle, known as the conservation of momentum, is a fundamental law in physics and has numerous applications in various fields, such as:

1. Collisions: When two objects collide, the total momentum of the system is conserved, and the momentum before the collision is equal to the momentum after the collision (assuming no external forces).
2. Rocket Propulsion: The principle of conservation of momentum is the basis for rocket propulsion, where the momentum of the exhaust gases is transferred to the rocket, causing it to move in the opposite direction.
3. Particle Physics: In particle physics, the conservation of momentum is used to study the behavior of subatomic particles and to understand the fundamental interactions in the universe.

Advanced Concepts and Applications

Momentum is a versatile concept in physics, and its applications extend beyond the basic formula and examples presented here. Some advanced topics and applications include:

1. Relativistic Momentum: In the realm of special relativity, the formula for momentum needs to be modified to account for the effects of high-speed motion and the relationship between mass, energy, and velocity.
2. Angular Momentum: Momentum can also be applied to rotational motion, where the concept of angular momentum is used to describe the motion of objects around a fixed axis.
3. Momentum in Quantum Mechanics: In quantum mechanics, momentum is a fundamental property of particles and is used to describe the wave-like behavior of matter.
4. Momentum in Fluid Dynamics: Momentum is a crucial concept in fluid dynamics, where it is used to analyze the behavior of fluids, such as the lift generated by wings and the drag experienced by objects moving through fluids.

Conclusion

Mastering the concept of momentum and the ability to calculate it from mass and velocity is a crucial skill for any physics student or enthusiast. By understanding the momentum formula, working through practical examples, and exploring the broader applications of momentum, you can develop a deeper understanding of the fundamental principles that govern the motion of objects in the physical world.

Reference:

1. Khan Academy – Introduction to Momentum
2. CK-12 – How can mass be calculated using momentum and velocity?
3. GeeksforGeeks – How to find the Momentum from Velocity?