Mastering the Art of Finding Mass Using Potential Energy and Velocity

In the realm of physics, understanding the relationship between potential energy, velocity, and mass is crucial for a wide range of applications, from engineering to astrophysics. This comprehensive guide will delve into the intricacies of how to determine the mass of an object using its potential energy and velocity, equipping you with the necessary knowledge and tools to tackle this fundamental problem.

Understanding the Underlying Principles

The formula used to find the mass of an object using potential energy and velocity is derived from the principles of conservation of energy. When an object is raised to a certain height, it gains potential energy due to the work done against gravity. As the object falls, this potential energy is converted into kinetic energy, which is directly proportional to the object’s mass and the square of its velocity.

The relationship between these variables can be expressed as:

V = √(2 * PE / m)

Where:
– V is the velocity of the object (in m/s)
– PE is the potential energy of the object (in J)
– m is the mass of the object (in kg)

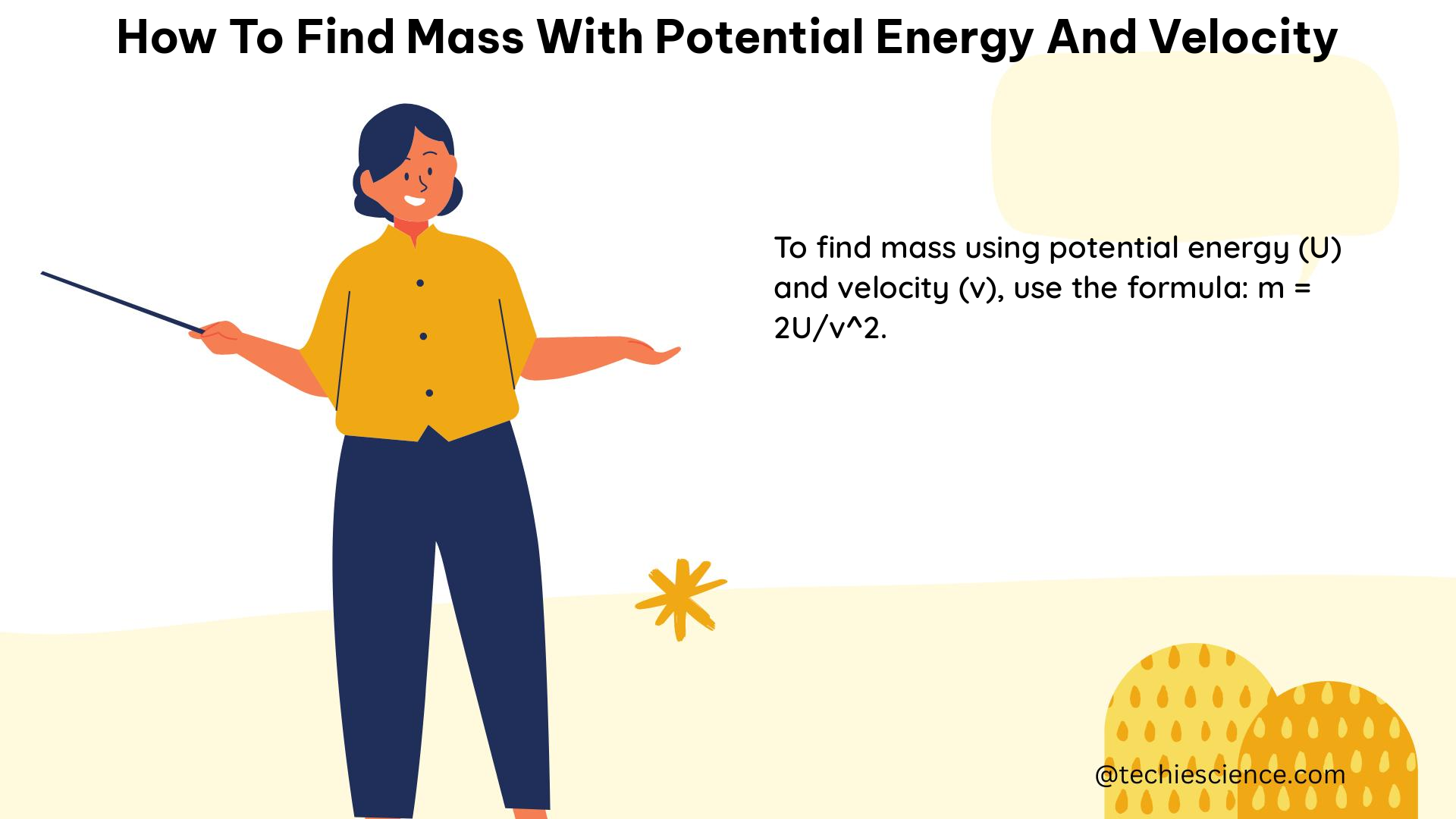
By rearranging this equation, we can solve for the mass:

m = 2 * PE / V^2

Measuring Potential Energy

To determine the mass of an object using this formula, you first need to measure its potential energy. Potential energy is the energy an object possesses due to its position or state, and it can be calculated using the following formula:

PE = m * g * h

Where:
– PE is the potential energy (in J)
– m is the mass of the object (in kg)
– g is the acceleration due to gravity (9.8 m/s²)
– h is the height to which the object is raised (in m)

To measure the potential energy, you can follow these steps:

1. Determine the mass of the object using a scale or balance.
2. Measure the height to which the object is raised.
3. Substitute the values of mass and height into the potential energy formula to calculate the potential energy.

Measuring Velocity

The next step is to measure the velocity of the object. This can be done using a variety of methods, depending on the specific situation and the equipment available. Some common techniques include:

1. Timing the object’s motion: Measure the distance the object travels and the time it takes to cover that distance, then calculate the velocity using the formula V = d / t.
2. Using a velocity sensor: Employ a device that can directly measure the object’s velocity, such as a radar gun or a Doppler radar.
3. Analyzing video footage: Record the object’s motion and use video analysis software to track its position over time, then calculate the velocity.

Ensure that the velocity measurement is accurate and consistent with the potential energy measurement to obtain reliable results.

Calculating the Mass

Once you have the values for potential energy and velocity, you can substitute them into the formula m = 2 * PE / V^2 to calculate the mass of the object.

For example, let’s say you have an object with a potential energy of 50 J and a velocity of 5 m/s. Plugging these values into the formula, we get:

m = 2 * 50 J / (5 m/s)^2
m = 2 * 50 J / 25 m^2/s^2
m = 4 kg

Therefore, the mass of the object is 4 kg.

Practical Applications and Considerations

The ability to determine the mass of an object using potential energy and velocity has numerous practical applications, including:

1. Mechanical engineering: Calculating the mass of components in machinery, vehicles, or structures to ensure proper design and performance.
2. Aerospace engineering: Determining the mass of spacecraft, satellites, or aircraft to optimize their design and trajectory.
3. Sports and biomechanics: Analyzing the motion and performance of athletes by measuring their potential energy and velocity.
4. Astrophysics: Estimating the mass of celestial bodies, such as planets or stars, based on their gravitational potential energy and observed velocities.

When applying this method, it’s important to consider the following factors:

• Accuracy of measurements: Ensure that the potential energy and velocity measurements are as precise as possible to minimize errors in the mass calculation.
• Environmental conditions: Take into account any external factors, such as air resistance or friction, that may affect the object’s motion and the validity of the assumptions.
• Limitations of the formula: The formula assumes that the object’s motion is not influenced by other forces, such as air resistance or friction. In real-world scenarios, these factors may need to be accounted for.

Conclusion

Mastering the art of finding mass using potential energy and velocity is a valuable skill in the field of physics. By understanding the underlying principles, learning the necessary measurement techniques, and applying the appropriate calculations, you can accurately determine the mass of an object in a wide range of applications. This knowledge not only enhances your understanding of fundamental physics concepts but also equips you with the tools to tackle complex problems in various scientific and engineering disciplines.

References

1. Kinetic Energy and Velocity Lab – Arbor Scientific. https://www.arborsci.com/blogs/cool/kinetic-energy-and-velocity
2. Relativistic Energy | Physics – Lumen Learning. https://courses.lumenlearning.com/suny-physics/chapter/28-6-relativistic-energy/
3. Motion of a Mass on a Spring – The Physics Classroom. https://www.physicsclassroom.com/class/waves/Lesson-0/Motion-of-a-Mass-on-a-Spring
4. Velocity from Potential Energy Calculator. https://calculator.academy/velocity-from-potential-energy-calculator/
5. Gravitational Potential Energy Part 2 – Calculating Mass – YouTube. https://www.youtube.com/watch?v=j6JE91JI-nM