How to Find the Kinetic Energy of an Electron: A Comprehensive Guide

Summary

Determining the kinetic energy of an electron is a crucial step in understanding the behavior and properties of this fundamental particle in various physical and technological applications. This comprehensive guide will walk you through the step-by-step process of calculating the kinetic energy of an electron, including the use of the relativistic kinetic energy formula, the Lorentz factor, and the necessary physical constants. Whether you’re a physics student or a researcher, this guide will provide you with the knowledge and tools to accurately determine the kinetic energy of an electron.

Understanding Relativistic Kinetic Energy

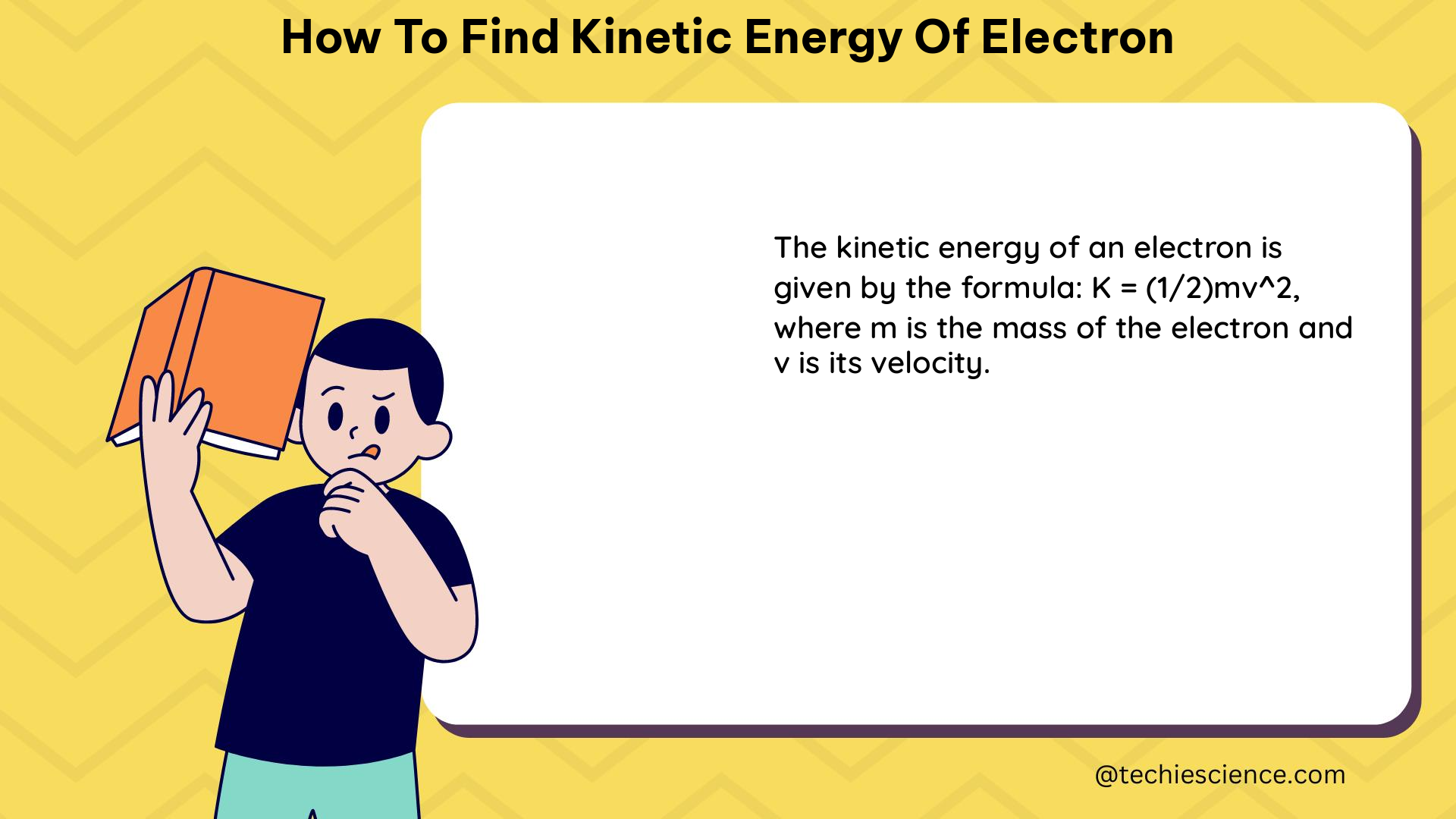
In the realm of classical mechanics, the kinetic energy of a particle is given by the formula:

KE = 1/2 * m * v^2

where m is the mass of the particle and v is its velocity. However, when dealing with particles moving at high velocities, such as electrons, the effects of special relativity must be taken into account. The relativistic kinetic energy formula is given by:

KE = (γ - 1) * m * c^2

where γ (gamma) is the Lorentz factor, m is the rest mass of the electron, and c is the speed of light.

The Lorentz factor is calculated as:

γ = 1 / √(1 - v^2/c^2)

where v is the velocity of the electron.

Calculating the Kinetic Energy of an Electron

To find the kinetic energy of an electron, you will need to follow these steps:

1. Determine the Velocity of the Electron: The first step is to know the velocity of the electron, either in absolute terms (e.g., 0.99c) or as a fraction of the speed of light.

2. Calculate the Lorentz Factor: Using the velocity of the electron, calculate the Lorentz factor γ using the formula:

γ = 1 / √(1 - v^2/c^2)

1. Determine the Rest Mass of the Electron: The rest mass of an electron is approximately 9.11 × 10^-31 kg.

2. Apply the Relativistic Kinetic Energy Formula: Plug the Lorentz factor γ, the rest mass of the electron m, and the speed of light c into the relativistic kinetic energy formula:

KE = (γ - 1) * m * c^2

This will give you the kinetic energy of the electron in Joules (J).

1. Convert to MeV (Optional): If you want to express the kinetic energy in mega-electron volts (MeV), you can use the conversion factor of 1 MeV = 1.602 × 10^-13 J:

KE (MeV) = KE (J) / (1.602 × 10^-13 J/MeV)

Example Calculation

Let’s say we have an electron moving at a velocity of 0.99c (99% the speed of light).

1. Velocity of the electron: v = 0.99c
2. Lorentz factor:
   γ = 1 / √(1 - (0.99c)^2/c^2) = 7.0888
3. Rest mass of the electron: m = 9.11 × 10^-31 kg
4. Relativistic kinetic energy:
   KE = (γ - 1) * m * c^2 = (7.0888 - 1) * 9.11 × 10^-31 kg * (2.998 × 10^8 m/s)^2 = 1.50 × 10^-10 J
5. Conversion to MeV:
   KE (MeV) = 1.50 × 10^-10 J / (1.602 × 10^-13 J/MeV) = 93.6 MeV

Therefore, the kinetic energy of the electron moving at 0.99c is approximately 93.6 MeV.

Factors Affecting Kinetic Energy of Electrons

The kinetic energy of an electron is primarily influenced by two factors:

1. Velocity: As the velocity of the electron increases, its kinetic energy increases exponentially due to the relativistic effects. This is captured by the Lorentz factor γ in the relativistic kinetic energy formula.

2. Rest Mass: The rest mass of the electron, which is approximately 9.11 × 10^-31 kg, also plays a crucial role in determining the kinetic energy. Heavier particles will have higher kinetic energies at the same velocity compared to lighter particles.

It’s important to note that the relativistic kinetic energy formula is valid for all particles, not just electrons, as long as the particle’s velocity is close to the speed of light.

Applications and Importance of Electron Kinetic Energy

Knowing the kinetic energy of electrons is essential in various fields of physics and technology, including:

1. Particle Accelerators: Particle accelerators, such as linear accelerators and cyclotrons, are used to accelerate charged particles, including electrons, to high velocities. Understanding the kinetic energy of these accelerated electrons is crucial for the design and operation of these devices.

2. Radiation and Medical Imaging: High-energy electrons can be used to generate X-rays or other forms of radiation, which are widely used in medical imaging techniques like CT scans and radiotherapy. Accurate knowledge of the electron kinetic energy is necessary for optimizing these applications.

3. Semiconductor Electronics: In semiconductor devices, such as transistors and integrated circuits, the kinetic energy of electrons plays a crucial role in the transport and behavior of charge carriers, which is fundamental to the operation of these electronic components.

4. Astrophysics and Plasma Physics: In astrophysical and plasma physics research, the kinetic energy of electrons is studied to understand the behavior of high-energy particles in various environments, such as in the solar corona or in fusion reactors.

5. Fundamental Research: The study of the kinetic energy of electrons is also essential for advancing our understanding of the fundamental properties of matter and the behavior of subatomic particles in various physical phenomena.

Conclusion

Determining the kinetic energy of an electron is a crucial step in understanding the behavior and properties of this fundamental particle in various physical and technological applications. By following the step-by-step process outlined in this guide, you can accurately calculate the kinetic energy of an electron using the relativistic kinetic energy formula, the Lorentz factor, and the necessary physical constants. This knowledge is essential for fields ranging from particle accelerators and medical imaging to semiconductor electronics and astrophysics research.

Reference:

1. Relativistic Energy – Douglas College Physics 1207: https://pressbooks.bccampus.ca/introductorygeneralphysics2phys1207opticsfirst/chapter/28-6-relativistic-energy/
2. Kinetic Molecular Theory of Gases – Introductory Chemistry: https://opentextbc.ca/introductorychemistry/chapter/kinetic-molecular-theory-of-gases/
3. Relativistic Energy | Physics – Lumen Learning: https://courses.lumenlearning.com/suny-physics/chapter/28-6-relativistic-energy/