How to Find Kinetic Energy from Momentum: A Comprehensive Guide

Summary

Kinetic energy (KE) and momentum (p) are two fundamental concepts in classical mechanics. This comprehensive guide will walk you through the step-by-step process of calculating kinetic energy from momentum, providing you with a deep understanding of the underlying physics principles, formulas, examples, and practical applications.

Understanding the Relationship between Kinetic Energy and Momentum

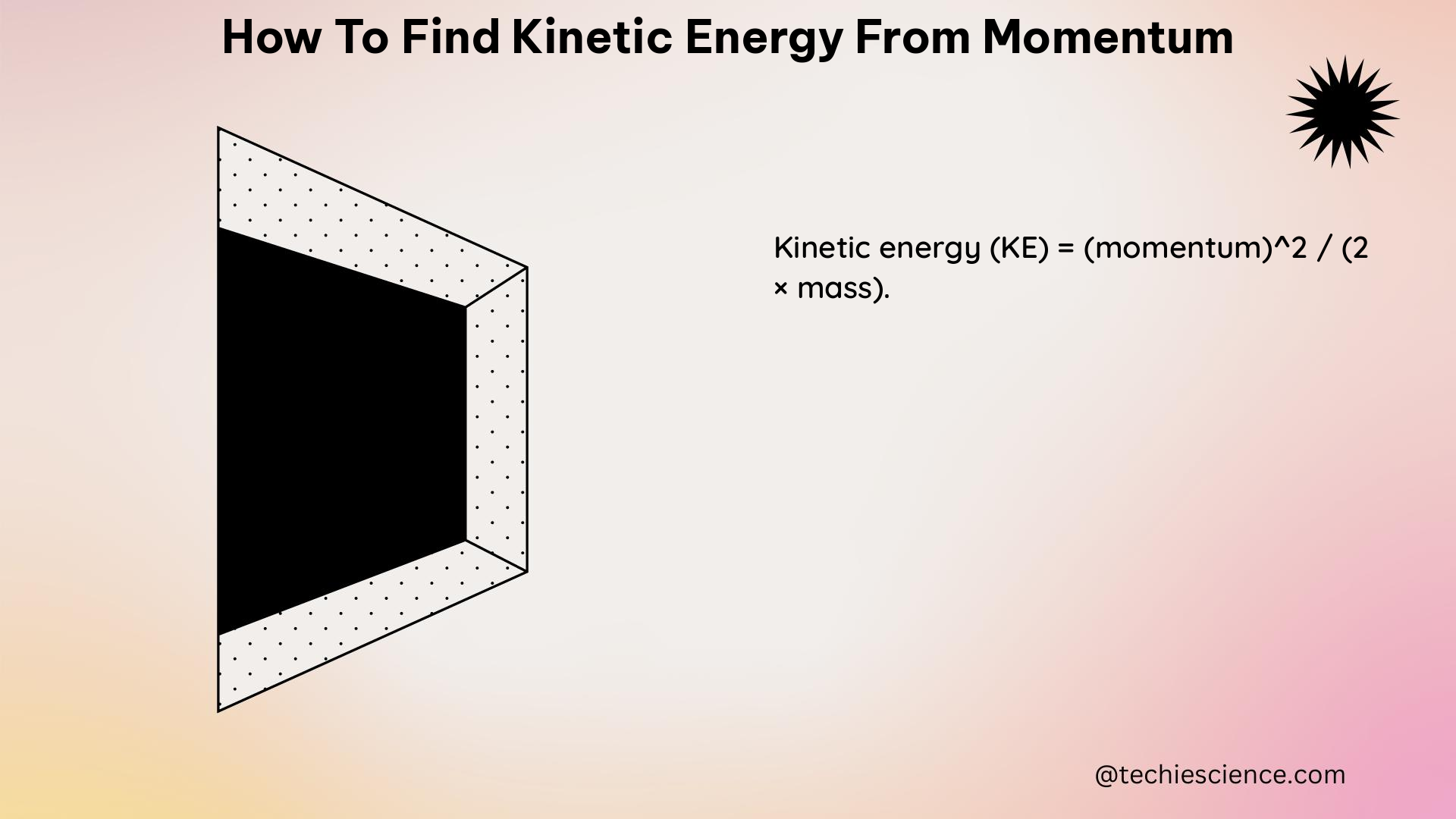
In classical mechanics, the kinetic energy (KE) of an object is defined as the work required to accelerate the object from rest to a given velocity. The formula for kinetic energy is:

KE = 1/2 * m * v^2

where:
– KE is the kinetic energy
– m is the mass of the object
– v is the velocity of the object

Momentum (p) is defined as the product of an object’s mass and velocity:

p = m * v

By substituting the momentum formula into the kinetic energy formula, we can derive the following equation:

KE = p^2 / (2 * m)

This formula allows us to calculate the kinetic energy of an object directly from its momentum and mass.

Measuring Mass and Momentum

To use the formula KE = p^2 / (2 * m), you need to have accurate measurements of the object’s mass (m) and momentum (p).

Measuring Mass

The mass of an object can be measured using a scale or balance. The most common types of scales used for this purpose are:
– Mechanical scales
– Digital scales
– Analytical balances

The accuracy and precision of the mass measurement will depend on the type of scale used and the specific application.

Measuring Momentum

Momentum (p) is the product of an object’s mass (m) and velocity (v):

p = m * v

To measure momentum, you need to measure both the mass and the velocity of the object. The mass can be measured using a scale, as mentioned earlier. The velocity can be measured using various devices, such as:
– Speedometers
– Radar guns
– Laser-based velocity sensors

The accuracy and precision of the momentum measurement will depend on the accuracy of the mass and velocity measurements.

Calculating Kinetic Energy from Momentum

Once you have the mass (m) and momentum (p) of the object, you can use the formula KE = p^2 / (2 * m) to calculate the kinetic energy.

Here’s an example calculation:

Suppose you have an object with a mass of 5 kg and a momentum of 20 kg * m/s. To calculate the kinetic energy, you would use the formula:

KE = p^2 / (2 * m)
KE = (20 kg * m/s)^2 / (2 * 5 kg)
KE = 400 J

Therefore, the kinetic energy of the object is 400 Joules.

Limitations and Considerations

It’s important to note that the formula KE = p^2 / (2 * m) is only valid for classical mechanics, where the velocities are much less than the speed of light. For objects moving at relativistic speeds (close to the speed of light), you would need to use the relativistic energy formula, which takes into account the effects of special relativity.

Additionally, the accuracy of the kinetic energy calculation will depend on the accuracy of the mass and momentum measurements. Careful attention should be paid to the units and the precision of the measurements to ensure reliable results.

Practical Applications

The ability to calculate kinetic energy from momentum has numerous practical applications in various fields, including:

1. Particle Physics: In high-energy particle accelerators, the kinetic energy of particles is a crucial parameter for understanding their behavior and interactions.
2. Aerospace Engineering: Calculating the kinetic energy of spacecraft and aircraft is essential for understanding their performance, energy requirements, and the forces acting on them during flight.
3. Automotive Engineering: Determining the kinetic energy of vehicles is important for understanding their braking distances, collision dynamics, and energy efficiency.
4. Sports Science: Analyzing the kinetic energy of athletes and sports equipment can provide insights into their performance, technique, and the forces involved in various sports activities.
5. Robotics and Automation: Calculating the kinetic energy of robotic systems is crucial for understanding their dynamics, control, and energy consumption.

Conclusion

In this comprehensive guide, we have explored the relationship between kinetic energy and momentum, and how to calculate kinetic energy from momentum using the formula KE = p^2 / (2 * m). We have also discussed the importance of accurate mass and momentum measurements, as well as the limitations and practical applications of this approach.

By understanding the principles and techniques presented in this guide, you will be better equipped to tackle problems involving kinetic energy and momentum in various fields of physics and engineering.

Reference:

1. Kinetic Energy, Momentum, and Newton’s Second Law
2. Relativistic Energy and Momentum
3. How to Calculate Kinetic Energy