The impulse-momentum theorem is a fundamental principle in physics that relates the impulse applied to an object to the change in its momentum. This theorem provides a powerful tool for analyzing the dynamics of various systems, from collisions to the motion of projectiles. In this comprehensive guide, we will delve into the details of how to find impulse from momentum, covering both the theoretical foundations and practical applications.
Understanding the Impulse-Momentum Theorem
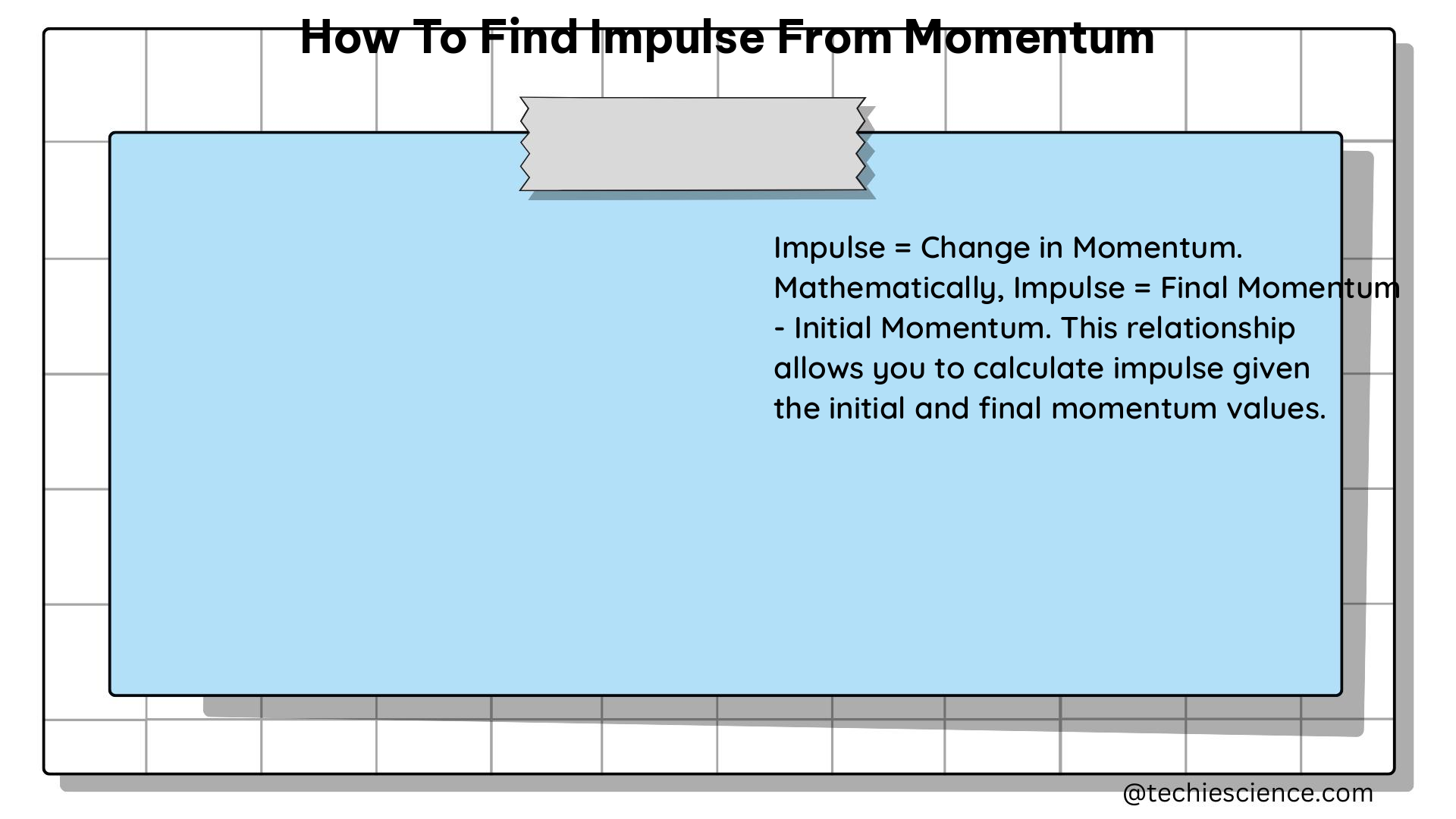
The impulse-momentum theorem states that the impulse applied to an object is equal to the change in the object’s momentum. Mathematically, this can be expressed as:
Impulse (J) = Momentum (p) final – Momentum (p) initial
or
J = pf – pi
where pf is the final momentum of the object and pi is the initial momentum.
To use this theorem, you need to know the initial and final momenta of the object. The initial momentum can be calculated by multiplying the initial velocity of the object by its mass:
pi = m * vi
where m is the mass of the object and vi is the initial velocity.
Similarly, the final momentum can be calculated by multiplying the final velocity of the object by its mass:
pf = m * vf
where vf is the final velocity.
Once you have calculated the initial and final momenta, you can find the impulse by subtracting the initial momentum from the final momentum:
J = pf - pi
Calculating Impulse from a Force-Time Graph
To find the impulse from a force-time graph, you can calculate the area under the curve of the graph. If the force is constant, the impulse can be calculated by multiplying the force by the time:
J = F * t
where F is the force and t is the time.
If the force is not constant, you can use calculus to find the area under the curve. This can be done by dividing the area under the curve into rectangles and triangles and calculating the area of each shape.
For example, suppose a force of 10 N is applied to an object for 2 seconds. The impulse can be calculated as:
J = F * t
J = 10 N * 2 s
J = 20 Ns
If the force is not constant, you can use calculus to find the area under the curve. For instance, if the force decreases linearly from 10 N to 5 N over 2 seconds, the impulse can be calculated as:
J = ∫F(t) dt
J = ∫(10 N - 5 N/s * t) dt from 0 to 2 s
J = [10 N * t - 2.5 N/s * t^2] from 0 to 2 s
J = (20 Ns - 10 Ns)
J = 10 Ns
In this case, the impulse is half of what it would be if the force were constant.
Calculating Impulse from a Velocity-Time Graph
To find the impulse from a velocity-time graph, you can calculate the area between the curve and the x-axis. If the velocity is constant, the impulse can be calculated by multiplying the velocity by the time:
J = m * Δv
where m is the mass of the object and Δv is the change in velocity.
If the velocity is not constant, you can use calculus to find the area between the curve and the x-axis. This can be done by dividing the area between the curve and the x-axis into rectangles and triangles and calculating the area of each shape.
For example, suppose an object with a mass of 5 kg has a velocity of 10 m/s at time t = 0 and a velocity of 20 m/s at time t = 2 s. The impulse can be calculated as:
J = m * Δv
J = 5 kg * (20 m/s - 10 m/s)
J = 5 kg * 10 m/s
J = 50 kg m/s
If the velocity increases linearly from 10 m/s to 20 m/s over 2 seconds, the impulse can be calculated as:
J = m * ∫(10 m/s + 5 m/s/s * t) dt from 0 to 2 s
J = 5 kg * [10 m/s * t + 2.5 m/s/s * t^2] from 0 to 2 s
J = 5 kg * (20 m/s + 10 m/s)
J = 5 kg * 30 m/s
J = 150 kg m/s
In this case, the impulse is three times what it would be if the velocity were constant.
Calculating Impulse from a Force-Position Graph
To find the impulse from a force-position graph, you can calculate the area under the curve of the graph. If the force is constant, the impulse can be calculated by multiplying the force by the time:
J = F * t
where F is the force and t is the time.
If the force is not constant, you can use calculus to find the area under the curve. This can be done by dividing the area under the curve into rectangles and triangles and calculating the area of each shape.
For example, suppose a force of 10 N is applied to an object that moves a distance of 2 m. The impulse can be calculated as:
J = F * t
J = 10 N * 2 m / 10 m/s
J = 2 Ns
If the force decreases linearly from 10 N to 5 N over 2 m, the impulse can be calculated as:
J = ∫F(x) dx
J = ∫(10 N - 5 N/m * x) dx from 0 to 2 m
J = [10 N * x - 2.5 N/m * x^2] from 0 to 2 m
J = (20 Nm - 10 Nm)
J = 10 Nm
In this case, the impulse is half of what it would be if the force were constant.
Calculating Impulse from a Velocity-Position Graph
To find the impulse from a velocity-position graph, you can calculate the area between the curve and the x-axis. If the velocity is constant, the impulse can be calculated by multiplying the velocity by the time:
J = m * Δv
where m is the mass of the object and Δv is the change in velocity.
If the velocity is not constant, you can use calculus to find the area between the curve and the x-axis. This can be done by dividing the area between the curve and the x-axis into rectangles and triangles and calculating the area of each shape.
For example, suppose an object with a mass of 5 kg has a velocity of 10 m/s at position x = 0 and a velocity of 20 m/s at position x = 2 m. The impulse can be calculated as:
J = m * Δv
J = 5 kg * (20 m/s - 10 m/s)
J = 5 kg * 10 m/s
J = 50 kg m/s
If the velocity increases linearly from 10 m/s to 20 m/s over 2 m, the impulse can be calculated as:
J = m * ∫(10 m/s + 5 m/s/m * x) dx from 0 to 2 m
J = 5 kg * [10 m/s * x + 2.5 m/s/m * x^2] from 0 to 2 m
J = 5 kg * (20 m/s + 10 m/s)
J = 5 kg * 30 m/s
J = 150 kg m/s
In this case, the impulse is three times what it would be if the velocity were constant.
Conclusion
In summary, to find impulse from momentum, you can use the impulse-momentum theorem, which states that the impulse applied to an object is equal to the change in the object’s momentum. You can calculate the initial and final momenta of the object by multiplying the mass of the object by its initial and final velocities, and then find the impulse by subtracting the initial momentum from the final momentum.
If the force or velocity is not constant, you can use calculus to find the area under the curve of the force-time graph, velocity-time graph, force-position graph, or velocity-position graph. This involves dividing the area into rectangles and triangles and calculating the area of each shape.
By understanding the principles and techniques presented in this guide, you will be well-equipped to tackle a wide range of problems involving the calculation of impulse from momentum, whether in the context of collisions, projectile motion, or other dynamic systems.
References
- How to Calculate Impulse Using a Force vs. Time Graph – YouTube
- Impulse-Momentum: Are You Accurately Measuring Jump Height?
- Impulse and Momentum – e-learning @ UF
- How to Calculate Impulse and Momentum – Study.com

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.