Summary
Horizontal acceleration is a crucial concept in physics, describing the rate of change in an object’s horizontal velocity. This comprehensive guide will delve into the various methods and formulas used to calculate horizontal acceleration, providing a detailed, step-by-step approach for physics students and enthusiasts. From the fundamental equation of Ax = A * Cos(a) to more complex scenarios involving friction, this article will equip you with the knowledge and tools necessary to tackle a wide range of horizontal acceleration problems.
Understanding the Fundamental Equation
The most basic equation for finding horizontal acceleration is:
Ax = A * Cos(a)
Where:
– Ax is the horizontal acceleration (in m/s²)
– A is the magnitude of the acceleration (in m/s²)
– a is the angle of acceleration (in degrees)
To use this equation, you need to know the magnitude of the acceleration and the angle at which the acceleration is acting. By multiplying the magnitude of the acceleration by the cosine of the angle, you can determine the horizontal component of the acceleration.
For example, if the magnitude of the acceleration is 130 m/s² and the angle of acceleration is 60 degrees, the horizontal acceleration would be:
Ax = 130 * Cos(60°) = 65 m/s²
This equation is particularly useful in scenarios where an object is moving at an angle, such as a projectile motion or a car turning a corner.
Calculating Horizontal Acceleration from Velocity Changes
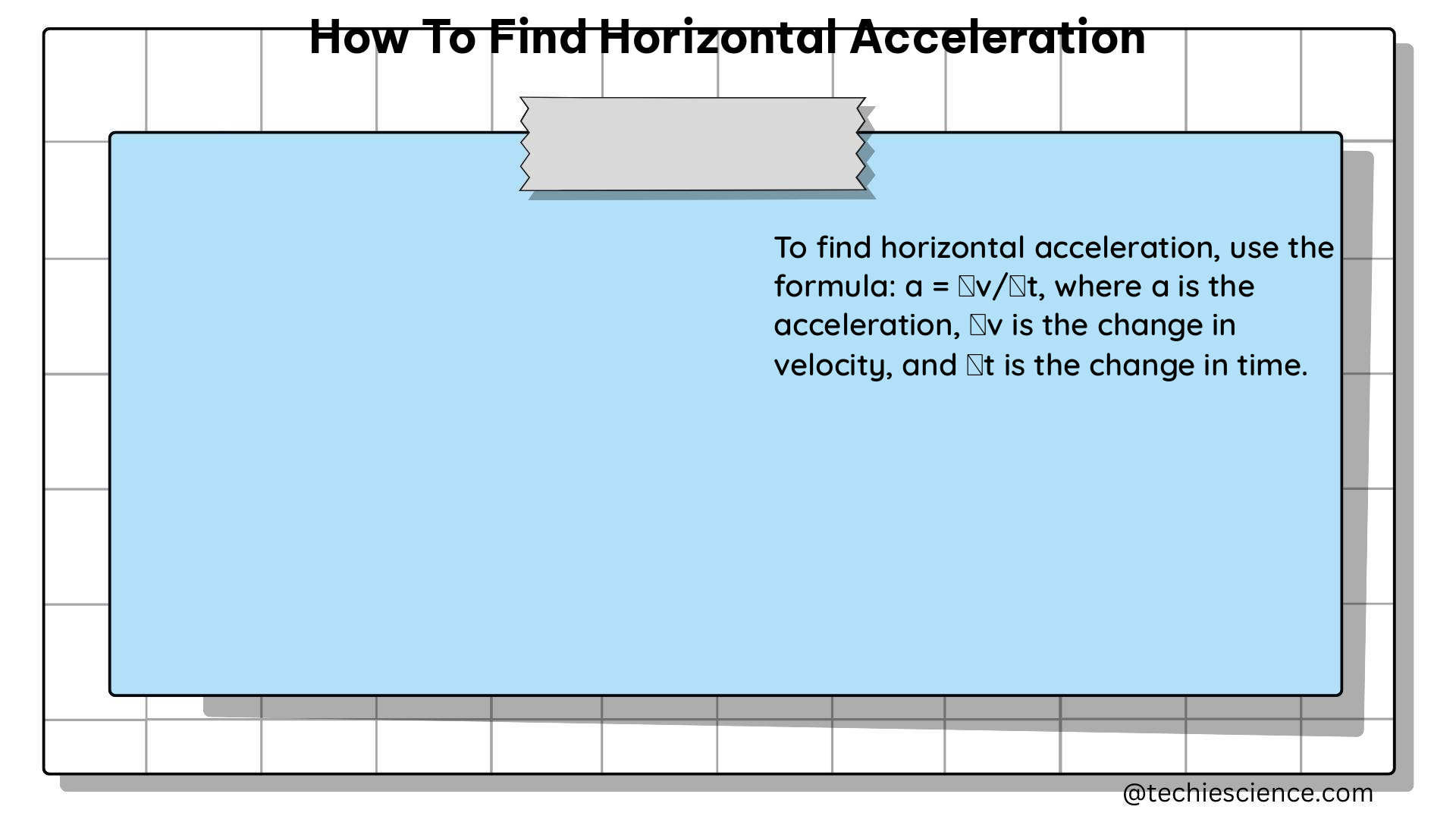
Another way to find horizontal acceleration is by using the formula:
a = Δv/Δt
Where:
– a is the acceleration (in m/s²)
– Δv is the change in velocity (in m/s)
– Δt is the change in time (in s)
This formula is based on the definition of acceleration as the rate of change in velocity. By dividing the change in an object’s horizontal velocity by the change in time, you can determine the horizontal acceleration.
For example, if an object’s horizontal velocity changes from 10 m/s to 20 m/s over a period of 5 seconds, the horizontal acceleration would be:
a = (20 m/s – 10 m/s) / 5 s = 2 m/s²
This method is useful when you have information about the object’s initial and final horizontal velocities, as well as the time interval over which the change occurred.
Horizontal Acceleration in Systems with Friction
When dealing with systems that involve friction, the calculation of horizontal acceleration becomes more complex. In these cases, you need to consider the forces acting on the object, including the force of kinetic friction.
The force of kinetic friction can be calculated using the equation:
Fk = μk * N
Where:
– Fk is the force of kinetic friction (in N)
– μk is the coefficient of kinetic friction (dimensionless)
– N is the normal force (in N)
In the case of a horizontal surface, the normal force is equal to the object’s weight, which can be calculated as N = m * g, where m is the mass of the object and g is the acceleration due to gravity (9.81 m/s²).
Once you have the force of kinetic friction, you can use the equation:
F – Fk = m * a
Where:
– F is the net force acting on the object (in N)
– m is the mass of the object (in kg)
– a is the acceleration (in m/s²)
Rearranging this equation, you can solve for the horizontal acceleration:
a = (F – Fk) / m
For example, if a hockey puck with a mass of 2 kg is subjected to a force of 30 N, and the coefficient of kinetic friction with the ice is 0.07, the horizontal acceleration would be:
Fk = (0.07)(2 kg)(9.81 m/s²) = 1.37 N
F – Fk = 30 N – 1.37 N = 28.63 N
a = (28.63 N) / (2 kg) = 14.32 m/s²
This approach is essential when analyzing the motion of objects on surfaces with friction, such as a car on a road or a block sliding on a table.
Advanced Techniques and Considerations
Inclined Planes
When an object is moving on an inclined plane, the horizontal acceleration can be calculated using the following equation:
Ax = a * Cos(θ)
Where:
– Ax is the horizontal acceleration (in m/s²)
– a is the total acceleration (in m/s²)
– θ is the angle of the inclined plane (in degrees)
This equation is similar to the fundamental equation, but it takes into account the angle of the inclined plane. By multiplying the total acceleration by the cosine of the angle, you can determine the horizontal component of the acceleration.
Circular Motion
In the case of an object moving in a circular path, the horizontal acceleration can be calculated using the formula:
Ax = v²/r
Where:
– Ax is the horizontal acceleration (in m/s²)
– v is the tangential velocity of the object (in m/s)
– r is the radius of the circular path (in m)
This equation is derived from the centripetal acceleration formula, which describes the acceleration directed towards the center of the circular path. The horizontal acceleration is the component of the centripetal acceleration that is parallel to the ground.
Numerical Examples and Problem-Solving Strategies
To further solidify your understanding of horizontal acceleration, let’s explore some numerical examples and problem-solving strategies:
- Example 1: A car is traveling at a speed of 60 km/h and makes a turn with a radius of 50 m. Calculate the horizontal acceleration of the car.
Given:
– v = 60 km/h = 16.67 m/s
– r = 50 m
Ax = v²/r
Ax = (16.67 m/s)²/50 m
Ax = 5.56 m/s²
- Example 2: A block with a mass of 2 kg is pushed across a surface with a coefficient of kinetic friction of 0.3. If the applied force is 20 N, calculate the horizontal acceleration of the block.
Given:
– m = 2 kg
– μk = 0.3
– F = 20 N
Fk = μk * N
Fk = 0.3 * (2 kg * 9.81 m/s²)
Fk = 5.886 N
F – Fk = m * a
20 N – 5.886 N = 2 kg * a
a = 7.057 m/s²
These examples demonstrate the application of the various equations and techniques discussed earlier. By breaking down the problem, identifying the relevant variables, and applying the appropriate formulas, you can solve for the horizontal acceleration in a wide range of scenarios.
Conclusion
Mastering the concept of horizontal acceleration is crucial for understanding and analyzing the motion of objects in physics. This comprehensive guide has provided you with the necessary tools and knowledge to tackle a variety of horizontal acceleration problems, from the fundamental equation to more complex scenarios involving friction and circular motion.
By practicing the techniques and solving the numerical examples presented in this article, you will develop a strong foundation in calculating horizontal acceleration, which will serve you well in your physics studies and problem-solving endeavors.
Remember, the key to success in this field is a deep understanding of the underlying principles and a willingness to apply them in a systematic and logical manner. With dedication and practice, you will become proficient in finding horizontal acceleration and unlock a deeper appreciation for the fascinating world of physics.
References
- Calculating Horizontal Acceleration
- Calculating Horizontal Acceleration in Systems with Friction
- Horizontal Acceleration Calculator

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.