Comprehensive Guide: How to Find Energy with Voltage and Current

Summary

Electrical energy is a fundamental concept in physics, and understanding how to calculate it using voltage and current is crucial for many applications, from powering electronic devices to designing efficient electrical systems. This comprehensive guide will provide you with a deep dive into the theoretical foundations, practical applications, and advanced techniques for finding energy using voltage and current measurements.

Understanding Electrical Power and Energy

Electrical Power Formula

The foundation for finding energy with voltage and current is the formula for electrical power, which represents the rate at which electrical energy is transferred in an electric circuit. The formula for electrical power is:

P = V * I

where:
– P is the power in watts (W)
– V is the voltage in volts (V)
– I is the current in amperes (A)

Electrical Energy Formula

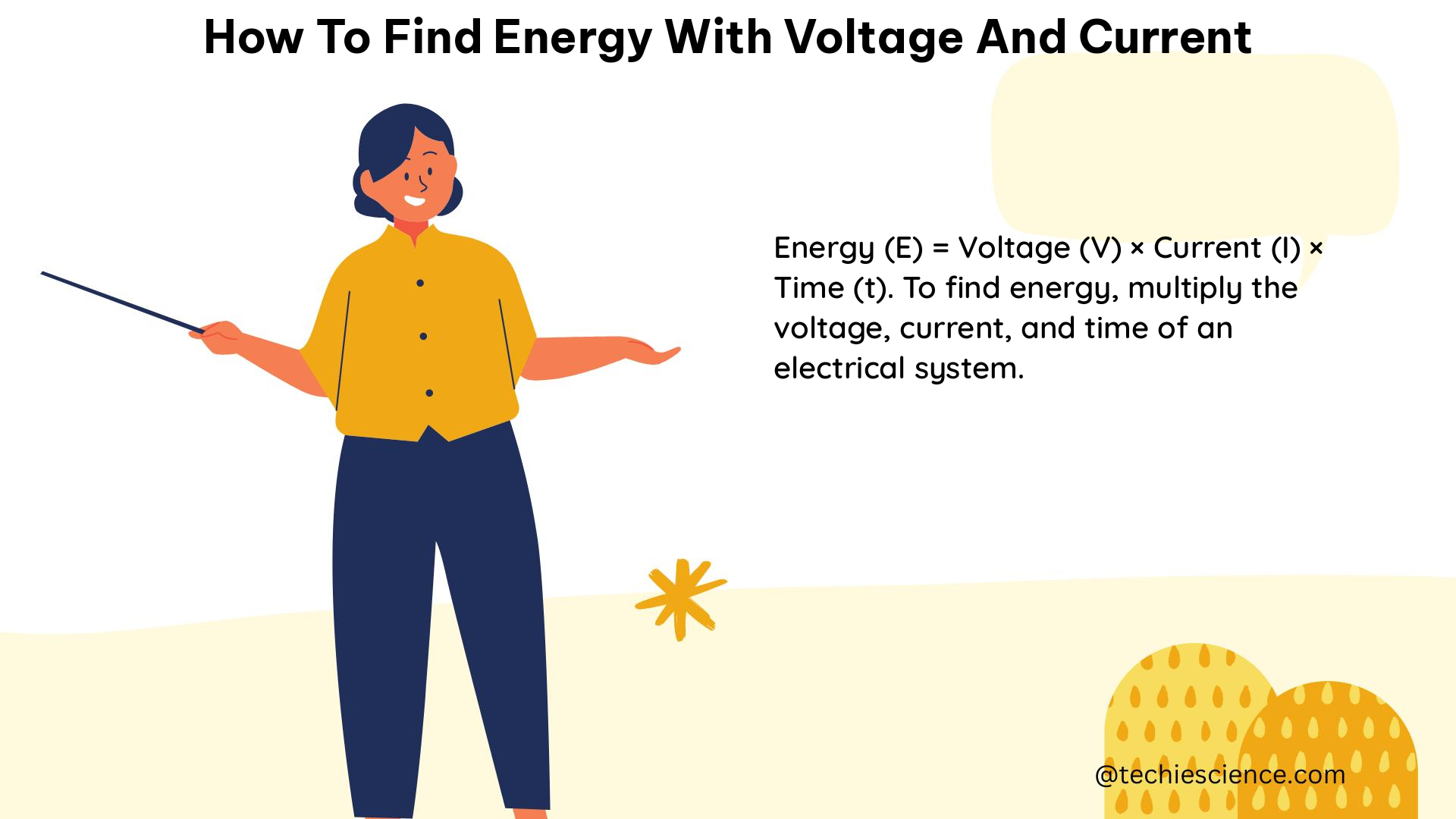
Once you have the power, you can calculate the electrical energy transferred over a given time period using the formula:

E = P * t

where:
– E is the energy in joules (J)
– P is the power in watts (W)
– t is the time in seconds (s)

Example Calculation

Let’s consider a circuit with a voltage of 10 volts and a current of 2 amperes. We can calculate the power and energy as follows:

1. Calculate the power:
   P = V * I
P = 10 V * 2 A
P = 20 watts

2. Calculate the energy transferred over 5 seconds:
   E = P * t
E = 20 W * 5 s
E = 100 joules

Therefore, the energy transferred in this circuit over a period of 5 seconds is 100 joules.

Factors Affecting Electrical Energy Calculations

Voltage and Current Direction

It’s important to note that the voltage and current must be measured in the same direction for the power to be positive. If they are measured in opposite directions, the power will be negative, indicating that energy is being transferred from the circuit to the source.

Capacitive Energy Storage

In addition to the power and energy formulas, there is another way to calculate the energy in a circuit, particularly for capacitors, which store energy in an electric field. The formula for the energy stored in a capacitor is:

E = 0.5 * C * V^2

where:
– E is the energy in joules (J)
– C is the capacitance in farads (F)
– V is the voltage in volts (V)

This formula is useful for understanding the energy storage capabilities of capacitors in electrical circuits.

Advanced Techniques and Considerations

Measuring Voltage and Current

Accurately measuring voltage and current is crucial for reliable energy calculations. Some common techniques include:
– Voltmeters for measuring voltage
– Ammeters for measuring current
– Multimeters for measuring both voltage and current

It’s important to ensure that the measurement devices are properly calibrated and connected to the circuit to obtain accurate readings.

Power Losses and Efficiency

In real-world electrical systems, there are often power losses due to factors such as resistance, heat generation, and other inefficiencies. These losses must be accounted for when calculating the actual energy transferred or consumed in the system. The efficiency of the system can be calculated as the ratio of the output power to the input power.

Electrical Energy Units and Conversions

Electrical energy is typically measured in joules (J), but it can also be expressed in other units, such as kilowatt-hours (kWh) or electron-volts (eV). Understanding the relationships between these units and being able to convert between them is essential for working with electrical energy calculations.

Electrical Energy Applications

Knowing how to calculate electrical energy is crucial in a wide range of applications, including:
– Powering electronic devices
– Designing electrical systems and circuits
– Analyzing energy consumption and efficiency
– Renewable energy systems (e.g., solar, wind)
– Electrical energy storage (e.g., batteries, capacitors)

Practical Examples and Numerical Problems

Example 1: Calculating Energy in a Resistive Circuit

Consider a resistive circuit with a voltage of 12 volts and a current of 3 amperes. Calculate the power and the energy transferred over a period of 10 seconds.

Given:
– Voltage, V = 12 V
– Current, I = 3 A
– Time, t = 10 s

Step 1: Calculate the power using the power formula.

P = V * I
P = 12 V * 3 A
P = 36 watts

Step 2: Calculate the energy transferred using the energy formula.

E = P * t
E = 36 W * 10 s
E = 360 joules

Therefore, the energy transferred in this resistive circuit over a period of 10 seconds is 360 joules.

Example 2: Calculating Energy in a Capacitive Circuit

A capacitor with a capacitance of 47 microfarads (μF) is charged to a voltage of 20 volts. Calculate the energy stored in the capacitor.

Given:
– Capacitance, C = 47 μF = 4.7 × 10^-5 F
– Voltage, V = 20 V

Step 1: Calculate the energy stored in the capacitor using the capacitive energy formula.

E = 0.5 * C * V^2
E = 0.5 * (4.7 × 10^-5 F) * (20 V)^2
E = 0.0094 joules

Therefore, the energy stored in the capacitor is 0.0094 joules.

Numerical Problems

1. A circuit has a voltage of 120 volts and a current of 5 amperes. Calculate the power and the energy transferred over a period of 1 minute.

2. A capacitor with a capacitance of 100 microfarads (μF) is charged to a voltage of 50 volts. Calculate the energy stored in the capacitor.

3. A resistor with a resistance of 1 kilohm (kΩ) is connected to a voltage source of 24 volts. Calculate the power dissipated in the resistor and the energy dissipated over a period of 30 seconds.

4. A solar panel has an output voltage of 18 volts and a current of 2.5 amperes. Calculate the power generated by the solar panel and the energy produced over a period of 2 hours.

5. A battery with a voltage of 9 volts and an internal resistance of 0.5 ohms (Ω) is connected to a load with a resistance of 2 ohms (Ω). Calculate the power delivered to the load and the energy delivered over a period of 15 minutes.

These examples cover a range of circuits and scenarios, allowing you to practice applying the concepts of electrical power and energy calculations using voltage and current measurements.

Conclusion

In this comprehensive guide, we have explored the fundamental principles and advanced techniques for finding energy with voltage and current. By understanding the power and energy formulas, the factors affecting electrical energy calculations, and the various practical applications, you now have a solid foundation to tackle a wide range of electrical energy problems.

Remember to always consider the direction of voltage and current, account for power losses and efficiency, and be familiar with the different units and conversions used in electrical energy calculations. With the knowledge and examples provided in this guide, you’ll be well-equipped to confidently apply these concepts in your physics studies and real-world electrical engineering applications.

References

1. Measurable Quantity – an overview | ScienceDirect Topics. (n.d.). Retrieved from https://www.sciencedirect.com/topics/engineering/measurable-quantity
2. How to Find Work (energy) from Voltage and Charge – YouTube. (n.d.). Retrieved from https://www.youtube.com/watch?v=XIMng8qmb7I
3. Potential difference | IOPSpark – Institute of Physics. (n.d.). Retrieved from https://spark.iop.org/collections/potential-difference