In the world of physics, understanding the relationship between the energy of a wave and its wavelength is crucial. Whether you’re studying electromagnetic radiation, sound waves, or any other type of wave phenomenon, being able to calculate the energy associated with a given wavelength can provide valuable insights. In this comprehensive guide, we’ll dive deep into the principles and formulas that govern this relationship, equipping you with the knowledge and tools to confidently determine the energy of a wave based on its wavelength.
Understanding the Energy-Wavelength Relationship
The energy associated with a wave is directly related to its wavelength, as described by the following formula:
E = 1/2 * μ * A^2 * ω^2 * λ
Where:
– E is the total energy associated with a wavelength of the wave
– μ is the linear mass density of the medium (for strings, this is the mass per unit length)
– A is the amplitude of the wave
– ω is the angular frequency of the wave
– λ is the wavelength of the wave
This formula represents the sum of the kinetic and potential energy associated with each wavelength of the wave. The kinetic energy is given by:
KE = 1/2 * μ * A^2 * ω^2
And the potential energy is given by:
PE = 1/2 * μ * A^2 * ω^2
The total energy is then the sum of these two components.
It’s important to note that this formula assumes a sinusoidal wave propagating in a string with a constant linear mass density. The formula can be modified for other types of waves and media, but the basic principles of energy conservation and wave motion still apply.
Calculating Energy for Waves in Different Media
Waves in Strings
For waves propagating in a string, the linear mass density (μ) is a crucial parameter. The linear mass density represents the mass per unit length of the string. By knowing the linear mass density, the amplitude of the wave, and the angular frequency, you can use the formula to calculate the total energy associated with a given wavelength.
Electromagnetic Waves
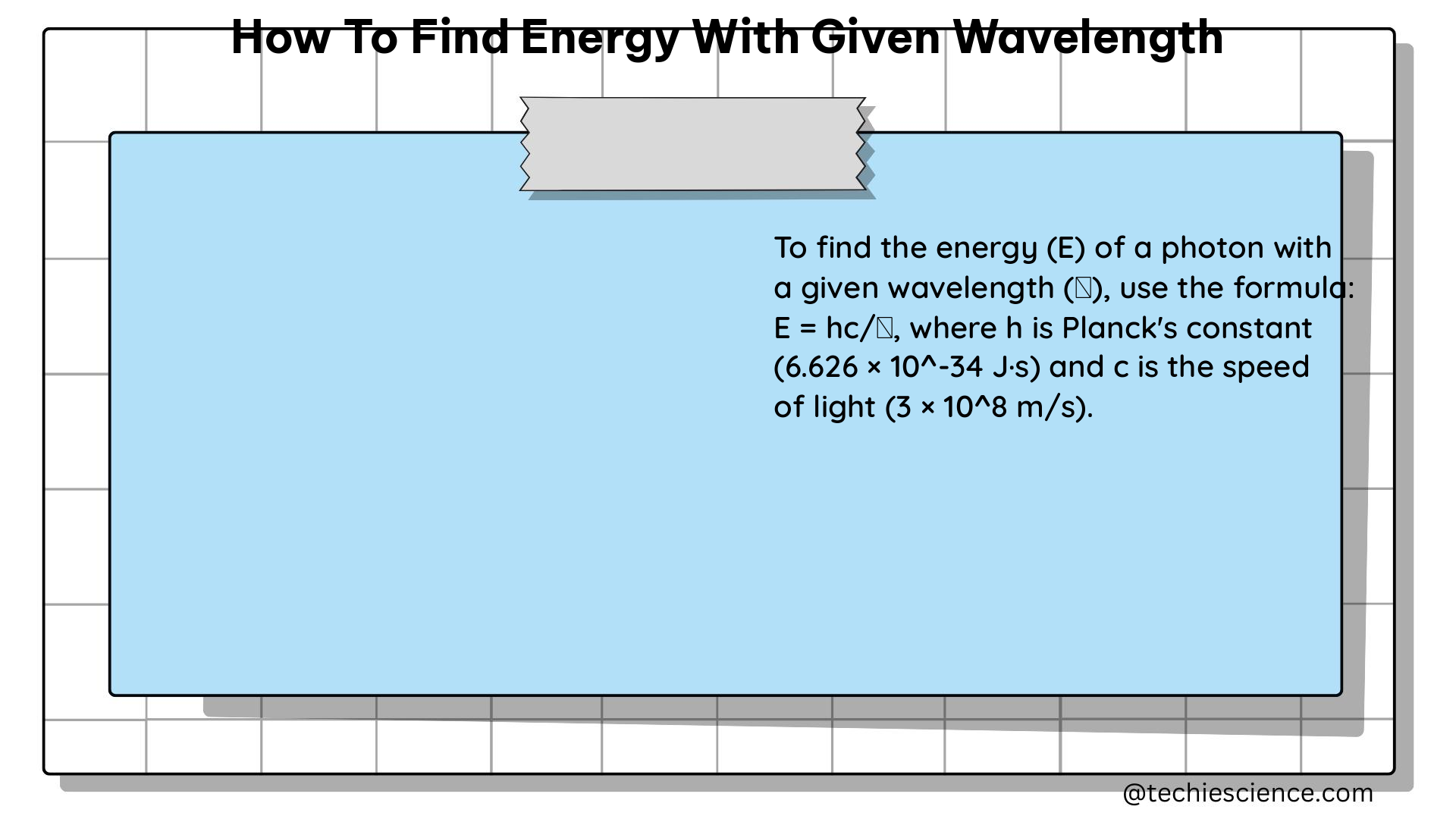
Electromagnetic waves, such as light, can also be described in terms of their wavelength and energy. In this case, we can use Planck’s equation to calculate the energy of a single photon:
E = h * c / λ
Where:
– E is the energy of a single photon
– h is Planck’s constant (6.626 x 10^-34 J * s)
– c is the speed of light (3 x 10^8 m/s)
– λ is the wavelength of the wave
This equation allows us to determine the energy of a single photon within an electromagnetic wave, given its wavelength.
Sound Waves
Sound waves, which are mechanical waves, can also be analyzed using the energy-wavelength relationship. In this case, the linear mass density (μ) would be replaced by the density of the medium (ρ) and the wave speed (v) would be used instead of the angular frequency (ω).
The formula for the total energy of a sound wave with a given wavelength would be:
E = 1/2 * ρ * A^2 * (2πv/λ)^2 * λ
Where:
– ρ is the density of the medium
– v is the speed of the sound wave
– λ is the wavelength of the sound wave
Example Calculations
Let’s go through some examples to illustrate how to apply the energy-wavelength formulas in different scenarios.
Example 1: Energy of a Wave in a String
Suppose we have a string with a linear mass density of 0.01 kg/m, vibrating with an amplitude of 0.05 m and a frequency of 5 Hz. What is the total energy associated with a wavelength of 10 m?
First, we need to calculate the angular frequency (ω):
ω = 2πf = 2π * 5 = 31.42 rad/s
Next, we can plug the values into the formula for total energy:
E = 1/2 * 0.01 * (0.05)^2 * (31.42)^2 * 10 = 0.395 J
Therefore, the total energy associated with a wavelength of 10 m in this string is 0.395 J.
Example 2: Energy of a Photon in a Light Wave
Consider a light wave with a wavelength of 500 nm and a frequency of 5 x 10^14 Hz. What is the energy of a single photon in this wave?
To calculate the energy of a single photon, we can use Planck’s equation:
E = h * c / λ
Where:
– h is Planck’s constant (6.626 x 10^-34 J * s)
– c is the speed of light (3 x 10^8 m/s)
– λ is the wavelength of the wave (500 x 10^-9 m)
Plugging in the values, we get:
E = (6.626 x 10^-34 J * s) * (3 x 10^8 m/s) / (500 x 10^-9 m) = 3.97 x 10^-19 J
Therefore, the energy of a single photon in this light wave is 3.97 x 10^-19 J.
Advanced Considerations
Dispersion and Frequency-Dependent Energy
In some cases, the energy-wavelength relationship may be more complex, particularly when dealing with dispersive media. Dispersion occurs when the wave speed (and consequently, the angular frequency) depends on the wavelength. In such scenarios, the energy-wavelength formula needs to be modified to account for the frequency-dependent nature of the wave properties.
Quantum Effects and Photon Energy
At the quantum level, the energy of electromagnetic waves is quantized, meaning it can only take on discrete values. This is the basis for the concept of photons, which are the fundamental particles of light. The energy of a photon is directly proportional to the frequency of the wave, as described by Planck’s equation.
Energy Density and Power
In addition to the total energy associated with a wavelength, it is often useful to consider the energy density and power of a wave. The energy density represents the energy per unit volume, while the power represents the energy per unit time. These quantities can be derived from the total energy formula and are important in various applications, such as the design of optical systems and the analysis of wave propagation.
Conclusion
Mastering the relationship between the energy and wavelength of waves is a crucial skill in the field of physics. By understanding the underlying principles and formulas, you can confidently calculate the energy associated with a given wavelength, whether it’s in the context of strings, electromagnetic waves, or sound waves. This knowledge will serve you well in your studies, research, and practical applications involving wave phenomena.
Remember, the key to success in this domain is a deep understanding of the fundamental concepts, coupled with the ability to apply the appropriate formulas and techniques to various scenarios. With the information provided in this comprehensive guide, you are well on your way to becoming an expert in determining the energy of waves based on their wavelengths.
References:
- OpenStax, University Physics Volume 1, Section 16.4: Energy and Power of a Wave
- Omni Calculator, Wavelength to Energy Calculator
- Study.com, Wavelength Formula & Calculation | How to Find Wavelength
- HyperPhysics, Energy and Wavelength of Photons
- Physics Stack Exchange, Relationship between energy and wavelength of a wave

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.