In the realm of physics, the relationship between the energy of a photon and its frequency is a fundamental concept that holds immense significance. This guide aims to provide a comprehensive and technical exploration of the methods and formulas used to determine the energy of a photon given its frequency, equipping you with the necessary knowledge and tools to navigate this fascinating domain.
Understanding the Equation: E = h * f
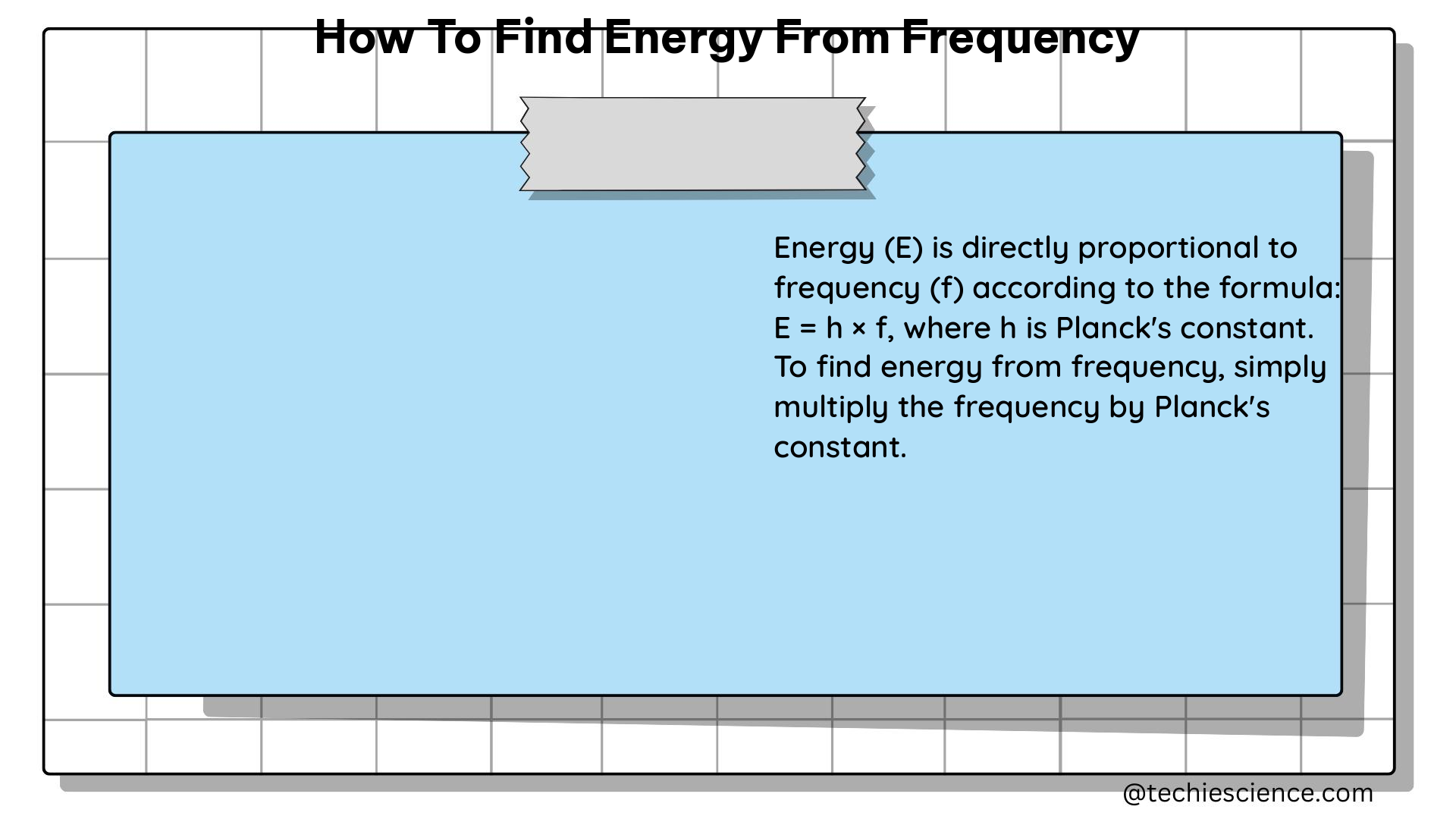
The equation that governs the relationship between the energy of a photon (E) and its frequency (f) is known as the Planck-Einstein equation, which states that E = h * f, where h is Planck’s constant, a fundamental physical constant with a value of 6.626 × 10^-34 Joule-seconds.
This equation is derived from the principles of quantum mechanics and the wave-particle duality of light, which suggests that light can exhibit both wave-like and particle-like properties. The energy of a photon is directly proportional to its frequency, meaning that photons with higher frequencies will have higher energies, and vice versa.
Calculating the Energy of a Photon
To calculate the energy of a photon given its frequency, you can simply plug the values into the Planck-Einstein equation:
E = h * f
Where:
– E is the energy of the photon, measured in Joules (J)
– h is Planck’s constant, which has a value of 6.626 × 10^-34 Joule-seconds (J·s)
– f is the frequency of the photon, measured in Hertz (Hz)
Let’s consider an example:
Suppose you have a photon with a frequency of 5 × 10^14 Hz. To calculate its energy, you would plug the values into the equation:
E = h * f
E = (6.626 × 10^-34 J·s) * (5 × 10^14 Hz)
E = 3.313 × 10^-19 Joules
This calculation demonstrates how the energy of a photon can be determined directly from its frequency using the Planck-Einstein equation.
Determining Frequency from Wavelength
In some cases, you may be given the wavelength of a photon instead of its frequency. To calculate the frequency, you can use the equation:
f = c / λ
Where:
– f is the frequency of the photon, measured in Hertz (Hz)
– c is the speed of light, which is approximately 3 × 10^8 meters per second (m/s)
– λ is the wavelength of the photon, measured in meters (m)
Let’s consider an example:
Suppose you have a photon with a wavelength of 600 nanometers (nm). To calculate its frequency, you would plug the values into the equation:
f = c / λ
f = (3 × 10^8 m/s) / (600 × 10^-9 m)
f = 5 × 10^14 Hz
Now that you have the frequency, you can use the Planck-Einstein equation to calculate the energy of the photon:
E = h * f
E = (6.626 × 10^-34 J·s) * (5 × 10^14 Hz)
E = 3.313 × 10^-19 Joules
Photon Energy and Frequency Relationships
The energy of a photon is directly proportional to its frequency, as described by the Planck-Einstein equation. This means that photons with higher frequencies will have higher energies, and photons with lower frequencies will have lower energies.
To illustrate this relationship, let’s consider some specific examples:
| Photon Frequency | Photon Energy |
|---|---|
| 400 THz (Visible Light) | 2.65 × 10^-19 Joules |
| 1000 THz (Ultraviolet Light) | 6.62 × 10^-19 Joules |
| 10 PHz (Gamma Rays) | 6.62 × 10^-15 Joules |
As you can see, the energy of the photon increases as the frequency increases. This relationship is fundamental to understanding the behavior of light and its interactions with matter.
Practical Applications and Considerations
The ability to determine the energy of a photon from its frequency has numerous practical applications in various fields, including:
- Spectroscopy: Analyzing the frequencies of light emitted or absorbed by atoms and molecules can provide valuable information about their electronic structure and energy levels.
- Photochemistry: Understanding the energy of photons is crucial in studying the interactions between light and chemical reactions, which is essential in fields like photosynthesis and photocatalysis.
- Medical Imaging: Techniques like X-ray and gamma-ray imaging rely on the high-energy photons to penetrate and interact with biological tissues, allowing for the visualization of internal structures.
- Renewable Energy: The development of photovoltaic cells and solar energy technologies depends on the efficient conversion of photon energy into electrical energy.
When working with photon energy and frequency, it’s important to consider the following factors:
- The units used for frequency (Hertz, Terahertz, Petahertz, etc.) and energy (Joules, electron-volts, etc.) and ensure consistent units throughout your calculations.
- The limitations of the Planck-Einstein equation, which assumes that the photon is a perfect, monochromatic wave. In reality, photons can exhibit more complex wave-particle behavior, especially at high energies or in the presence of strong electromagnetic fields.
- The potential for energy losses or transformations, such as through the absorption or scattering of photons, which can affect the overall energy balance in a system.
By understanding the fundamental principles and practical applications of the relationship between photon energy and frequency, you can unlock a deeper understanding of the behavior of light and its role in various scientific and technological domains.
References:
- How To Calculate The Energy of a Photon Given Frequency
- How to Convert Frequency to Energy
- Calculating the Energy of a Light Wave Given Frequency

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.