How to Find Energy Associated with Astronomical Phenomena

Summary

Determining the energy associated with astronomical phenomena involves leveraging physical laws like Stefan’s Law and mass-energy equivalence. By calculating the power radiated by an object and converting that power into mass, we can quantify the energy loss over time and gain insights into the object’s evolution and its impact on its surroundings.

Black Body Radiation and Stefan’s Law

The sun, as a black body, emits electromagnetic radiation across a wide spectrum, including visible light, UV rays, and other wavelengths. Stefan’s Law, also known as the Stefan-Boltzmann Law, provides a quantitative description of this emission. The law states that the power radiated from a black body is directly proportional to the fourth power of its absolute temperature and its surface area. This relationship highlights the sun’s intense energy output, as even small changes in temperature can lead to significant differences in energy emission.

The formula for the power radiated by a black body is:

Power = σ × A × T^4

Where:
– σ is the Stefan-Boltzmann constant (5.67 × 10^-8 W/m^2 K^4)
– A is the surface area of the object (e.g., the sun’s surface area is 6.09 × 10^18 m^2)
– T is the absolute temperature of the object in Kelvin (e.g., the sun’s surface temperature is approximately 5700 K)

By plugging in the values for the sun, we can calculate the power radiated by the sun:

Power = 5.67 × 10^-8 W/m^2 K^4 × 6.09 × 10^18 m^2 × (5700 + 273.15)^4
Power ≈ 3.85 × 10^26 W

This calculation demonstrates the immense power output of the sun, which is a crucial factor in understanding the energy associated with astronomical phenomena.

Mass-Energy Equivalence

In the context of the sun, mass-energy equivalence allows us to quantify the mass lost when energy is radiated away. The energy emitted as electromagnetic radiation, as calculated using Stefan’s Law, corresponds to a certain mass. Since energy and mass are equivalent, when the sun loses energy through radiation, it consequently loses mass.

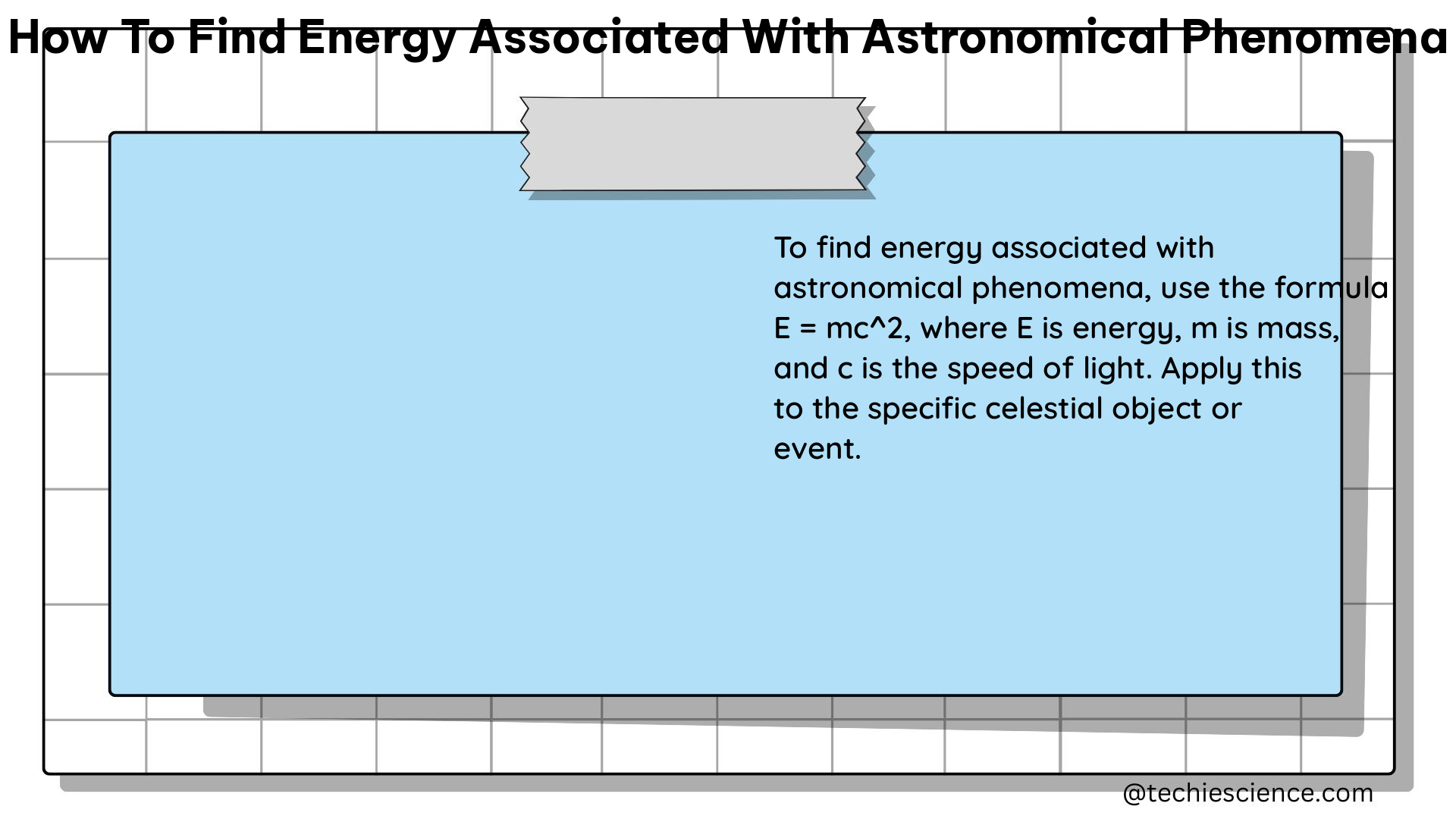
The relationship between energy and mass is given by the famous equation:

E = mc^2

Where:
– E is the energy
– m is the mass
– c is the speed of light (approximately 299,792,458 m/s)

By rearranging this equation, we can calculate the mass lost by the sun due to its radiation:

Mass loss per second = Power / (c^2)
Mass loss per second ≈ 3.85 × 10^26 W / (299,792,458 m/s)^2
Mass loss per second ≈ 4.28 × 10^9 kg/s

This calculation shows that the sun loses approximately 4.28 × 10^9 kg of mass every second due to radiation. While the individual loss may seem negligible, over astronomical timescales, this mass loss has significant implications for the sun’s evolution and the stability of the solar system.

Solar Mass Loss and Its Implications

The mass loss of the sun, as calculated using the power radiated and mass-energy equivalence, has profound implications for the sun’s lifecycle and the dynamics of the solar system.

Over time – years, centuries, and millennia – the sun’s continuous mass loss contributes to a measurable decrease in its overall mass. This mass loss affects the sun’s evolution, including changes in its luminosity, size, and ultimately, its transition to the later stages of its stellar life cycle.

Understanding the sun’s mass loss is not only important for astrophysics but also for our insight into the stability and longevity of the solar system. As the sun loses mass, the gravitational forces within the solar system are affected, potentially leading to changes in the orbits of the planets and other celestial bodies.

By quantifying the energy associated with the sun’s radiation and the corresponding mass loss, scientists can better predict and model the long-term behavior of the solar system, which is crucial for understanding the past, present, and future of our cosmic neighborhood.

Applying the Principles to Other Astronomical Phenomena

The principles and methods used to find the energy associated with the sun’s radiation can be applied to other astronomical phenomena as well. For example, the same approach can be used to determine the energy output and mass loss of other stars, exoplanets, and even more exotic objects like black holes and neutron stars.

By understanding the energy associated with these astronomical phenomena, scientists can gain valuable insights into their physical properties, evolution, and interactions with their surrounding environments. This knowledge is essential for advancing our understanding of the universe and its complex dynamics.

Conclusion

In summary, to find the energy associated with astronomical phenomena, we need to leverage physical laws like Stefan’s Law and mass-energy equivalence. By calculating the power radiated by an object and converting that power into mass, we can quantify the energy loss over time and use this information to understand the object’s evolution and its impact on its surroundings.

This approach, as demonstrated through the example of the sun, provides a powerful tool for exploring the energy dynamics of various astronomical objects and phenomena. As we continue to expand our knowledge of the universe, the ability to accurately determine the energy associated with these phenomena will be crucial for advancing our understanding of the cosmos.

References:

• Calculate the Power Radiated by the Sun Using Stefan’s Law – Vaia
• 1.1 The Scope and Scale of Physics – UCF Pressbooks
• Astronomical Research – an overview | ScienceDirect Topics
• Solar Particle Events and Radiation Exposure in Space. Hu S. – NASA
• Astronomy is better with better statistics | Eberly College of Science