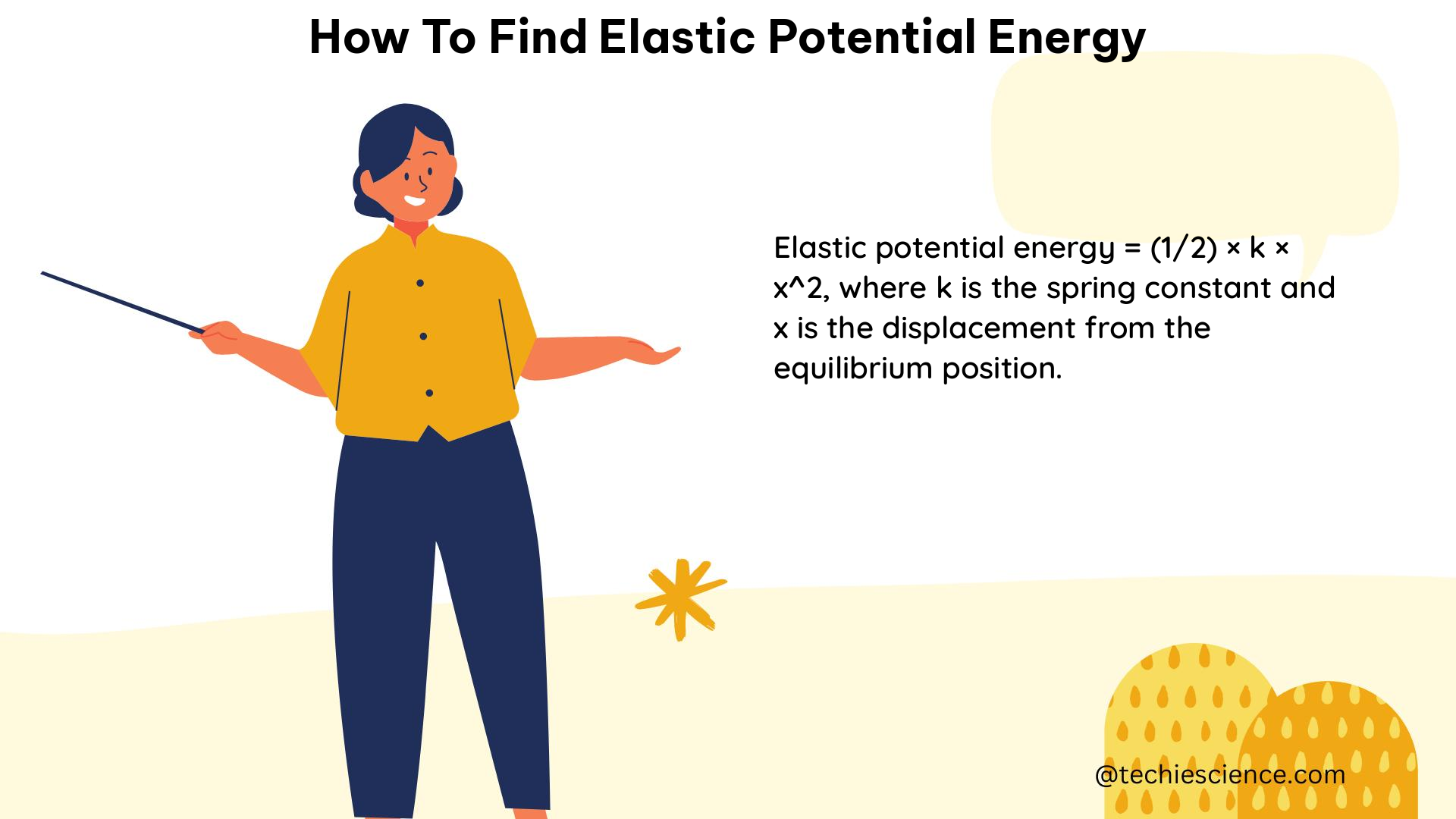
Elastic potential energy is the energy stored in an object due to its deformation or change in shape. It is a crucial concept in physics, particularly in the study of mechanics and the behavior of materials under stress. To find the elastic potential energy, you can use the formula PE = 0.5 * k * x², where PE is the elastic potential energy, k is the spring constant, and x is the displacement of the spring from its equilibrium position.
Understanding the Elastic Potential Energy Formula
The elastic potential energy formula is derived from Hooke’s law, which states that the force required to stretch or compress a spring is proportional to the distance of the displacement. The formula can be expressed as:
PE = 0.5 * k * x²
Where:
– PE is the elastic potential energy (in Joules, J)
– k is the spring constant (in Newtons per meter, N/m)
– x is the displacement of the spring from its equilibrium position (in meters, m)
The factor of 0.5 in the formula is due to the fact that the potential energy stored in the spring is proportional to the work done in stretching or compressing the spring, which is given by the area under the force-displacement curve.
Calculating the Spring Constant (k)
The spring constant, k, is a measure of the stiffness of the spring. It is the ratio of the force applied to the spring and the resulting displacement. The spring constant can be determined experimentally or using the following formula:
k = F / x
Where:
– F is the force applied to the spring (in Newtons, N)
– x is the displacement of the spring (in meters, m)
The spring constant is typically expressed in units of Newtons per meter (N/m).
Measuring the Displacement (x)
The displacement, x, is the distance that the spring is stretched or compressed from its equilibrium position. It is typically measured in meters (m) or millimeters (mm).
To measure the displacement, you can use a ruler or a caliper to determine the distance between the spring’s current position and its equilibrium position.
Calculating Elastic Potential Energy: Examples
Let’s consider a few examples to illustrate how to calculate the elastic potential energy.
Example 1: Stretching a Spring
Suppose you have a spring with a spring constant of 50 N/m, and you stretch it to a displacement of 0.1 m from its equilibrium position. To calculate the elastic potential energy, you can use the formula:
PE = 0.5 * k * x²
PE = 0.5 * 50 N/m * (0.1 m)²
PE = 0.5 * 50 * 0.01
PE = 0.25 Joules (J)
Therefore, the elastic potential energy stored in the spring is 0.25 Joules.
Example 2: Compressing a Spring
Now, let’s consider a spring with a spring constant of 80 N/m, and you compress it to a displacement of 0.05 m from its equilibrium position. To calculate the elastic potential energy, you can use the formula:
PE = 0.5 * k * x²
PE = 0.5 * 80 N/m * (0.05 m)²
PE = 0.5 * 80 * 0.0025
PE = 0.1 Joules (J)
In this case, the elastic potential energy stored in the spring is 0.1 Joules.
Using Elastic Potential Energy Calculators
To simplify the calculation of elastic potential energy, you can use online calculators or apps. These tools allow you to input the known variables (spring constant and displacement) and automatically calculate the elastic potential energy.
Some popular elastic potential energy calculators include:
– Elastic Potential Energy Calculator
– Elastic Potential Energy Omnicalculator
These calculators can be particularly useful when you need to find the missing variable in the elastic potential energy equation, such as the spring constant or the displacement, given the other two variables.
Limitations and Considerations
It’s important to note that the elastic potential energy formula is valid only for small deformations, where the material behaves linearly and follows Hooke’s law. For larger deformations, the relationship between force and displacement may become non-linear, and the formula may not accurately represent the stored energy.
Additionally, the elastic potential energy is always positive, as it represents the amount of energy required to deform the object from its equilibrium position. Negative values of elastic potential energy are not physically meaningful.
Conclusion
In summary, to find the elastic potential energy, you need to know the spring constant and the displacement of the spring from its equilibrium position. By using the formula PE = 0.5 * k * x², you can calculate the amount of energy stored in the spring due to its deformation. Understanding the concept of elastic potential energy is crucial in various fields of physics, engineering, and material science, as it helps to analyze the behavior of materials under stress and predict their response to applied forces.
References
- Hooke’s Law and Elastic Potential Energy: https://www.physicsclassroom.com/class/waves/Lesson-0/Motion-of-a-Mass-on-a-Spring
- Calculating Elastic Potential Energy: https://www.ck12.org/flexi/physical-science/potential-energy/what-is-the-equation-for-calculating-elastic-potential-energy/
- Elastic Potential Energy Calculator: https://www.calculatorsoup.com/calculators/physics/elastic-potential.php
- Elastic Potential Energy Omnicalculator: https://www.omnicalculator.com/physics/elastic-potential-energy

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.