How To Find Constant Acceleration With Distance And Time:Problems And Examples

When studying motion and the principles of physics, understanding how to find constant acceleration with distance and time is crucial. Acceleration is a fundamental concept in physics that measures how quickly an object’s velocity changes over time. By knowing the distance traveled and the time taken, we can calculate the object’s constant acceleration. In this blog post, we will explore the relationship between acceleration, distance, and time, and learn how to calculate constant acceleration using simple formulas and step-by-step instructions.

The Relationship between Acceleration, Distance, and Time

The Role of Distance in Acceleration

Distance plays a vital role in calculating acceleration. The formula for acceleration is derived by dividing the change in velocity by the change in time. However, when considering constant acceleration, we can utilize the formula that relates distance, initial velocity, final velocity, and time:

$d = \frac{1}{2}(v_0 + v)t$

In this equation, $d$ represents the distance traveled, $v_0$ is the initial velocity, $v$ is the final velocity, and $t$ is the time taken. By rearranging this formula, we can solve for acceleration.

The Role of Time in Acceleration

constant acceleration with distance and time 2

Time is a crucial factor when calculating acceleration. The acceleration of an object depends on how quickly its velocity changes over a given period. By dividing the change in velocity by the change in time, we can determine the average acceleration. However, for constant acceleration, we can use the formula:

$a = \frac{v - v_0}{t}$

In this equation, $a$ represents the acceleration, $v$ is the final velocity, $v_0$ is the initial velocity, and $t$ is the time taken. This formula allows us to calculate the acceleration of an object when the initial and final velocities and the time are known.

The Interplay between Distance, Time, and Acceleration

Distance, time, and acceleration are interconnected when studying the motion of an object. Acceleration determines how quickly an object’s velocity changes over time. By measuring the distance traveled and the time taken, we can calculate the acceleration. Conversely, knowing the acceleration and the time, we can determine the distance traveled.

How to Calculate Constant Acceleration with Distance and Time

how to find constant acceleration with distance and time — Image by P. Fraundorf – Wikimedia Commons, Licensed under CC BY-SA 4.0.

To calculate constant acceleration using the given distance and time, follow these steps:

Step 1: Gather the required information

Before calculating constant acceleration, make sure you have the following information:
– Initial velocity $\(v_0$ )
– Final velocity $\(v$ )
– Time taken $\(t$ )

Step 2: Use the formula for constant acceleration

The formula to calculate constant acceleration is:

$a = \frac{v - v_0}{t}$

Substitute the values you have into the formula.

Step 3: Solve for acceleration

constant acceleration with distance and time 3

With the values plugged into the formula, solve for acceleration. The resulting value will give you the constant acceleration of the object.

Worked Out Examples of Calculating Constant Acceleration

Let’s look at a couple of examples to better understand how to calculate constant acceleration using distance and time.

Example 1:

Suppose a car starts from rest and reaches a velocity of 30 m/s in 5 seconds. Calculate the constant acceleration.

Given:
Initial velocity $\(v_0$ ) = 0 m/s
Final velocity $\(v$ ) = 30 m/s
Time taken $\(t$ ) = 5 s

Using the formula:
$a = \frac{v - v_0}{t}$

Substituting the given values:
$a = \frac{30 - 0}{5}$

Simplifying the expression:
$a = \frac{30}{5}$
$a = 6 \, \text{m/s}^2$

Therefore, the constant acceleration of the car is 6 m/s².

Example 2:

A stone is thrown vertically upward with an initial velocity of 20 m/s. If it reaches a height of 40 m, calculate the constant acceleration.

Given:
Initial velocity $\(v_0$ ) = 20 m/s (upward direction)
Final velocity $\(v$ ) = 0 m/s (at its highest point)
Time taken $\(t$ ) = ?

To find the time taken, we can use the formula for displacement in the vertical motion:

$d = v_0t + \frac{1}{2}at^2$

At the highest point, the displacement is 40 m, the initial velocity is 20 m/s, and the final velocity is 0 m/s. We can rearrange the formula to solve for time:

$t = \frac{-v_0 \pm \sqrt{v_0^2 - 4(\frac{1}{2}a)(-d)}}{2(\frac{1}{2}a)}$

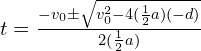
Substituting the given values:
$t = \frac{-20 \pm \sqrt{20^2 - 4(\frac{1}{2}a)(-40)}}{2(\frac{1}{2}a)}$

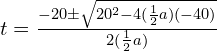
Simplifying the expression:
$t = \frac{-20 \pm \sqrt{400 + 40a}}{a}$

To determine the sign in front of the square root, we can deduce that the time taken will be a positive value. Therefore, we can ignore the negative sign.

Now, substitute the displacement $\(d$ ) as 40 m, and rearrange the formula to solve for acceleration:

$a = \frac{v - v_0}{t}$

Given:
Initial velocity $\(v_0$ ) = 20 m/s
Final velocity $\(v$ ) = 0 m/s
Time taken $\(t$ ) = 2s (approximated value)

Substituting the given values:
$a = \frac{0 - 20}{2}$

Simplifying the expression:
$a = \frac{-20}{2}$
$a = -10 \, \text{m/s}^2$

Therefore, the constant acceleration of the stone is approximately -10 m/s².

Common Mistakes and Misconceptions in Calculating Constant Acceleration

It is essential to be aware of common mistakes and misconceptions when calculating constant acceleration. Here are a few to watch out for:

Common Errors in Using the Formula

Forgetting to consider the direction of velocity when calculating acceleration. Velocity is a vector quantity that includes both magnitude and direction. Neglecting the signs or getting the signs wrong can lead to incorrect results.
Failing to convert units consistently. Make sure all values used in the formula have the same units (e.g., meters per second or seconds). Inconsistent units can result in erroneous calculations.
Not using the correct formula. Depending on the given information, the formulas for acceleration may vary. Always ensure you are using the appropriate formula for the specific scenario.

Misconceptions about Constant Acceleration

Assuming that constant acceleration always means the object is moving in a straight line. While constant acceleration often occurs in linear motion, it can also apply to circular or curved paths.
Believing that constant acceleration implies constant velocity. In reality, constant acceleration means that the rate at which the velocity changes remains the same, but the actual velocity can vary over time.

Tips to Avoid Mistakes in Calculating Constant Acceleration

To minimize errors and misconceptions when calculating constant acceleration, keep the following tips in mind:

Pay attention to the direction of velocity and acceleration when working with vector quantities.
Double-check units and ensure consistency throughout the calculations.
Take into account the specific scenario and select the appropriate formula for calculating acceleration.
Use diagrams or graphs to visualize the motion and aid in understanding the problem.
Practice solving various problems involving constant acceleration to strengthen your understanding and proficiency.

By being aware of these common mistakes and misconceptions, you can improve your accuracy when calculating constant acceleration and gain a deeper understanding of the concept.

Numerical Problems on how to find constant acceleration with distance and time

Problem 1:

Image by SweetWood – Wikimedia Commons, Wikimedia Commons, Licensed under CC0.

constant acceleration with distance and time 1

A car accelerates uniformly from rest to a velocity of 20 m/s in a time of 10 seconds. Calculate the acceleration of the car.

Solution:

Given:
Initial velocity, $u = 0 \, \text{m/s}$
Final velocity, $v = 20 \, \text{m/s}$
Time taken, $t = 10 \, \text{seconds}$

We can use the formula to find acceleration:
$a = \frac{v - u}{t}$

Substituting the given values, we get:
$a = \frac{20 - 0}{10}$

$a = \frac{20}{10}$

$a = 2 \, \text{m/s}^2$

Therefore, the acceleration of the car is $2 \, \text{m/s}^2$ .

Problem 2:

A train starts from rest and accelerates uniformly at a rate of $4 \, \text{m/s}^2$ for a distance of 500 meters. Find the time taken by the train to cover this distance.

Solution:

Given:
Acceleration, $a = 4 \, \text{m/s}^2$
Distance, $s = 500 \, \text{m}$

We can use the formula to find time:
$s = ut + \frac{1}{2}at^2$

Since the train starts from rest, the initial velocity $\(u$ ) is 0. Therefore, the equation becomes:
$s = \frac{1}{2}at^2$

Substituting the given values, we get:
$500 = \frac{1}{2} \cdot 4 \cdot t^2$

Simplifying the equation, we have:
$500 = 2t^2$

Dividing both sides of the equation by 2, we get:
$250 = t^2$

Taking the square root of both sides, we get:
$t = \sqrt{250}$

Therefore, the time taken by the train to cover the distance is $\sqrt{250}$ seconds.

Problem 3:

A stone is thrown vertically upward with an initial velocity of 30 m/s. Determine the maximum height reached by the stone and the time taken to reach this height. $Consider acceleration due to gravity as \(-9.8 \, \text{m/s}^2$ )

Solution:

Given:
Initial velocity, $u = 30 \, \text{m/s}$
Acceleration due to gravity, $a = -9.8 \, \text{m/s}^2$

To find the time taken to reach the maximum height, we can use the formula:
$v = u + at$

Since the stone is thrown vertically upward, the final velocity $\(v$ ) at the maximum height is 0. Therefore, the equation becomes:
$0 = 30 - 9.8t$

Simplifying the equation, we have:
$30 = 9.8t$

Dividing both sides of the equation by 9.8, we get:
$t = \frac{30}{9.8}$

Next, we can find the maximum height $\(h$ ) reached by the stone using the formula:
$h = ut + \frac{1}{2}at^2$

Substituting the values of $u$ , $a$ , and $t$ , we get:
$h = 30 \cdot \frac{30}{9.8} + \frac{1}{2} \cdot (-9.8) \cdot \left(\frac{30}{9.8}\right)^2$

Simplifying the equation, we have:
$h = \frac{900}{9.8} - \frac{1}{2} \cdot 9.8 \cdot \left(\frac{900}{9.8}\right)$

$h = 91.84 - 450$

$h = -358.16$

Since the stone is thrown vertically upward, the maximum height reached by the stone is 358.16 meters above the initial position. The negative sign indicates that the stone is below the initial position.

The time taken to reach this height is $\frac{30}{9.8}$ seconds.

Also Read:

Keerthi Murthi

I am Keerthi K Murthy, I have completed post graduation in Physics, with the specialization in the field of solid state physics. I have always consider physics as a fundamental subject which is connected to our daily life. Being a science student I enjoy exploring new things in physics. As a writer my goal is to reach the readers with the simplified manner through my articles.