How to Find Centripetal Acceleration Without Radius: A Comprehensive Guide

Centripetal acceleration is a crucial concept in physics, describing the acceleration experienced by an object moving in a circular path. While the formula for centripetal acceleration typically includes the radius of the circular motion, there are situations where the radius may not be known or readily available. In such cases, you can still determine the centripetal acceleration using alternative methods. This comprehensive guide will walk you through the step-by-step process of finding centripetal acceleration without the radius.

Understanding Centripetal Acceleration

Centripetal acceleration is the acceleration experienced by an object moving in a circular path, directed towards the center of the circle. The formula for centripetal acceleration is:

a = ω²r

where:
– a is the centripetal acceleration
– ω is the angular velocity
– r is the radius of the circular motion

However, if the radius r is not given, you can still find the centripetal acceleration using other known variables.

Finding Centripetal Acceleration Without Radius

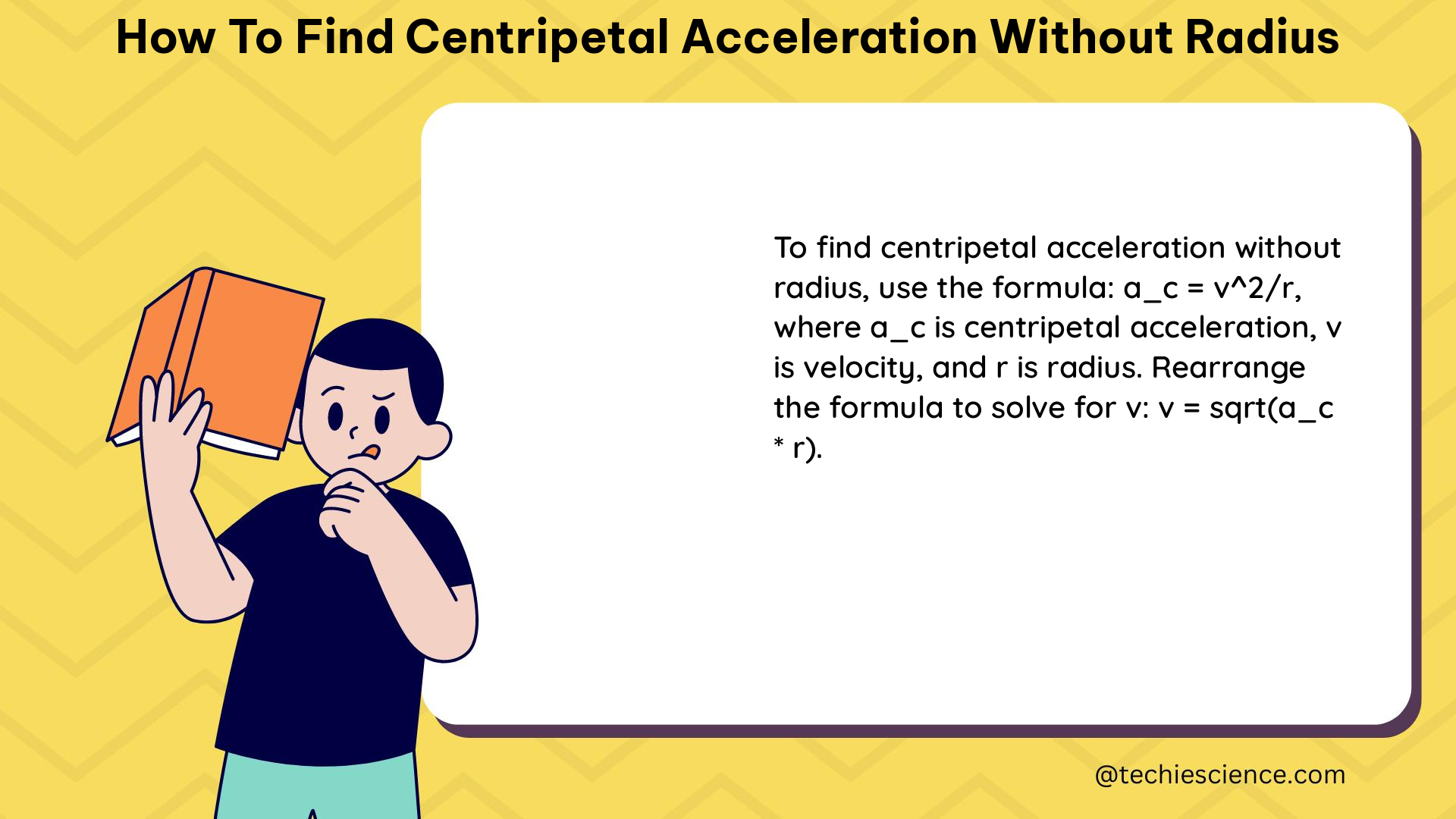
To find the centripetal acceleration without the radius, you can use the following alternative formula:

a = v²/r

where:
– a is the centripetal acceleration
– v is the linear velocity of the object
– r is the radius of the circular motion

To use this formula, you need to know the linear velocity v of the object and the period T of the circular motion. You can then calculate the radius r using the formula:

r = vT/2π

Once you have the radius r, you can substitute it into the formula a = v²/r to find the centripetal acceleration.

Example Calculation

Let’s consider an example to illustrate the process:

Suppose an object is moving in a circular path with a linear velocity of 10 m/s and a period of 2 seconds.

1. Calculate the radius r using the formula r = vT/2π:
   r = (10 m/s)(2 s)/(2π) = 1.59 m

2. Calculate the centripetal acceleration a using the formula a = v²/r:
   a = (10 m/s)²/1.59 m = 62.1 m/s²

Therefore, the centripetal acceleration of the object is 62.1 m/s².

Theoretical Foundations

The relationship between centripetal acceleration, angular velocity, and radius is derived from the fundamental principles of circular motion. The centripetal acceleration is the result of the constant change in the direction of the velocity vector, which is perpendicular to the velocity itself.

The formula a = ω²r can be proven using calculus and the concept of instantaneous velocity. The derivation involves considering the change in velocity over a small time interval and taking the limit as the time interval approaches zero.

Similarly, the formula a = v²/r can be derived by substituting the relationship v = ωr into the original formula a = ω²r.

Advanced Techniques and Considerations

1. Circular Motion with Varying Radius: In some cases, the radius of the circular motion may not be constant. In such situations, you can use the formula a = v²/r and calculate the radius at each point along the circular path to determine the centripetal acceleration.

2. Non-Uniform Circular Motion: When the angular velocity is not constant, the centripetal acceleration can be calculated using the formula a = dv/dt, where dv is the change in velocity and dt is the change in time.

3. Centripetal Force and Centrifugal Force: Centripetal acceleration is related to the centripetal force, which is the force that causes the object to move in a circular path. The centrifugal force, on the other hand, is an apparent force that acts on the object in the opposite direction of the centripetal force.

4. Applications in Physics and Engineering: Centripetal acceleration is a fundamental concept in various fields, such as mechanics, astronomy, and engineering. Understanding how to find centripetal acceleration without the radius is crucial in analyzing the motion of objects in circular paths, such as satellites, planets, and rotating machinery.

Conclusion

In summary, this comprehensive guide has provided you with the necessary tools and techniques to find centripetal acceleration without the radius. By understanding the alternative formulas and the underlying theoretical foundations, you can now confidently solve problems involving circular motion, even when the radius is not directly given. Remember to practice applying these methods to a variety of scenarios to solidify your understanding of this important concept in physics.

Reference:

1. Proof of Centripetal Acceleration Formula (without Calculus)
2. How to Calculate the Centripetal Acceleration of an Object Using Angular Velocity
3. Calculating Centripetal Acceleration | Physics – Study.com