How to Find Centripetal Acceleration with Radius and Time: A Comprehensive Guide

Centripetal acceleration is a crucial concept in physics, describing the acceleration experienced by an object moving in a circular path. To calculate centripetal acceleration, you need to know the object’s linear velocity, radius of the circular path, and angular velocity. In this comprehensive guide, we’ll dive deep into the formulas, measurements, and examples to help you master the art of finding centripetal acceleration with radius and time.

Understanding Centripetal Acceleration Formulas

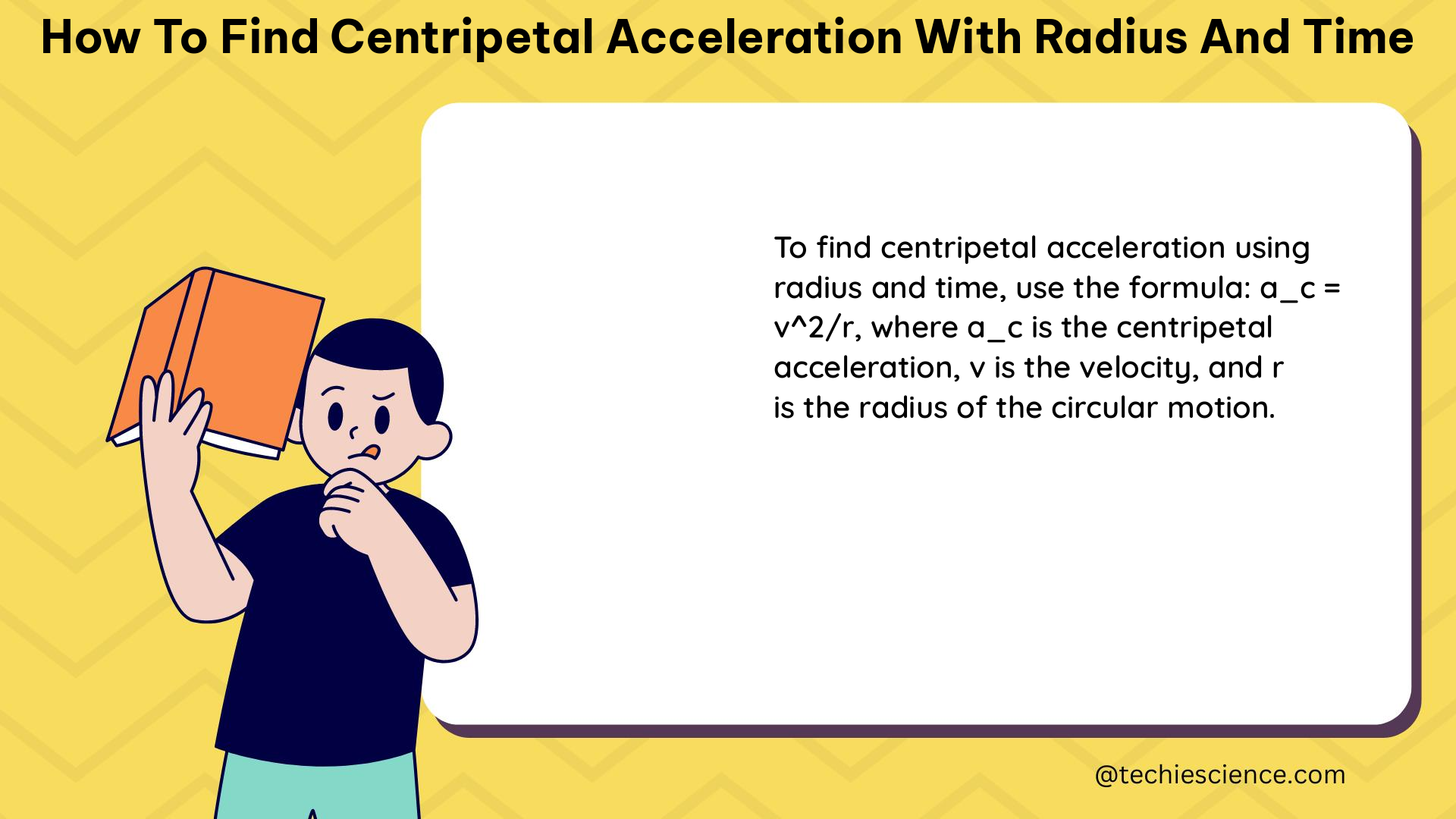
The two main formulas used to calculate centripetal acceleration are:

1. a⃗ = v⃗/t
2. a⃗ = rω²

Where:
– a⃗ is the centripetal acceleration (in m/s²)
– v⃗ is the linear velocity (in m/s)
– t is the time (in s)
– r is the radius of the circular path (in m)
– ω is the angular velocity (in rad/s)

These formulas are derived from the fundamental principles of circular motion and can be used to determine the centripetal acceleration of an object moving in a circular path.

Measuring Linear Velocity (v⃗)

To measure the linear velocity of an object, you can use a stopwatch to record the time it takes for the object to cover a known distance. Then, you can use the formula:

v⃗ = d/t

Where:
– v⃗ is the linear velocity (in m/s)
– d is the distance covered (in m)
– t is the time taken to cover the distance (in s)

For example, if an object covers a distance of 20 meters in 5 seconds, its linear velocity would be:

v⃗ = 20 m / 5 s = 4 m/s

Measuring Radius (r)

To measure the radius of the circular path, you can use a measuring tape or a ruler to determine the distance from the center of the circular path to the object. This distance represents the radius (r) of the circular path.

For instance, if the object is moving in a circular path with a radius of 3 meters, then r = 3 m.

Measuring Angular Velocity (ω)

To measure the angular velocity of an object, you can use a protractor to measure the angle (θ) subtended by the object at the center of the circular path over a certain time (t). Then, you can use the formula:

ω = θ/t

Where:
– ω is the angular velocity (in rad/s)
– θ is the angle subtended by the object (in rad)
– t is the time taken to cover the angle (in s)

For example, if an object subtends an angle of 0.5 radians at the center of the circular path in 2 seconds, its angular velocity would be:

ω = 0.5 rad / 2 s = 0.25 rad/s

Calculating Centripetal Acceleration

Once you have the values for linear velocity (v⃗), radius (r), and angular velocity (ω), you can use the formulas to calculate the centripetal acceleration (a⃗).

Example 1: Calculating Centripetal Acceleration using a⃗ = v⃗²/r

Suppose an object is moving in a circular path with a radius of 2 meters and a linear velocity of 4 m/s. To find the centripetal acceleration, we can use the formula:

a⃗ = v⃗²/r
a⃗ = (4 m/s)² / 2 m
a⃗ = 8 m/s²

Therefore, the centripetal acceleration of the object is 8 m/s².

Example 2: Calculating Centripetal Acceleration using a⃗ = rω²

Now, let’s consider an object moving in a circular path with a radius of 3 meters and an angular velocity of 2 rad/s. We can use the formula:

a⃗ = rω²
a⃗ = 3 m * (2 rad/s)²
a⃗ = 12 m/s²

In this case, the centripetal acceleration of the object is 12 m/s².

Practical Applications and Considerations

Centripetal acceleration is a fundamental concept in various fields, including:

• Circular motion in sports (e.g., racing, figure skating)
• Satellite orbits and planetary motion
• Centrifugal force and its applications (e.g., centrifuges, washing machines)
• Rotational dynamics in machinery and engineering

When working with centripetal acceleration, it’s important to consider the following:

1. Uniform Circular Motion: The formulas presented in this guide assume that the object is moving in a circular path with a constant speed (uniform circular motion). If the speed is not constant, the analysis becomes more complex.
2. Coordinate Systems: Centripetal acceleration is a vector quantity, so it’s essential to consider the appropriate coordinate system (e.g., Cartesian, polar) when working with the formulas.
3. Limitations and Assumptions: The formulas and examples provided in this guide are based on certain assumptions and simplifications. In real-world scenarios, additional factors may need to be considered, such as air resistance, friction, or the effects of gravity.

Conclusion

Mastering the art of finding centripetal acceleration with radius and time is a crucial skill for physics students and professionals. By understanding the formulas, learning how to measure the necessary parameters, and working through practical examples, you can develop a solid foundation in this fundamental concept of circular motion. Remember to always consider the underlying assumptions and limitations when applying these principles in real-world situations.

References

1. Centripetal Force – Notre Dame: https://www3.nd.edu/~pkamat/pdf/centripetal.pdf
2. Calculating Centripetal Acceleration – Study.com: https://study.com/academy/lesson/calculating-centripetal-acceleration.html
3. Problem 87: A particle’s centripetal acceleration is amathrmc4 – Vaia: https://www.vaia.com/problem-87-a-particles-centripetal-acceleration-is/
4. Centripetal Acceleration – Lumen Learning: https://courses.lumenlearning.com/physics/chapter/6-2-uniform-circular-motion/
5. 6.2 Uniform Circular Motion – Physics | OpenStax: https://openstax.org/books/university-physics-volume-1/pages/6-2-uniform-circular-motion