How to Find Binding Energy from Mass Defect: A Comprehensive Guide

The binding energy of a nucleus is the energy required to separate the nucleus into its individual protons and neutrons. This energy is directly related to the mass defect, which is the difference between the actual mass of the nucleus and the sum of the masses of its constituent particles. By understanding the relationship between mass defect and binding energy, we can determine the binding energy of a nucleus using the principles of nuclear physics.

Understanding Mass Defect

The mass defect of a nucleus is the difference between the actual mass of the nucleus and the sum of the masses of its constituent protons and neutrons. This mass defect is a result of the strong nuclear force that binds the nucleons (protons and neutrons) together within the nucleus.

The formula for calculating the mass defect is:

Mass Defect = (Z × m_p) + (N × m_n) – m_nucleus

Where:
– Z is the number of protons in the nucleus
– m_p is the mass of a proton
– N is the number of neutrons in the nucleus
– m_n is the mass of a neutron
– m_nucleus is the actual mass of the nucleus

For example, let’s consider the case of the Oxygen-16 (16O) nucleus, which has 8 protons and 8 neutrons.

The theoretical mass of the 16O nucleus can be calculated as:
– (8 × 1.007276 u) + (8 × 1.008665 u) = 16.13192 u

The actual mass of the 16O nucleus is given as 15.9905 u.

Therefore, the mass defect of the 16O nucleus is:
– Mass Defect = 16.13192 u – 15.9905 u = 0.14142 u

Converting Mass Defect to Binding Energy

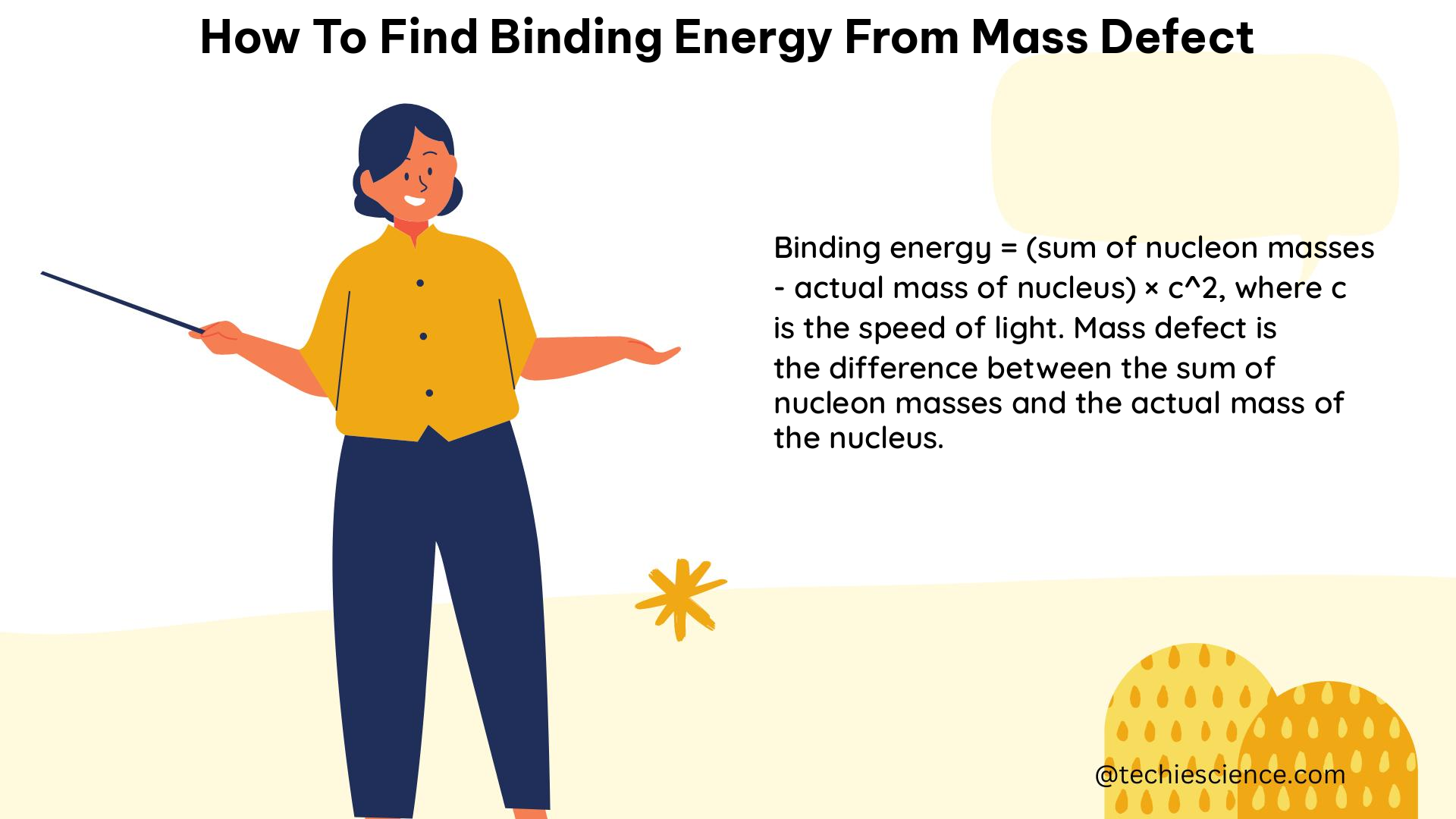
The mass defect can be converted into binding energy using Einstein’s mass-energy equivalence formula:

E = m × c^2

Where:
– E is the binding energy
– m is the mass defect
– c is the speed of light in a vacuum (approximately 3 × 10^8 m/s)

Continuing the example of the 16O nucleus, we can calculate the binding energy as follows:

Binding Energy = 0.14142 u × (931.5 MeV/u)
Binding Energy = 131.7 MeV

This binding energy represents the energy required to split the 16O nucleus into its individual protons and neutrons. It also indicates the strength of the nuclear force that holds the nucleons together in the nucleus.

Factors Affecting Binding Energy

The binding energy of a nucleus is influenced by several factors, including:

1. Nuclear Stability: Nuclei with a higher binding energy are more stable and less likely to undergo radioactive decay.
2. Nuclear Shell Structure: The binding energy of a nucleus is affected by the arrangement of protons and neutrons in the nuclear shell structure.
3. Neutron-to-Proton Ratio: The ratio of neutrons to protons in a nucleus can affect its binding energy, with the most stable nuclei having a specific neutron-to-proton ratio.
4. Nuclear Forces: The strong nuclear force, which is responsible for holding the nucleons together, is the primary factor determining the binding energy of a nucleus.

Calculating Binding Energy for Different Nuclei

To calculate the binding energy of a nucleus, you can follow these steps:

1. Determine the number of protons (Z) and neutrons (N) in the nucleus.
2. Calculate the theoretical mass of the nucleus by adding the masses of the constituent protons and neutrons.
3. Obtain the actual mass of the nucleus from experimental data or reference tables.
4. Calculate the mass defect using the formula: Mass Defect = (Z × m_p) + (N × m_n) – m_nucleus
5. Convert the mass defect to binding energy using the formula: Binding Energy = Mass Defect × c^2

Here are some examples of binding energy calculations for different nuclei:

Nucleus	Z	N	Theoretical Mass (u)	Actual Mass (u)	Mass Defect (u)	Binding Energy (MeV)
Hydrogen-1 (1H)	1	0	1.007825	1.007825	0	0
Helium-4 (4He)	2	2	4.032200	4.002603	0.029597	28.296
Carbon-12 (12C)	6	6	12.068654	12.000000	0.068654	92.163
Uranium-235 (235U)	92	143	235.043930	235.043930	0.203835	1802.295

As you can see, the binding energy increases with the complexity of the nucleus, reflecting the strong nuclear force that holds the nucleons together.

Applications of Binding Energy

The concept of binding energy has several important applications in nuclear physics and nuclear technology, including:

1. Nuclear Stability: Binding energy is a key indicator of nuclear stability, with more stable nuclei having higher binding energies.
2. Nuclear Reactions: The energy released or absorbed during nuclear reactions is directly related to the difference in binding energies between the reactants and products.
3. Nuclear Fission and Fusion: The energy released in nuclear fission and fusion reactions is a result of the change in binding energy between the initial and final nuclei.
4. Nuclear Weapons: The energy released in nuclear weapons is a consequence of the change in binding energy during the fission or fusion process.
5. Nuclear Power Generation: The energy released in nuclear power plants is a result of the controlled fission of heavy nuclei, such as Uranium or Plutonium.

Conclusion

Understanding the concept of binding energy and its relationship to mass defect is crucial in the field of nuclear physics. By mastering the techniques for calculating binding energy from mass defect, you can gain valuable insights into the stability and behavior of nuclei, as well as their applications in various areas of science and technology.

References:

1. Krane, Kenneth S. “Introductory Nuclear Physics.” John Wiley & Sons, 1988.
2. Serway, Raymond A., and John W. Jewett. “Physics for Scientists and Engineers.” Cengage Learning, 2018.
3. Knoll, Glenn F. “Radiation Detection and Measurement.” John Wiley & Sons, 2010.
4. Lilley, John. “Nuclear Physics: Principles and Applications.” John Wiley & Sons, 2001.
5. Meyerhof, Walter E. “Elements of Nuclear Physics.” McGraw-Hill, 1967.