In the field of physics and mechanics, understanding rotational motion is essential. One important concept in rotational motion is angular acceleration, which relates to the rate of change of angular velocity. In this blog post, we will explore how to find angular acceleration from angular velocity, step by step. We will also cover special cases and related concepts, providing clear explanations and examples along the way.
How to Calculate Angular Acceleration from Angular Velocity

The Mathematical Formula
The formula to calculate angular acceleration ![]() ) from angular velocity
) from angular velocity ![]() ) is given by:
) is given by:
![]()
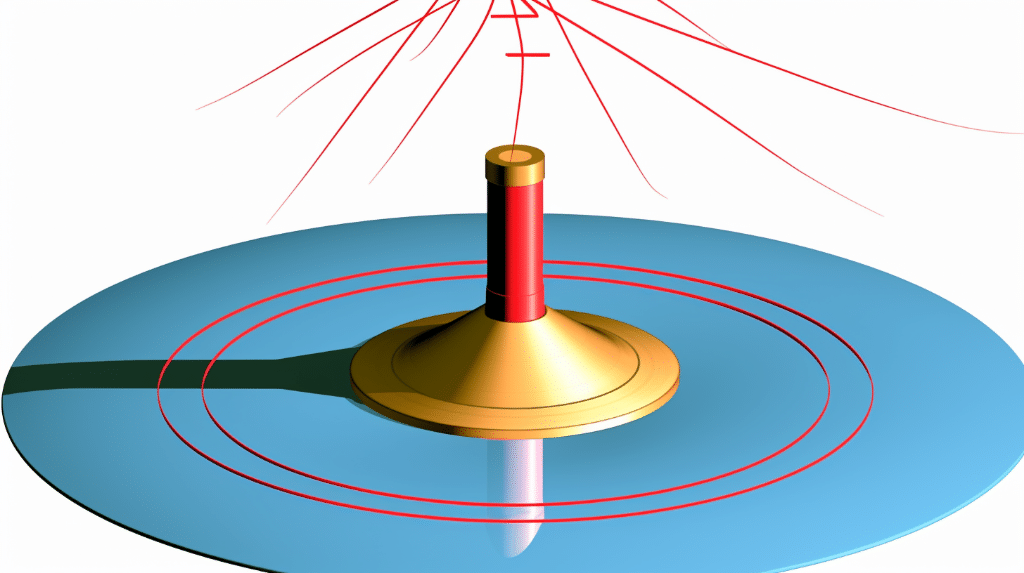
Here, ![]() represents the change in angular velocity, and
represents the change in angular velocity, and ![]() represents the change in time.
represents the change in time.
Step-by-Step Process
To find the angular acceleration from angular velocity, follow these steps:
- Identify the initial angular velocity
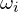 ) and the final angular velocity
) and the final angular velocity 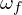 ).
). - Determine the time interval
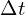 ) during which the change in angular velocity occurs.
) during which the change in angular velocity occurs. - Calculate the change in angular velocity
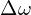 ) by subtracting the initial angular velocity from the final angular velocity:
) by subtracting the initial angular velocity from the final angular velocity: 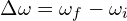 .
. - Divide the change in angular velocity by the change in time to obtain the angular acceleration:
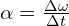 .
.
Worked out Example
Let’s work through an example to better understand how to find angular acceleration from angular velocity.
Example: A wheel starts with an initial angular velocity of 2 rad/s and accelerates uniformly to a final angular velocity of 8 rad/s over a time interval of 4 seconds. Calculate the angular acceleration.
Solution:
Given:
Initial angular velocity ![]() ) = 2 rad/s
) = 2 rad/s
Final angular velocity ![]() ) = 8 rad/s
) = 8 rad/s
Time interval ![]() ) = 4 s
) = 4 s
To find the angular acceleration ![]() ), we can use the formula:
), we can use the formula: ![]() .
.
First, calculate the change in angular velocity ![]() ):
):![]() .
.
Next, divide the change in angular velocity by the change in time:![]() .
.
Therefore, the angular acceleration of the wheel is ![]() .
.
Special Cases in Finding Angular Acceleration
How to Find Angular Acceleration without Time
In some cases, the time interval ![]() ) may not be given. However, it is still possible to find the angular acceleration using other known quantities.
) may not be given. However, it is still possible to find the angular acceleration using other known quantities.
If the initial angular velocity ![]() ), final angular velocity
), final angular velocity ![]() ), and the change in angular displacement
), and the change in angular displacement ![]() ) are known, the angular acceleration can be found using the following formula:
) are known, the angular acceleration can be found using the following formula:
![]()
Where ![]() represents the change in angular displacement.
represents the change in angular displacement.
How to Find Angular Acceleration from Angular Velocity and Radius
In situations where the angular velocity ![]() ) and radius
) and radius ![]() ) are known instead of time, the angular acceleration can be determined using the following formula:
) are known instead of time, the angular acceleration can be determined using the following formula:
![]()
Where ![]() represents the radius.
represents the radius.
How to Find Angular Acceleration from Angular Velocity and Time
If the angular velocity ![]() ) and tangential acceleration
) and tangential acceleration ![]() ) are given, the angular acceleration can be calculated using the formula:
) are given, the angular acceleration can be calculated using the formula:
![]()
Where ![]() is the radius.
is the radius.
Related Concepts
How to Find Tangential Acceleration from Angular Velocity
To find the tangential acceleration ![]() ) from angular velocity
) from angular velocity ![]() ) and radius
) and radius ![]() ), you can use the formula:
), you can use the formula:
![]()
This formula relates the linear velocity ![]() ) to the angular velocity
) to the angular velocity ![]() ) and radius
) and radius ![]() ), as tangential acceleration is the rate of change of linear velocity.
), as tangential acceleration is the rate of change of linear velocity.
How to Find Linear Acceleration from Angular Velocity
Linear acceleration ![]() ) can be determined from angular velocity
) can be determined from angular velocity ![]() ) and radius
) and radius ![]() ) using the formula:
) using the formula:
![]()
Where ![]() represents the angular acceleration.
represents the angular acceleration.
How to Calculate Centripetal Acceleration from Angular Velocity
Centripetal acceleration ![]() ) can be calculated using the formula:
) can be calculated using the formula:
![]()
Here, ![]() represents the linear velocity and
represents the linear velocity and ![]() is the radius.
is the radius.
Understanding how to find angular acceleration from angular velocity is crucial for analyzing rotational motion. By following the steps outlined in this blog post, you can calculate angular acceleration accurately. Remember to consider special cases and related concepts to gain a comprehensive understanding of this topic.
How can you find the constant angular acceleration from the given angular velocity in a motion?
To find the constant angular acceleration from the given angular velocity, you can follow the steps mentioned in the article Finding constant angular acceleration in motion. First, determine the final angular velocity and initial angular velocity. Then, calculate the change in angular velocity and the change in time. Finally, divide the change in angular velocity by the change in time to obtain the constant angular acceleration. This method helps in quantifying the change in angular velocity over a specific period of time, enabling a deeper understanding of the motion’s behavior.
Numerical Problems on how to find angular acceleration from angular velocity
Problem 1:
An object is rotating with an angular velocity of 4 rad/s. It accelerates uniformly at a rate of 2 rad/s^2 for a time of 5 seconds. Find the final angular velocity of the object.
Solution:
Given:
Initial angular velocity, ![]() rad/s
rad/s
Angular acceleration, ![]() rad/s
rad/s![]()
Time, ![]() s
s
The final angular velocity can be calculated using the formula:![]()
Substituting the given values, we have:![]()
Therefore, the final angular velocity of the object is 14 rad/s.
Problem 2:
A wheel starts from rest and rotates with an angular acceleration of 3 rad/s^2. If it rotates for a time of 10 seconds, find the final angular velocity of the wheel.
Solution:
Given:
Initial angular velocity, ![]() rad/s (as the wheel starts from rest)
rad/s (as the wheel starts from rest)
Angular acceleration, ![]() rad/s
rad/s![]()
Time, ![]() s
s
The final angular velocity can be calculated using the formula:![]()
Substituting the given values, we have:![]()
Therefore, the final angular velocity of the wheel is 30 rad/s.
Problem 3:
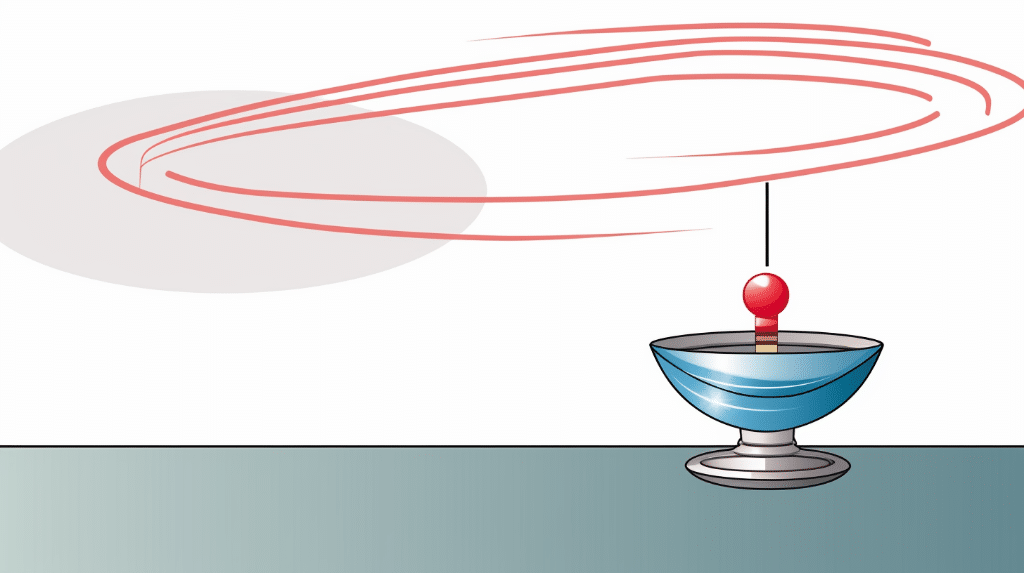
A fan blade initially rotates with an angular velocity of 8 rad/s. It decelerates uniformly at a rate of 4 rad/s^2 for a time of 2 seconds. Find the final angular velocity of the fan blade.
Solution:
Given:
Initial angular velocity, ![]() rad/s
rad/s
Angular acceleration, ![]() rad/s
rad/s![]() (negative sign indicates deceleration)
(negative sign indicates deceleration)
Time, ![]() s
s
The final angular velocity can be calculated using the formula:![]()
Substituting the given values, we have:![]()
Therefore, the final angular velocity of the fan blade is 0 rad/s.
Also Read:
- Zero velocity graph
- How to find the kinetic energy and velocity
- How to find velocity of a wave
- Drag coefficient and velocity
- How to find velocity ratio
- Escape velocity of earth
- Is angular velocity a vector
- Negative constant velocity graph
- How to determine velocity in radio astronomy
- How to find velocity at impact
Hi, I’m Akshita Mapari. I have done M.Sc. in Physics. I have worked on projects like Numerical modeling of winds and waves during cyclone, Physics of toys and mechanized thrill machines in amusement park based on Classical Mechanics. I have pursued a course on Arduino and have accomplished some mini projects on Arduino UNO. I always like to explore new zones in the field of science. I personally believe that learning is more enthusiastic when learnt with creativity. Apart from this, I like to read, travel, strumming on guitar, identifying rocks and strata, photography and playing chess.