How to Find Activation Energy: A Comprehensive Guide

by

The activation energy (Ea) of a chemical reaction is a crucial parameter that determines the rate at which the reaction occurs. It represents the minimum amount of energy required for the reactants to overcome the energy barrier and form the products. Understanding how to accurately determine the activation energy is essential for chemists, physicists, and engineers working in various fields, such as catalysis, reaction kinetics, and material science. In this comprehensive guide, we will delve into the step-by-step process of finding the activation energy using the Arrhenius equation and provide detailed examples to help you master this important concept.

The Arrhenius Equation and Activation Energy

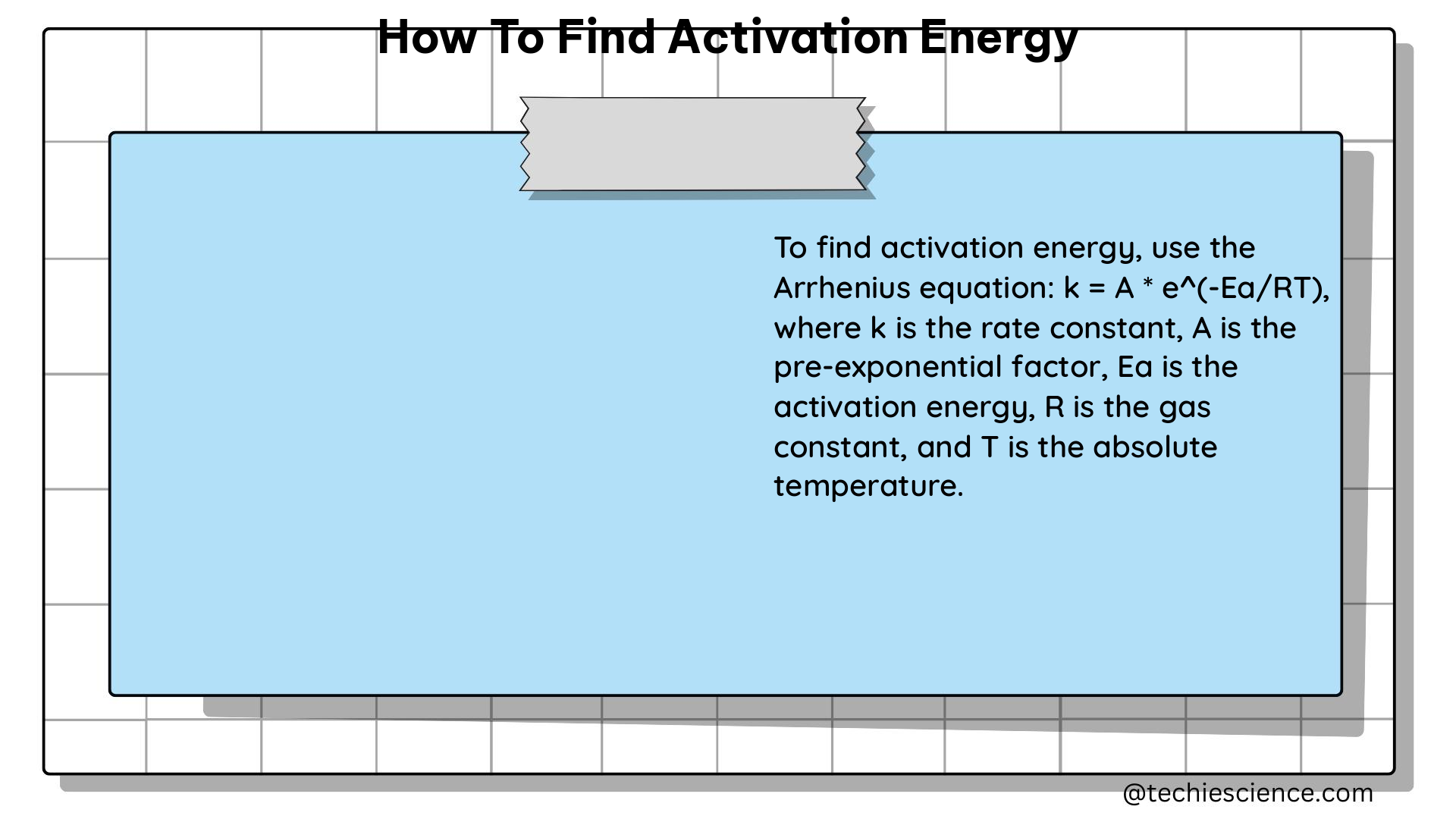
The relationship between the rate constant (k) of a chemical reaction and the activation energy (Ea) is described by the Arrhenius equation, which is given by:

k = A * e^(-Ea/(RT))

where:
– k is the rate constant of the reaction
– A is the pre-exponential factor, which represents the frequency of collisions between reactant molecules
– Ea is the activation energy of the reaction
– R is the universal gas constant (8.314 J/mol·K)
– T is the absolute temperature in Kelvin (K)

The Arrhenius equation demonstrates that the rate constant of a reaction increases exponentially as the activation energy decreases or the temperature increases. By rearranging the equation, we can isolate the activation energy and determine its value.

Determining Activation Energy Using the Arrhenius Equation

how to find activation energy

To find the activation energy of a reaction, you can follow these steps:

  1. Collect Experimental Data: Obtain the rate constant (k) of the reaction at different temperatures (T). This data can be obtained through experimental measurements or from literature sources.

  2. Calculate ln(k): For each temperature, calculate the natural logarithm of the rate constant, ln(k).

  3. Plot ln(k) vs. 1/T: Create a plot of the natural logarithm of the rate constant (ln(k)) on the y-axis and the reciprocal of the absolute temperature (1/T) on the x-axis. This plot is known as the Arrhenius plot.

  4. Determine the Slope: The slope of the Arrhenius plot will be equal to -Ea/R. This can be determined using linear regression or by visually inspecting the plot.

  5. Calculate the Activation Energy: Once you have the slope, you can calculate the activation energy (Ea) using the formula:

Ea = -slope * R

where R is the universal gas constant (8.314 J/mol·K).

Let’s illustrate this process with an example.

Example: Determining the Activation Energy of a Reaction

Suppose we have the following experimental data for the rate constant (k) of a reaction at different temperatures:

Temperature (K) Rate Constant (s^-1)
298 1.74 × 10^-5
308 6.61 × 10^-5
318 2.51 × 10^-4
328 7.59 × 10^-4
338 2.40 × 10^-3

To find the activation energy, we can follow the steps outlined earlier:

  1. Calculate ln(k): We can calculate the natural logarithm of the rate constant (ln(k)) for each temperature:
Temperature (K) Rate Constant (s^-1) ln(k)
298 1.74 × 10^-5 -11.2533
308 6.61 × 10^-5 -8.6808
318 2.51 × 10^-4 -5.5252
328 7.59 × 10^-4 -2.9957
338 2.40 × 10^-3 1.1774
  1. Plot ln(k) vs. 1/T: Create a plot of the natural logarithm of the rate constant (ln(k)) on the y-axis and the reciprocal of the absolute temperature (1/T) on the x-axis:

Arrhenius Plot

  1. Determine the Slope: The slope of the Arrhenius plot is -Ea/R. Using linear regression or visual inspection, we can determine the slope to be approximately -8 × 10^-5.

  2. Calculate the Activation Energy: Substituting the slope and the value of the universal gas constant (R = 8.314 J/mol·K) into the formula, we can calculate the activation energy:

Ea = -slope * R
Ea = -(-8 × 10^-5) * 8.314 J/mol·K
Ea = 0.0665 J/mol

Therefore, the activation energy of the reaction is approximately 66.5 J/mol.

Additional Considerations and Techniques

  1. Temperature Range: It is important to choose a suitable temperature range for the Arrhenius plot. The temperature range should be wide enough to provide a clear linear relationship between ln(k) and 1/T, but not too wide to avoid significant changes in the reaction mechanism or other factors that may affect the rate constant.

  2. Experimental Uncertainty: When collecting experimental data, it is crucial to consider the uncertainty in the rate constant measurements. This uncertainty can be incorporated into the Arrhenius plot and the subsequent calculation of the activation energy.

  3. Alternative Techniques: In addition to the Arrhenius plot method, there are other techniques for determining the activation energy, such as the initial rate method and the half-life method. These methods may be more suitable for specific types of reactions or when the rate constant data is limited.

  4. Theoretical Calculations: In some cases, the activation energy can be estimated using theoretical methods, such as quantum mechanical calculations or molecular dynamics simulations. These approaches can provide valuable insights into the reaction mechanism and the factors that influence the activation energy.

  5. Catalytic Effects: The presence of a catalyst can significantly alter the activation energy of a reaction. By studying the changes in activation energy with and without a catalyst, you can gain insights into the catalytic mechanism and the role of the catalyst in lowering the energy barrier.

Conclusion

Determining the activation energy of a chemical reaction is a crucial step in understanding the kinetics and mechanisms of the process. By using the Arrhenius equation and the Arrhenius plot method, you can accurately calculate the activation energy from experimental rate constant data. This knowledge is essential for optimizing reaction conditions, designing efficient catalysts, and predicting the behavior of chemical systems. With the detailed steps and examples provided in this guide, you should now have a comprehensive understanding of how to find the activation energy of a reaction.

References