To compute acceleration ![]() using initial velocity
using initial velocity ![]() , final velocity
, final velocity ![]() , and distance
, and distance ![]() , apply the formula
, apply the formula ![]() . This equation originates from the kinematic relation
. This equation originates from the kinematic relation ![]() , assuming linear motion and constant acceleration. Acceleration, being a vector, encompasses both magnitude and direction; this formula calculates the magnitude. In cases of non-uniform acceleration, integration of the velocity function
, assuming linear motion and constant acceleration. Acceleration, being a vector, encompasses both magnitude and direction; this formula calculates the magnitude. In cases of non-uniform acceleration, integration of the velocity function ![]() is necessary. Consistent unit usage is crucial:
is necessary. Consistent unit usage is crucial: ![]() and
and ![]() in meters per second (
in meters per second (![]() ),
), ![]() in meters (
in meters (![]() ), yielding
), yielding ![]() in meters per second squared (
in meters per second squared (![]() ).
).
How to find acceleration with velocity and distance without time
To find acceleration without time, use ![]() , where
, where ![]() is acceleration,
is acceleration, ![]() final velocity,
final velocity, ![]() initial velocity,
initial velocity, ![]() distance. This derives from
distance. This derives from ![]() , a kinematic equation for constant acceleration, ensuring precise calculation when time data is unavailable.
, a kinematic equation for constant acceleration, ensuring precise calculation when time data is unavailable.
How to find acceleration with distance time and initial velocity
To find acceleration with distance, time, and initial velocity, use ![]() . Here,
. Here, ![]() is acceleration,
is acceleration, ![]() distance,
distance, ![]() initial velocity,
initial velocity, ![]() time. This formula accurately calculates acceleration, particularly in linear motion with uniform acceleration, providing a precise assessment in scenarios where final velocity is unknown.
time. This formula accurately calculates acceleration, particularly in linear motion with uniform acceleration, providing a precise assessment in scenarios where final velocity is unknown.
Acceleration: A Quantitative Overview
Formula Derivation
Acceleration, denoted as a, is defined as the rate of change of velocity (v) over time (t). In situations where only velocity and distance (s) are known, the equation used is:
![]()
Here, v is the final velocity, u is the initial velocity, and s is the distance covered.
Underlying Physics
This formula is derived from kinematic equations under constant acceleration, integrating the principle of work-energy where the kinetic energy difference equates to the work done against the force causing acceleration.
Advanced Calculation Techniques
Case Study: Variable Acceleration
In cases of variable acceleration, calculus is employed. The velocity function v(t) is integrated over time to find distance, and its derivative gives acceleration:
![]()
![]()
![]()
Real-World Example: A Car’s Acceleration
For instance, a car accelerating from 0 to 60 km/h over 100 meters. Using our formula:
![]()
![]()
Practical Application: Experimental Approach
Setup and Measurement Techniques
- Equipment: Motion sensor, track, and data analysis software.
- Procedure: Release an object on the track, recording its velocity.
- Data Analysis: Plot velocity vs. time, calculate acceleration.
Experiment: Verifying Theoretical Values
Conduct experiments, e.g., an object sliding down an inclined plane, measure the distance and final velocity, then calculate and compare the theoretical and experimental acceleration.
Challenges in Accurate Determination
Factors Affecting Accuracy
- Air Resistance: Affects results, especially at high velocities.
- Measurement Errors: Inaccurate distance or velocity measurements lead to erroneous acceleration calculations.
- Friction: Introduces opposing force, affecting acceleration.
The Constant Acceleration Equations OR The Kinematics Formulas:
Kinematics formulas that are only relevant when an object or body moves with a constant acceleration within a given time interval are known as constant acceleration equations. When it comes to constant acceleration, the acceleration caused by gravity is the best real world example. It is commonly symbolized by the letter ‘g,’ whose value on the earth’s surface is 9.8 m/s2.
The kinematic formulas, often known as constant acceleration equations, are a series of formulas that link the five kinematic variables given below.
- a Constant Acceleration
- v0 Initial Velocity
- v Finale Velocity
- t Time Interval
- ð›¥x Distance traveled by an object in one direction
Suppose an object or body is under constant acceleration, and three of these five kinematic variables (a, v, v0, t, x) are known. In that case, we can use the kinematic equations given below to solve one of the unknown variables.
1. v = v0 + at
2. ð›¥x = v0t + (1/2)at2
3. v2 = v02 + 2að›¥x
How do you choose and apply a constant acceleration formula?
In kinematics, we have three equations of constant acceleration. Out of five kinematic variables, four are present in each equation.
We must select the constant acceleration equation that incorporates both the unknown variable we are looking for and three of the known kinematic variables. By introducing known variable values into the equation, we can find the unknown variable that is only unknown in the equation.
Consider the case of dragging a box that was initially steady. After 5 seconds, its velocity had increased to 10 m/s. Consider a constant acceleration for 5 seconds. Because we have v0, v, and t, we can find the value of the unknown constant acceleration by applying the equation v = v0 + at.
Let us see some problems of finding acceleration using velocity and distance.
But our primary concern for this article is to figure out how to calculate acceleration using velocity and distance. So, let us now talk about how to find acceleration with velocity and distance.
How to find acceleration with velocity and distance?
The constant acceleration equation is the one that is used in kinematics to find acceleration using velocity and distance.
If we have an initial velocity, a final velocity, and a distance but don’t know the time interval, we can apply the constant acceleration equation v2 = v02 + 2að›¥x to get the acceleration.
We have three known quantities and one unknown quantity in the above equation. We can calculate the constant acceleration by placing all three known values in an equation and making acceleration the subject of the equation. As a result, acceleration is determined by rearranging the above equation and given by:

We can find acceleration with velocity and distance using the equation above. Keep in mind that the constant acceleration equations only work if the acceleration is constant (as the name suggests) and in one direction. When dealing with two-dimensional or three-dimensional motion, things become more complicated. However, by applying the above equations for constant acceleration, one may build equations of motion for each direction separately. These simple equations aren’t used when acceleration is changing; instead, complex calculus is used.
Problem: A bike constantly accelerates from rest to a speed of 10 m/s across a distance of 20 m. Determine the acceleration of the bike.
Given:
The initial velocity of the bike v0 = 0 m/s (As initially, the bike is at rest)
Finale velocity of the bike v = 10 m/s
Distance traveled by the bike ð›¥x = 20 m
To Find:
Constant acceleration of the bike a = ?
Solution:
Putting the values in the above equation:
∴ a = 2.5 m/s2
As a result, the bike’s acceleration is 2.5 m/s2.
Problem: From a height of 1.40 meters, a feather is dropped onto the moon. If the feather’s velocity is 2.135 m/s, then determine the acceleration of gravity on the moon.
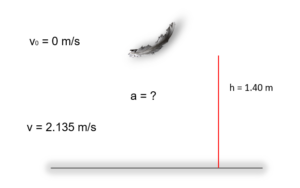
Image Credits: Wikipedia
Given:
Initial velocity of the feather v0 = 0 m/s (As in free falling initial velocity is zero)
Finale velocity of the feather v = 2.135 m/s
Distance traveled by the feather ð›¥x = 1.40 m
To Find:
Acceleration due to gravity on the surface of the moon a = ?
Solution:
Putting the values in the above equation:
∴ a = 1.625 m/s2
Problem: At a speed of 12 m/s, a racing boat crosses the finish line and continues straight ahead. It came to a halt 18 meters from the finish line. What is the magnitude of the acceleration of the racing boat if it instantly decelerates till it comes to a stop?
Given:
Initial velocity of the racing boat v0 = 12 m/s
Explore the advanced science and research posts to learn more.
Finale velocity of the racing boat v = 0 m/s (As it comes to a stop)
Distance traveled by the racing boat ð›¥x = 18 m
To find:
Constant acceleration of the racing boat a = ?
Solution:
Putting the values in the above equation:
∴ a = -4 m/s2
The negative sign indicates that the racing boat’s acceleration decreases and its value is 4 m/s2.
We hope we have answered all of your questions on how to find acceleration with velocity and distance.
Explore the advanced science and research posts to learn more.
Also Read:
- Instantaneous velocity vs acceleration
- How to measure velocity of fluid in porous medium
- How to find radial acceleration without velocity
- How to find velocity in statistical mechanics
- Velocity after collision formula
- How to find velocity in aerodynamics
- Instantaneous velocity vs velocity
- How to find angular velocity in rotational dynamics
- Velocity formula
- How to determine velocity in geophysics

I am Alpa Rajai, Completed my Masters in science with specialization in Physics. I am very enthusiastic about Writing about my understanding towards Advanced science. I assure that my words and methods will help readers to understand their doubts and clear what they are looking for. Apart from Physics, I am a trained Kathak Dancer and also I write my feeling in the form of poetry sometimes. I keep on updating myself in Physics and whatever I understand I simplify the same and keep it straight to the point so that it deliver clearly to the readers.