Summary
Determining the acceleration of an object with mass and air resistance involves considering the net force acting on the object, which is the sum of the weight (W) and the aerodynamic drag (D) due to air resistance. By using the formula F = W + D to calculate the net force and then applying the formula a = F/m to find the acceleration, you can accurately determine the object’s acceleration, taking into account the effects of both mass and air resistance.
Understanding the Fundamentals
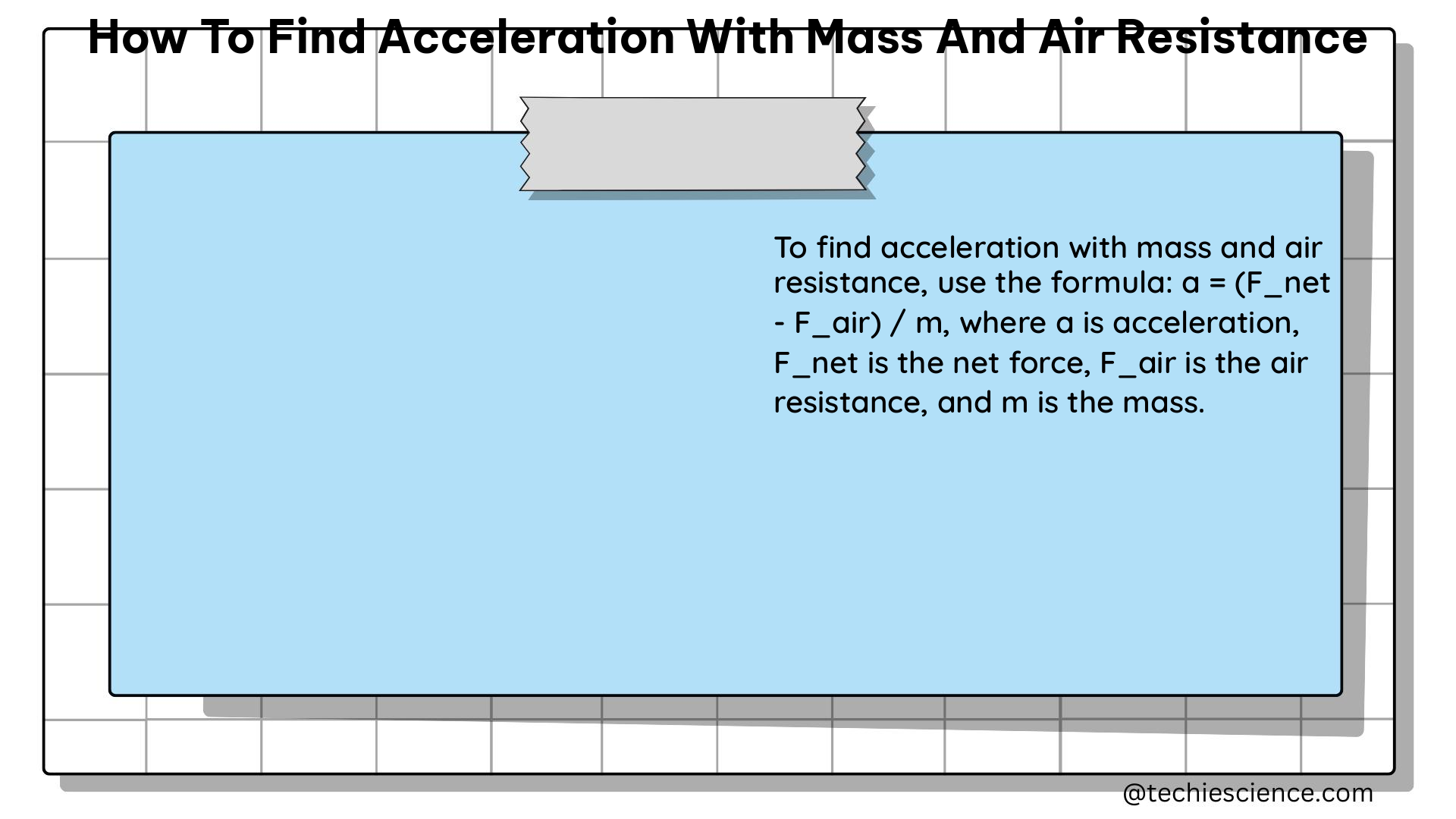
To find the acceleration of an object with mass and air resistance, we need to consider the net force acting on the object. The net force (F) is the sum of the weight (W) and the aerodynamic drag (D) due to air resistance.
The formula for the net force is:
F = W + D
Where:
– W = m × g (m is the mass of the object, and g is the acceleration due to gravity)
– D = 0.5 × Cd × ρ × v^2 × A (Cd is the drag coefficient, ρ is the air density, v is the velocity of the object, and A is the cross-sectional area of the object)
Once we have the net force, we can use the formula:
a = F / m
to calculate the acceleration of the object.
Calculating the Weight (W)
The weight of the object is calculated using the formula:
W = m × g
Where:
– m is the mass of the object
– g is the acceleration due to gravity (9.81 m/s^2)
For example, if the mass of the object is 0.006161125 kg, the weight would be:
W = 0.006161125 kg × 9.81 m/s^2 = 0.06042 N
Calculating the Aerodynamic Drag (D)
The aerodynamic drag (D) is calculated using the formula:
D = 0.5 × Cd × ρ × v^2 × A
Where:
– Cd is the drag coefficient (dimensionless)
– ρ is the air density (1.1839 kg/m^3 at 20°C and 1 atm)
– v is the velocity of the object
– A is the cross-sectional area of the object
For example, if the object is a tennis ball with a radius of 6.86 cm, the cross-sectional area would be:
A = π × r^2 = π × (0.0686 m)^2 = 0.015 m^2
Assuming the drag coefficient (Cd) for a sphere is 0.47 and the velocity (v) is 4.756 m/s, the aerodynamic drag would be:
D = 0.5 × 0.47 × 1.1839 kg/m^3 × (4.756 m/s)^2 × 0.015 m^2 = 0.94396922 N
Calculating the Net Force (F)
With the weight (W) and the aerodynamic drag (D) calculated, we can now find the net force (F) using the formula:
F = W + D
For the example values:
F = 0.06042 N + 0.94396922 N = 1.00436922 N
Calculating the Acceleration (a)
Finally, we can use the net force (F) and the mass (m) to calculate the acceleration (a) using the formula:
a = F / m
For the example values:
a = 1.00436922 N / 0.006161125 kg = 163.02 m/s^2
This value is much higher than the acceleration due to gravity (9.81 m/s^2), indicating that the object is accelerating downwards due to the combined effect of its weight and the aerodynamic drag.
Additional Considerations
- It’s important to consider the direction of the forces when calculating the net force. The weight of the object is downwards, while the aerodynamic drag is upwards.
- The drag coefficient (Cd) can vary depending on the shape and orientation of the object. For example, a sphere has a Cd of around 0.47, while a streamlined object may have a much lower Cd.
- The air density (ρ) can also vary depending on factors such as temperature and altitude.
- The velocity (v) of the object can change over time, so it’s important to use the appropriate value for the given scenario.
Practical Examples and Numerical Problems
- Example 1: A skydiver with a mass of 80 kg jumps from an airplane. The skydiver’s drag coefficient is 0.7, and the cross-sectional area is 0.5 m^2. Assume the air density is 1.225 kg/m^3 and the initial velocity is 0 m/s. Calculate the acceleration of the skydiver during the free fall.
Given:
– Mass (m) = 80 kg
– Drag coefficient (Cd) = 0.7
– Cross-sectional area (A) = 0.5 m^2
– Air density (ρ) = 1.225 kg/m^3
– Initial velocity (v) = 0 m/s
Step 1: Calculate the weight (W)
W = m × g = 80 kg × 9.81 m/s^2 = 784.8 N
Step 2: Calculate the aerodynamic drag (D)
D = 0.5 × Cd × ρ × v^2 × A = 0.5 × 0.7 × 1.225 kg/m^3 × (0 m/s)^2 × 0.5 m^2 = 0 N
Step 3: Calculate the net force (F)
F = W + D = 784.8 N + 0 N = 784.8 N
Step 4: Calculate the acceleration (a)
a = F / m = 784.8 N / 80 kg = 9.81 m/s^2
The acceleration of the skydiver during the free fall is 9.81 m/s^2, which is the same as the acceleration due to gravity.
- Example 2: A baseball with a mass of 0.145 kg is hit with an initial velocity of 40 m/s. The baseball has a diameter of 7.3 cm, and the air density is 1.225 kg/m^3. Assume the drag coefficient (Cd) for a baseball is 0.35. Calculate the acceleration of the baseball after 1 second.
Given:
– Mass (m) = 0.145 kg
– Initial velocity (v) = 40 m/s
– Diameter = 7.3 cm = 0.073 m
– Air density (ρ) = 1.225 kg/m^3
– Drag coefficient (Cd) = 0.35
Step 1: Calculate the cross-sectional area (A)
A = π × (d/2)^2 = π × (0.073 m/2)^2 = 0.0042 m^2
Step 2: Calculate the weight (W)
W = m × g = 0.145 kg × 9.81 m/s^2 = 1.42 N
Step 3: Calculate the aerodynamic drag (D)
D = 0.5 × Cd × ρ × v^2 × A = 0.5 × 0.35 × 1.225 kg/m^3 × (40 m/s)^2 × 0.0042 m^2 = 10.5 N
Step 4: Calculate the net force (F)
F = W + D = 1.42 N + 10.5 N = 11.92 N
Step 5: Calculate the acceleration (a)
a = F / m = 11.92 N / 0.145 kg = 82.2 m/s^2
The acceleration of the baseball after 1 second is 82.2 m/s^2.
These examples demonstrate how to apply the formulas and principles discussed earlier to calculate the acceleration of objects with mass and air resistance. Remember to consider the direction of the forces and use the appropriate values for the given scenario.
Conclusion
Determining the acceleration of an object with mass and air resistance involves a step-by-step process of calculating the net force acting on the object and then using that net force to find the acceleration. By understanding the formulas and principles involved, you can accurately determine the acceleration of an object in various scenarios, taking into account the effects of both mass and air resistance.
References
- Acceleration with air resistance – Physics Stack Exchange
- Finding Acceleration – The Physics Classroom
- Calculating Horizontal Acceleration in Systems with Friction | Physics
- Calculating Acceleration from Force and Mass | CK-12 Foundation
- How can air resistance be calculated using mass and acceleration? – CK-12 Foundation

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.