Mastering Kinematic Equations: A Comprehensive Guide to Finding Acceleration

Kinematic equations are fundamental tools in physics for analyzing the motion of objects. These equations allow us to determine the acceleration of an object given its initial and final velocities, positions, and the time elapsed. In this comprehensive guide, we will delve into the step-by-step process of using kinematic equations to find acceleration, providing detailed explanations, formulas, examples, and problem-solving strategies.

Steps to Find Acceleration Using Kinematic Equations

1. Identify the Object’s Starting Velocity and Position
2. Determine the initial velocity (v_i) and initial position (x_i) of the object.

3. These values represent the starting conditions of the motion.

4. Identify the Object’s Final Velocity and Position

5. Determine the final velocity (v_f) and final position (x_f) of the object.

6. These values represent the ending conditions of the motion.

7. Identify the Distance Traveled Between the Start and the End

8. Calculate the displacement (x_f – x_i) of the object, which is the distance traveled.

9. Identify the Time Difference Between the Start and the End

10. Determine the time (t) elapsed between the initial and final conditions.

11. Identify the Appropriate Kinematic Equation

12. Choose the kinematic equation that best fits the given information and the unknown quantity you need to solve for.

13. Plug in the Values and Solve for Acceleration

14. Substitute the known values into the selected kinematic equation and solve for the acceleration (a).

15. Check the Units for Acceleration

16. Ensure that the calculated acceleration is in the correct unit, which is meters per second squared (m/s^2).

Kinematic Equations

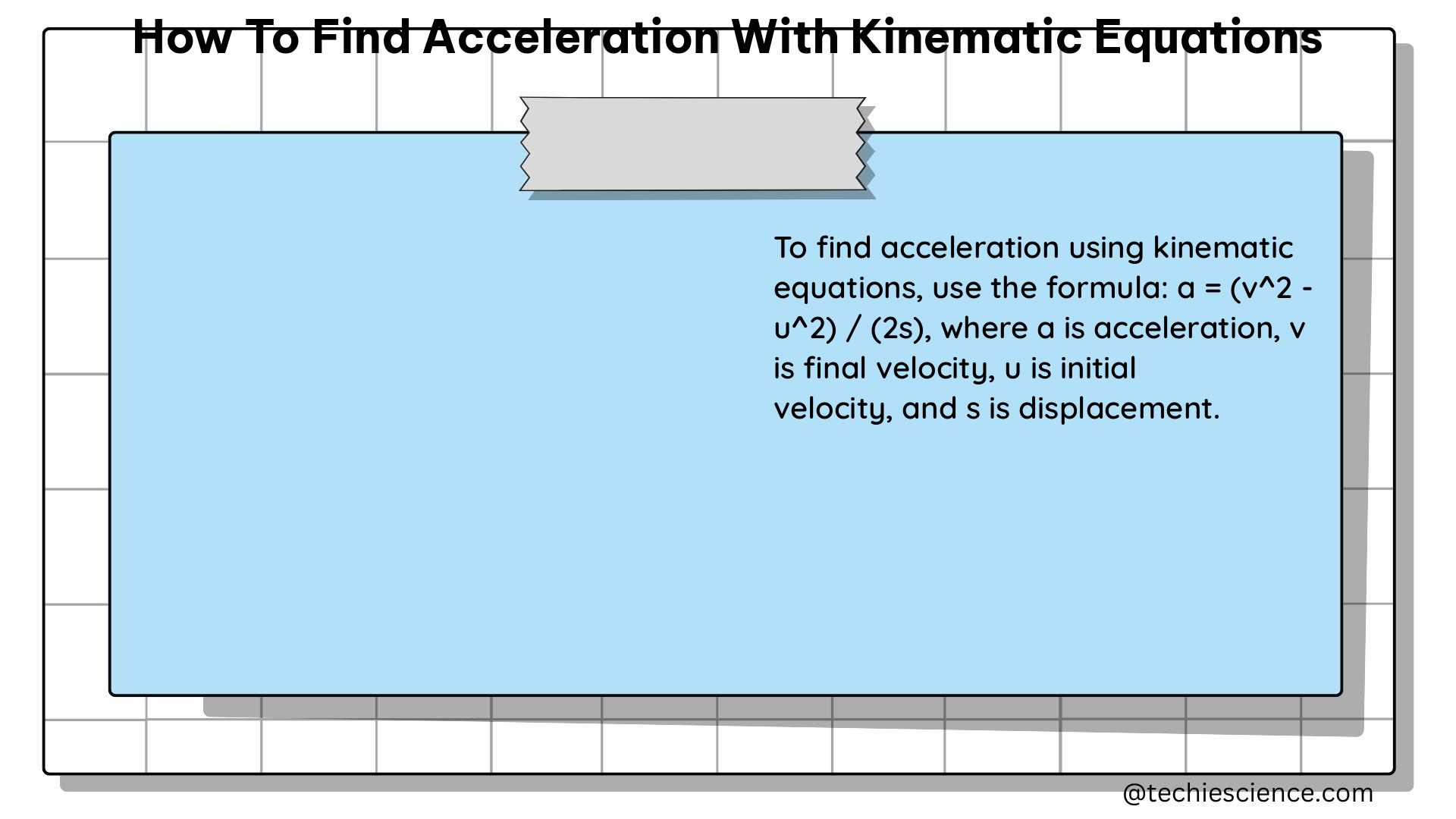
The four fundamental kinematic equations are:

1. Displacement Equation:
   [
   x_f – x_i = \frac{(v_f + v_i)t}{2}
   ]

2. Velocity Change Equation:
   [
   v_f – v_i = at
   ]

3. Velocity-Squared Equation:
   [
   v_f^2 = v_i^2 + 2a(x_f – x_i)
   ]

4. Position-Time Equation:
   [
   x_f = x_i + v_it + \frac{1}{2}at^2
   ]

These equations relate the object’s initial and final velocities, positions, and the time elapsed. By rearranging the equations, you can solve for the unknown variable, which in this case is the acceleration.

Example: Finding Acceleration of a Thrown Ball

Let’s consider the example of a ball thrown upward from the ground with an initial velocity of 5 m/s. The ball reaches a height of 10 meters before falling back to the ground.

Given:
– Initial velocity (v_i) = 5 m/s
– Initial position (x_i) = 0 m
– Final velocity (v_f) = 0 m/s (at the top of the ball’s flight)
– Final position (x_f) = 10 m
– Time (t) is unknown

Step 1: Identify the object’s starting velocity and position.
– v_i = 5 m/s
– x_i = 0 m

Step 2: Identify the object’s final velocity and position.
– v_f = 0 m/s (at the top of the ball’s flight)
– x_f = 10 m

Step 3: Identify the distance traveled between the start and the end.
– x_f – x_i = 10 m

Step 4: Identify the time difference between the start and the end.
– t is unknown

Step 5: Identify the appropriate kinematic equation.
– In this case, we can use the Velocity-Squared Equation: v_f^2 = v_i^2 + 2a(x_f – x_i)

Step 6: Plug in the values and solve for acceleration.
[
0^2 = 5^2 + 2a(10 – 0) \
0 = 25 + 20a \
a = -\frac{25}{20} = -1.25 m/s^2
]

Step 7: Check the units for acceleration.
– The calculated acceleration is -1.25 m/s^2, which is in the correct unit.

This example demonstrates how to use the Velocity-Squared Equation to find the acceleration of the ball. The negative value of acceleration indicates that the ball is experiencing downward acceleration due to gravity.

Advanced Techniques and Considerations

1. Hidden Quantities:
2. Be aware of quantities that might be given indirectly, such as displacement instead of initial and final positions.

3. Carefully analyze the problem statement to identify all the necessary information.

4. Direction:

5. Keep track of the direction of motion by using negative values for downward motion and positive values for upward motion.

6. This is crucial for correctly interpreting the sign of the acceleration.

7. Constant Acceleration:

8. The kinematic equations presented here assume constant acceleration throughout the motion.

9. If the acceleration is not constant, these equations may not be applicable, and you may need to use more advanced techniques.

10. Graphical Representations:

11. Plotting position-time, velocity-time, and acceleration-time graphs can provide valuable insights and help visualize the motion.

12. Analyzing these graphs can assist in identifying the appropriate kinematic equation to use.

13. Dimensional Analysis:

14. Carefully check the units of the given quantities and the calculated acceleration to ensure dimensional consistency.

15. This helps validate the correctness of your work and the physical meaning of the results.

16. Problem-Solving Strategies:

17. Develop a systematic approach to identify the known and unknown variables in the problem.

18. Practice solving a variety of kinematic problems to build your problem-solving skills.

19. Numerical Examples and Practice Problems:

20. Engage in solving numerous numerical examples and practice problems to reinforce your understanding of kinematic equations and their applications.
21. This will help you become proficient in finding acceleration using kinematic equations.

By mastering these techniques and considerations, you will be well-equipped to tackle a wide range of kinematic problems and confidently find the acceleration of objects using the provided kinematic equations.

References

1. Cambridge Coaching. (n.d.). How to Solve Kinematics Problems, Part 2. Retrieved from https://blog.cambridgecoaching.com/how-to-solve-kinematics-problems-part-ii/
2. Open Oregon. (n.d.). Quantitative Motion Analysis. Retrieved from https://openoregon.pressbooks.pub/bodyphysics/chapter/quantitative-motion-analysis/
3. The Physics Classroom. (n.d.). Kinematic Equations. Retrieved from https://www.physicsclassroom.com/class/1DKin/Lesson-6/Kinematic-Equations
4. College Vine. (2021). AP Physics 1 Kinematics Equations You Need to Know + Practice Problems. Retrieved from https://blog.collegevine.com/ap-physics-1-kinematics-equations-and-practice-problems/
5. Study.com. (2021). Using Kinematic Equations to Solve for an Unknown Acceleration. Retrieved from https://study.com/skill/learn/using-kinematic-equations-to-solve-for-an-unknown-acceleration-explanation.html