Calculating acceleration using height and time is a fundamental concept in physics, particularly in the study of one-dimensional motion. This comprehensive guide will provide you with a deep understanding of the underlying principles, equations, and practical applications to help you master this essential skill.
Understanding the Equation for Acceleration
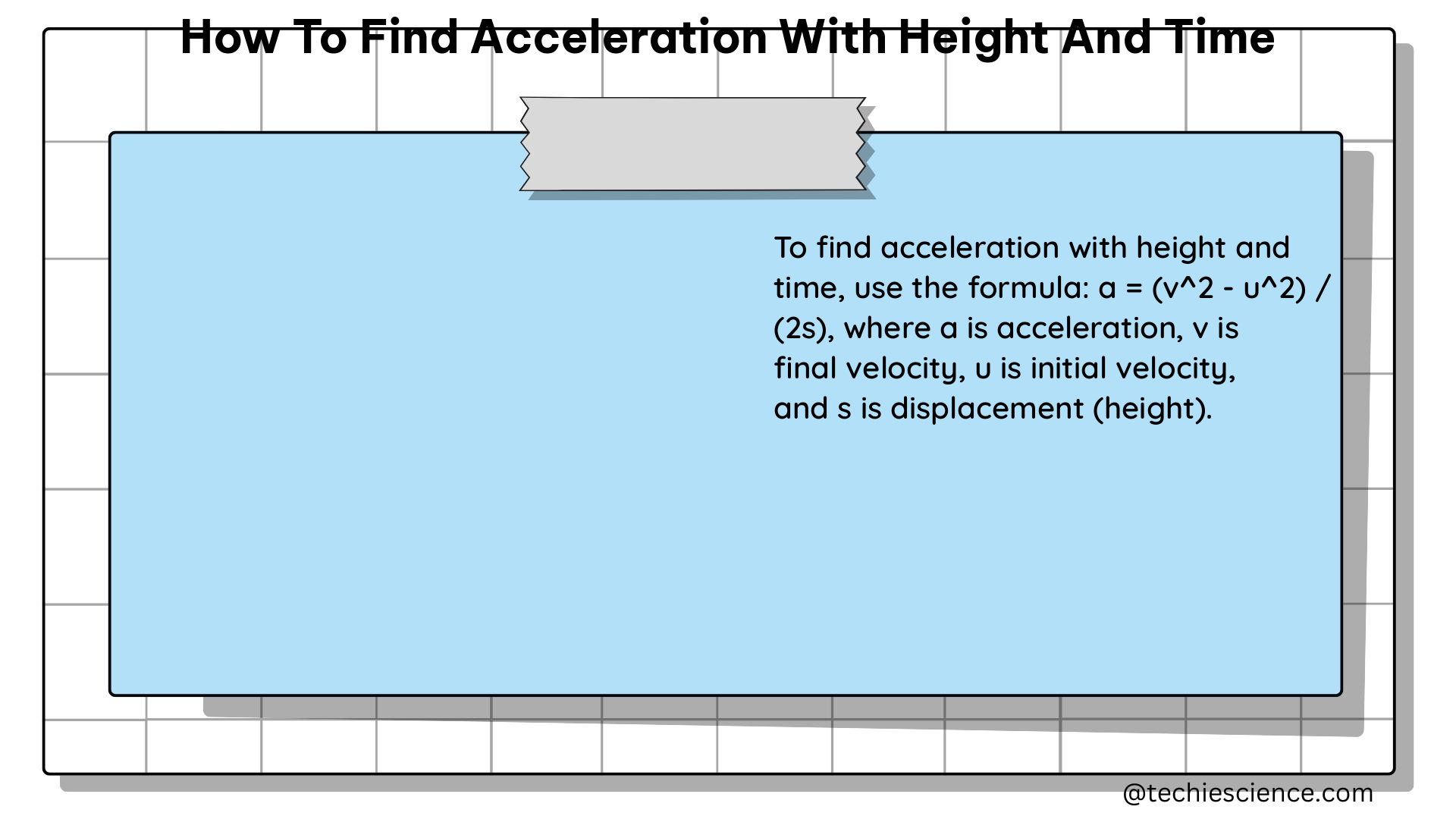
The equation to find acceleration with height and time is:
a = (√(2ghf) - √(2ghi)) / Δt
Where:
– a is the acceleration of the object
– g is the acceleration due to gravity (9.8 m/s²)
– hf is the final height of the object
– hi is the initial height of the object
– Δt is the change in time between the initial and final positions
This equation is derived from the equations of motion, which describe the relationship between position, velocity, and acceleration in one-dimensional motion.
Applying the Equation: Assumptions and Considerations
To use the acceleration equation effectively, it’s important to consider the following assumptions and factors:
- One-Dimensional Motion: The equation assumes that the object is moving in a straight line, either upward or downward, without any lateral or horizontal motion.
- Constant Acceleration Due to Gravity: The equation assumes that the only force acting on the object is the acceleration due to gravity, which is constant at 9.8 m/s².
- Negligible Air Resistance: The equation assumes that air resistance or other external forces are negligible, and do not significantly affect the object’s motion.
- Accurate Measurements: Precise measurements of height and time are crucial for obtaining reliable results. Ensure that you use appropriate tools, such as rulers, measuring tapes, and stopwatches, and take readings carefully.
Practical Examples and Numerical Problems
Let’s explore some practical examples and numerical problems to solidify your understanding of how to find acceleration with height and time.
Example 1: Dropping an Object from a Certain Height
Suppose you drop an object from a height of 50 meters. If the object takes 2 seconds to reach the ground, calculate the acceleration of the object.
Given:
– Initial height (hi) = 50 m
– Final height (hf) = 0 m (the ground)
– Time taken (Δt) = 2 s
Substituting the values into the equation:
a = (√(2 × 9.8 × 0) - √(2 × 9.8 × 50)) / 2
a = (-√(0) - √(980)) / 2
a = (-0 - 31.32) / 2
a = -15.66 m/s²
The negative value indicates that the acceleration is directed downward, as expected for an object falling under the influence of gravity.
Example 2: Projectile Motion with Initial Velocity
Consider a scenario where an object is launched vertically upward with an initial velocity of 20 m/s. If the object reaches a maximum height of 25 meters, calculate the acceleration of the object.
Given:
– Initial velocity (vi) = 20 m/s
– Final velocity (vf) = 0 m/s (at the maximum height)
– Initial height (hi) = 0 m
– Final height (hf) = 25 m
– Time taken (Δt) = unknown
Using the equation:
a = (√(2 × 9.8 × 25) - √(2 × 9.8 × 0)) / Δt
a = (√(490) - √(0)) / Δt
a = (22.14 - 0) / Δt
a = 22.14 / Δt
To find the time taken, we can use the equation of motion:
vf = vi + at
0 = 20 - 9.8t
t = 2.04 s
Substituting the time into the acceleration equation:
a = 22.14 / 2.04
a = 10.85 m/s²
The positive value of acceleration indicates that the object is experiencing an upward acceleration, as expected for an object launched vertically upward.
Numerical Problems
- An object is dropped from a height of 80 meters. If the object takes 4 seconds to reach the ground, calculate the acceleration of the object.
- A ball is thrown vertically upward with an initial velocity of 30 m/s. If the ball reaches a maximum height of 45 meters, calculate the acceleration of the ball at the maximum height.
- A skydiver jumps from an airplane at an altitude of 3000 meters. If the skydiver reaches the ground in 60 seconds, calculate the acceleration of the skydiver during the descent.
Remember to show your work and provide the final answers with the appropriate units.
Graphical Representation and Data Analysis
To further enhance your understanding, it can be helpful to visualize the relationship between height, time, and acceleration. You can create graphs that plot the object’s position, velocity, and acceleration over time, which can provide valuable insights into the dynamics of the motion.
Additionally, collecting and analyzing data from experiments or simulations can help you validate the theoretical concepts and develop a deeper understanding of the factors that influence acceleration in vertical motion.
Limitations and Extensions
While the equation a = (√(2ghf) - √(2ghi)) / Δt is a powerful tool for calculating acceleration in one-dimensional vertical motion, it has some limitations:
- Air Resistance: The equation assumes negligible air resistance, which may not be the case for objects moving at high speeds or in dense media.
- Non-Constant Acceleration: The equation assumes a constant acceleration due to gravity, but in some cases, the acceleration may vary with height or other factors.
- Multi-Dimensional Motion: The equation is limited to one-dimensional vertical motion and cannot be directly applied to more complex, multi-dimensional scenarios.
To address these limitations, you may need to consider additional equations, such as those that account for air resistance or variable acceleration, or use more advanced techniques like numerical simulations or vector analysis.
Conclusion
Mastering the skill of finding acceleration with height and time is a crucial step in understanding one-dimensional motion in physics. By thoroughly understanding the underlying principles, equations, and practical applications, you can confidently tackle a wide range of problems and deepen your overall understanding of kinematics and dynamics.
Remember to practice regularly, experiment with different scenarios, and seek out additional resources to continuously expand your knowledge and problem-solving abilities in this important area of physics.
Reference:

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.