How to Find Acceleration with Gravity: A Comprehensive Guide

Acceleration due to gravity is a fundamental concept in physics that describes the rate of change in an object’s velocity due to the Earth’s gravitational pull. Understanding how to calculate and measure this acceleration is crucial for various applications, from analyzing the motion of falling objects to understanding the dynamics of planetary systems. In this comprehensive guide, we will delve into the factors affecting acceleration due to gravity, the equations used to calculate it, and practical methods for measuring it.

Factors Affecting Acceleration Due to Gravity

The acceleration due to gravity, denoted as “g,” is influenced by several key factors:

1. Mass of the Object (m): The mass of the object is directly proportional to the gravitational force it experiences. The heavier the object, the greater the gravitational pull it will experience.

2. Distance from the Center of Mass (r): The gravitational force is inversely proportional to the square of the distance of separation between the object and the center of mass. The larger the distance of separation, the weaker the gravitational pull.

3. Universal Gravitational Constant (G): This constant, known as the “gravitational constant,” has a value of approximately 6.673 × 10^(-11) Nm^2 kg^(-2). It represents the strength of the gravitational force between two objects.

Calculating Acceleration Due to Gravity

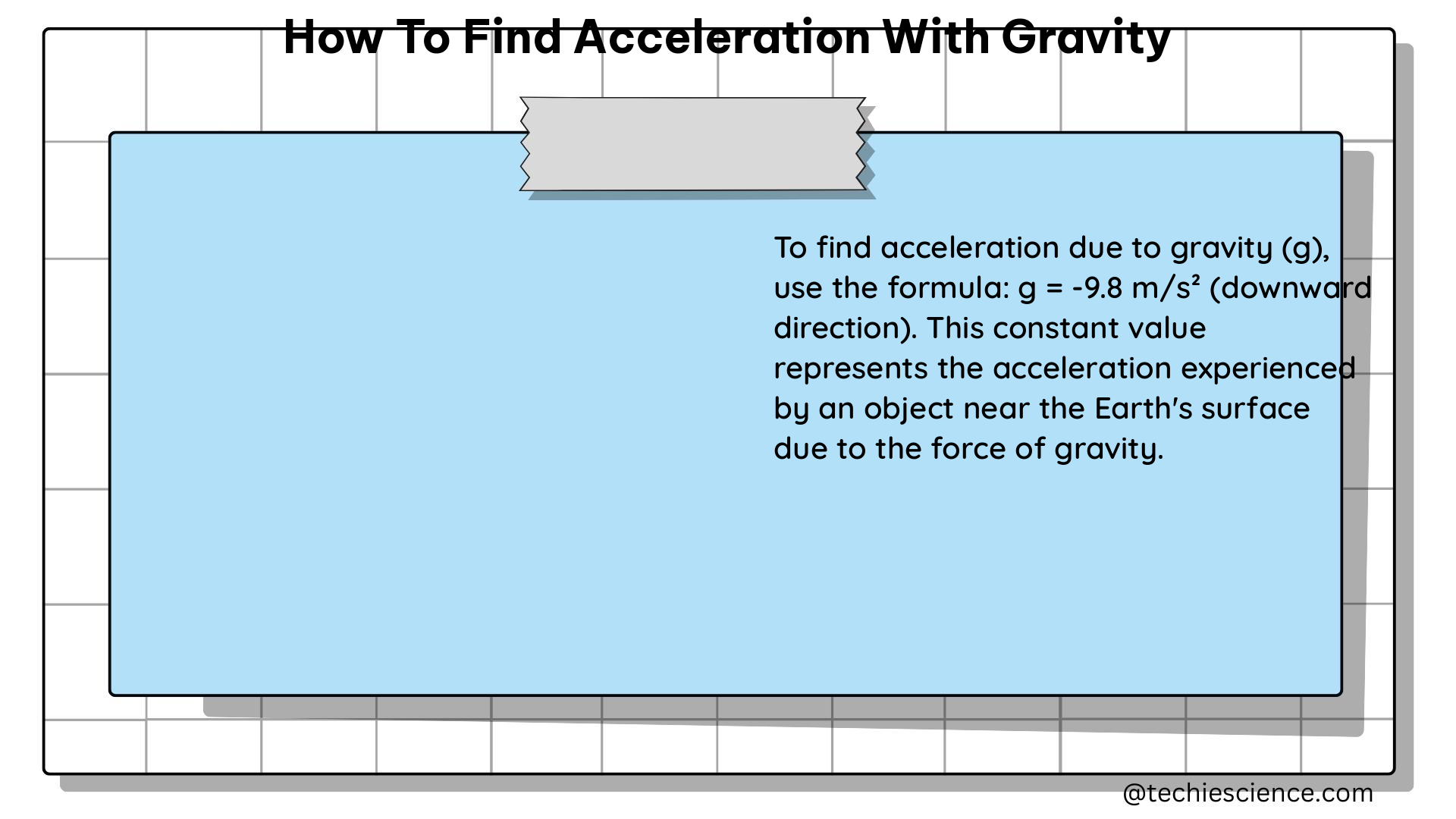
To calculate the acceleration due to gravity, we can use the following equation:

g = (G * M) / R^2

Where:
– g is the acceleration due to gravity (in m/s^2)
– G is the universal gravitational constant (6.673 × 10^(-11) Nm^2 kg^(-2))
– M is the mass of the planet or object (in kg)
– R is the radius of the planet or object (in meters)

This equation is derived from Newton’s law of universal gravitation and can be used to calculate the acceleration due to gravity on the surface of any planet or celestial body.

Example Calculation: Acceleration Due to Gravity on Earth

Given the following information:
– Mass of the Earth (M) = 5.972 × 10^24 kg
– Radius of the Earth (R) = 6,371 km = 6,371,000 m

We can calculate the acceleration due to gravity on the surface of the Earth as follows:

g = (6.673 × 10^(-11) Nm^2 kg^(-2) × 5.972 × 10^24 kg) / (6,371,000 m)^2
g ≈ 9.8 m/s^2

This result shows that the acceleration due to gravity on the surface of the Earth is approximately 9.8 m/s^2.

Measuring Acceleration Due to Gravity

There are several methods for measuring the acceleration due to gravity, each with its own advantages and limitations. Two common methods are the free fall method and the use of kinematic equations.

Free Fall Method

The free fall method involves measuring the height of an object’s fall (h) and the time it takes to fall (t). Using these measurements, the acceleration due to gravity can be calculated using the following equation:

g = 2h / t^2

This method assumes that the object is in free fall, meaning it is only subject to the Earth’s gravitational force and is not affected by air resistance or other external forces.

Kinematic Equations

Kinematic equations can also be used to determine the acceleration due to gravity. These equations describe the motion of an object under the influence of gravity, and they can be used to solve for the acceleration due to gravity (g) if other variables are known.

The relevant kinematic equations for free fall are:

v = u + gt
s = ut + (1/2)gt^2
v^2 = u^2 + 2gs

Where:
– v is the final velocity (m/s)
– u is the initial velocity (m/s)
– g is the acceleration due to gravity (m/s^2)
– t is the time (s)
– s is the displacement (m)

By rearranging these equations and solving for g, you can determine the acceleration due to gravity.

Advanced Considerations

Variations in Acceleration Due to Gravity

The acceleration due to gravity can vary slightly depending on the location on Earth. This is due to factors such as latitude, altitude, and the Earth’s rotation. For example, the acceleration due to gravity is slightly higher at the poles than at the equator due to the Earth’s oblate spheroid shape.

Acceleration Due to Gravity on Other Planets

The acceleration due to gravity on other planets can be calculated using the same equation as for Earth, but with the appropriate values for the planet’s mass and radius. This allows for the determination of the acceleration due to gravity on different celestial bodies, which is crucial for understanding the dynamics of planetary systems and the motion of objects within them.

Experimental Techniques for Measuring Acceleration Due to Gravity

In addition to the free fall method and kinematic equations, there are more advanced experimental techniques for measuring the acceleration due to gravity, such as the use of pendulums, torsion balances, and gravimeters. These methods can provide more precise measurements and are often used in scientific research and geophysical surveys.

Conclusion

Understanding the factors that affect acceleration due to gravity and the methods for calculating and measuring it is essential for a wide range of applications in physics, engineering, and astronomy. By mastering these concepts, you can gain a deeper understanding of the fundamental principles governing the motion of objects under the influence of gravity, and apply this knowledge to solve complex problems and advance scientific understanding.

References

1. Intmath. (n.d.). Calculating Acceleration Due to Gravity on a Plane. Retrieved from https://www.intmath.com/blog/mathematics/calculating-acceleration-due-to-gravity-on-a-plane-12517
2. Weber State University. (n.d.). Gravity Lab. Retrieved from https://physics.weber.edu/palen/clearinghouse/homeworks/Gravity_Lab.html
3. Southern Methodist University. (n.d.). Acceleration Due to Gravity. Retrieved from https://www.physics.smu.edu/~ryszard/1313fa97/1313-Acceler_.PDF
4. Socratic. (n.d.). How is Acceleration Due to Gravity Calculated? Retrieved from https://socratic.org/questions/how-is-acceleration-due-to-gravity-calculated
5. Study.com. (n.d.). How to Calculate the Acceleration Due to Gravity on a Different Planet. Retrieved from https://study.com/skill/learn/how-to-calculate-the-acceleration-due-to-gravity-on-a-different-planet-explanation.html