Summary
Determining acceleration from final velocity and distance is a fundamental concept in physics. This comprehensive guide will walk you through the step-by-step process, providing detailed explanations, formulas, examples, and numerical problems to help you master this essential skill.
Understanding the Kinematic Equation
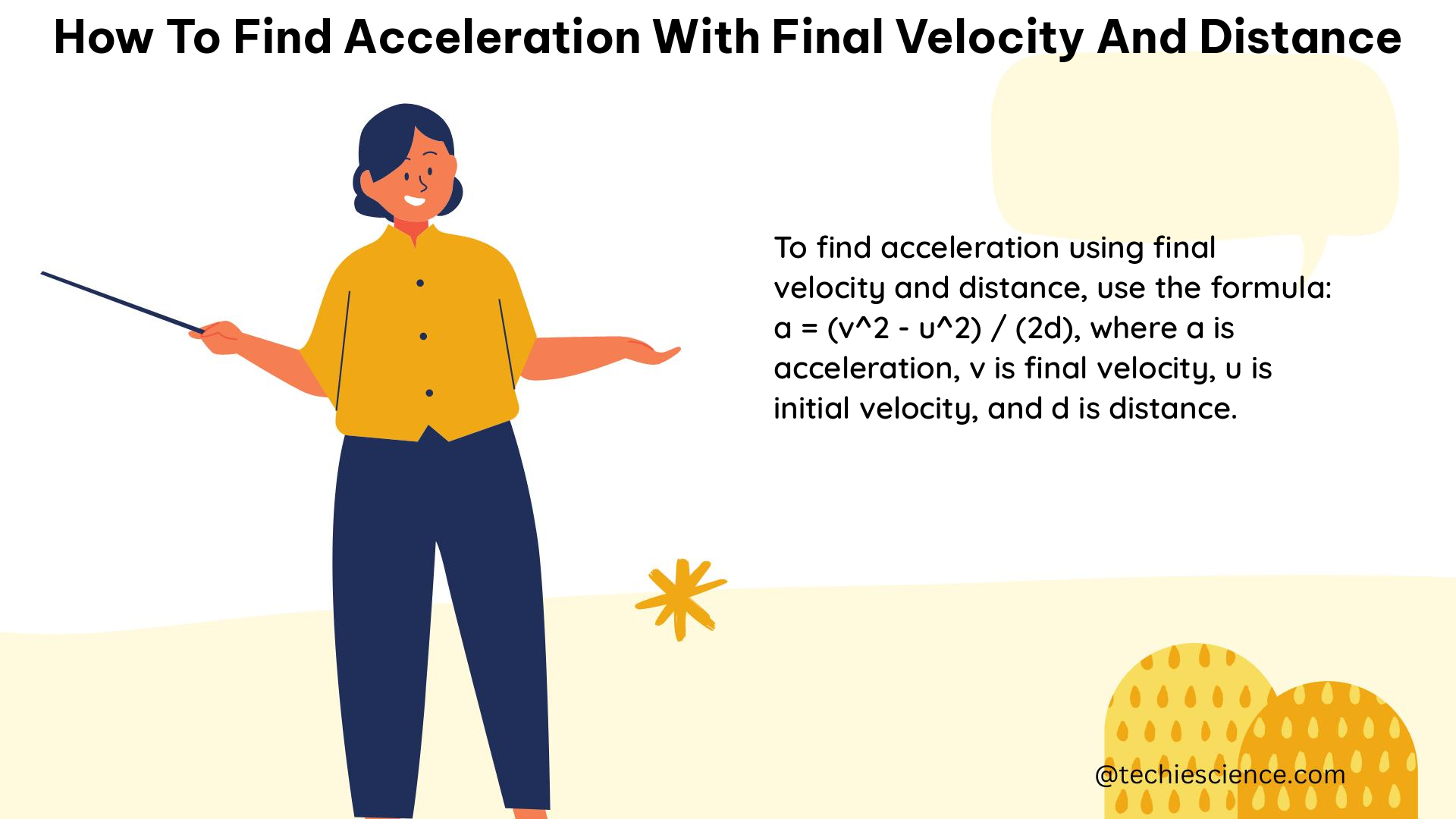
The formula used to find acceleration with final velocity and distance is:
a = (v^2 - u^2) / (2d)
Where:
– a is the acceleration (in m/s^2)
– v is the final velocity (in m/s)
– u is the initial velocity (in m/s)
– d is the distance traveled (in m)
This equation is derived from the kinematic equations of motion, which describe the relationship between an object’s position, velocity, and acceleration.
Step-by-Step Approach
To find the acceleration using the final velocity and distance, follow these steps:
-
Identify the Initial and Final Velocities: Determine the object’s initial velocity (
u) and final velocity (v). These values should be given or can be calculated from the provided information. -
Identify the Distance Traveled: Determine the distance (
d) the object has traveled between the initial and final velocities. -
Plug the Values into the Formula: Substitute the values of
v,u, anddinto the formulaa = (v^2 - u^2) / (2d)and solve for the accelerationa. -
Interpret the Result: Analyze the sign of the calculated acceleration. A positive value indicates acceleration, while a negative value indicates deceleration (or negative acceleration).
Examples and Numerical Problems
Example 1: Constant Acceleration in a Straight Line
A car starts from rest (u = 0 m/s) and travels a distance of 50 meters. If the car’s final velocity is 20 m/s, calculate the acceleration.
Given:
– Initial velocity, u = 0 m/s
– Final velocity, v = 20 m/s
– Distance, d = 50 m
Substituting the values into the formula:
a = (v^2 - u^2) / (2d)
a = (20^2 - 0^2) / (2 × 50)
a = 400 / 100
a = 4 m/s^2
The acceleration of the car is 4 m/s^2.
Example 2: Deceleration with Known Final Velocity and Distance
A runner starts at an initial velocity of 10 m/s and covers a distance of 100 meters. If the runner’s final velocity is 8.5 m/s, calculate the acceleration.
Given:
– Initial velocity, u = 10 m/s
– Final velocity, v = 8.5 m/s
– Distance, d = 100 m
Substituting the values into the formula:
a = (v^2 - u^2) / (2d)
a = (8.5^2 - 10^2) / (2 × 100)
a = (72.25 - 100) / 200
a = -27.75 / 200
a = -0.13875 m/s^2
The negative sign indicates that the runner is decelerating at a rate of 0.13875 m/s^2.
Numerical Problem 1
A ball is thrown upward with an initial velocity of 20 m/s. If the ball reaches a maximum height of 25 meters, calculate the acceleration of the ball.
Given:
– Initial velocity, u = 20 m/s
– Final velocity, v = 0 m/s (at the maximum height)
– Distance, d = 25 m
Substituting the values into the formula:
a = (v^2 - u^2) / (2d)
a = (0^2 - 20^2) / (2 × 25)
a = (-400) / 50
a = -8 m/s^2
The negative sign indicates that the ball is decelerating due to the force of gravity.
Numerical Problem 2
A car accelerates from 0 m/s to 30 m/s over a distance of 50 meters. Calculate the acceleration of the car.
Given:
– Initial velocity, u = 0 m/s
– Final velocity, v = 30 m/s
– Distance, d = 50 m
Substituting the values into the formula:
a = (v^2 - u^2) / (2d)
a = (30^2 - 0^2) / (2 × 50)
a = 900 / 100
a = 9 m/s^2
The acceleration of the car is 9 m/s^2.
Important Considerations
-
Constant Acceleration Assumption: The formula
a = (v^2 - u^2) / (2d)assumes that the acceleration is constant throughout the motion. If the acceleration is not constant, more complex equations of motion may be required. -
Straight-Line Motion: The formula assumes that the motion is in a straight line. If the motion involves curved paths or changes in direction, additional considerations may be necessary.
-
Unit Conversions: Ensure that the units of velocity (m/s) and distance (m) are consistent when using the formula. If the units are different, appropriate conversions should be performed before applying the formula.
-
Positive and Negative Acceleration: The sign of the calculated acceleration indicates the direction of the motion. A positive value represents acceleration, while a negative value represents deceleration or negative acceleration.
-
Limitations and Assumptions: The formula and examples provided assume ideal conditions and simplifications. In real-world scenarios, additional factors such as air resistance, friction, or other external forces may need to be considered for a more accurate analysis.
Reference
- Using Kinematic Equations to Solve for an Unknown Acceleration
- How would I find acceleration from distance and velocity
- Acceleration (a) is the change in velocity (Δv) over the change in time (Δt)
- How to Calculate Acceleration – 3 Formulas You Must Know
- Lesson Explainer: Acceleration over a Distance Physics – Nagwa

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.