How to Find Acceleration with Angle and Coefficient of Kinetic Friction 2

Summary

Determining the acceleration of an object moving on a surface with a known angle and coefficient of kinetic friction is a fundamental concept in classical mechanics. This comprehensive guide will walk you through the step-by-step process of calculating the acceleration, including deriving the necessary equations, applying them to specific examples, and providing detailed explanations to help you master this important skill.

Understanding the Fundamentals

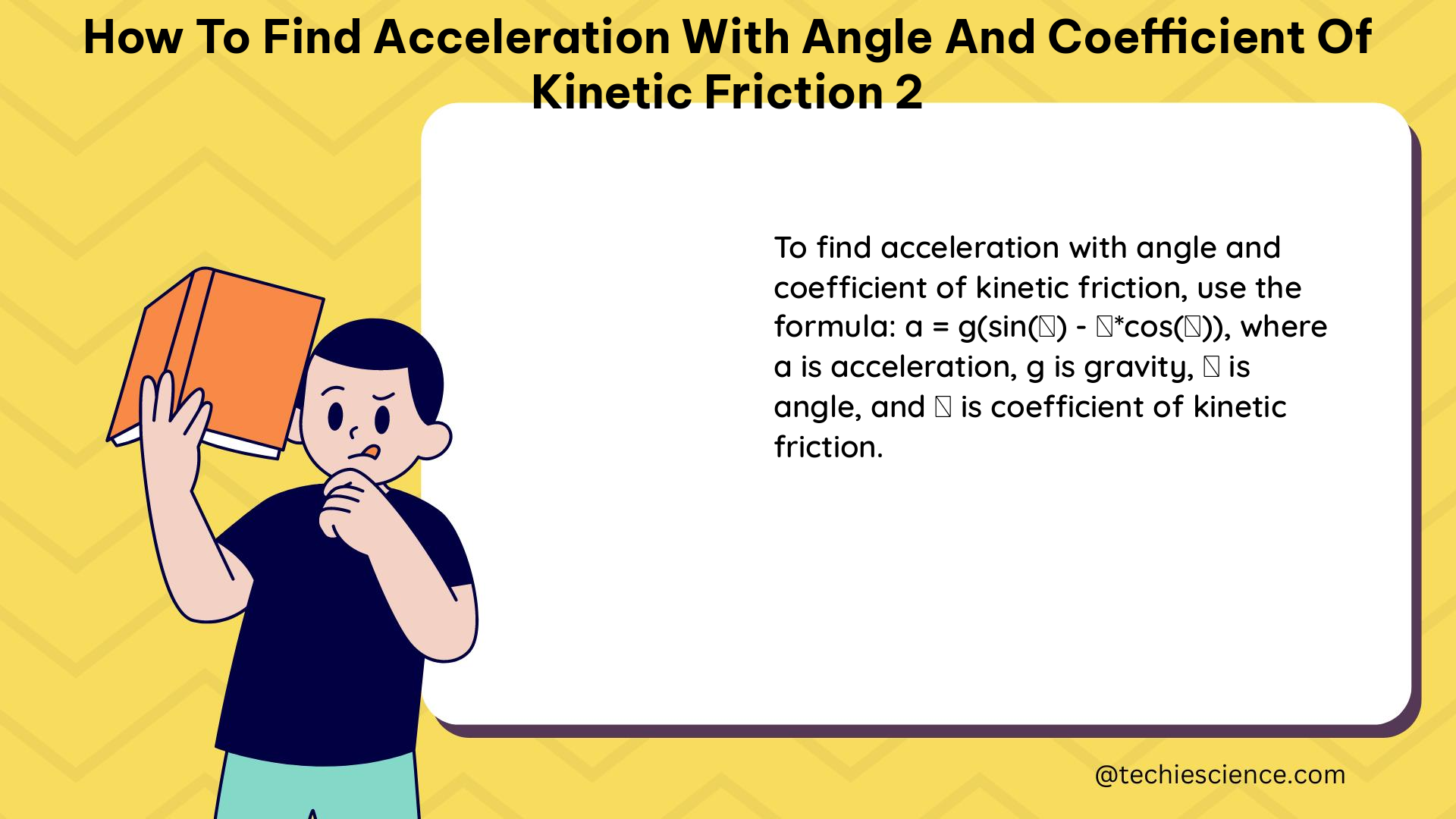
To find the acceleration of an object moving on a surface with a known angle and coefficient of kinetic friction, we need to consider the forces acting on the object and apply Newton’s laws of motion.

The key forces involved in this scenario are:

1. Applied Force (F): The force applied to the object, which is responsible for its motion.
2. Kinetic Friction Force (F_k): The force that opposes the motion of the object due to the roughness of the surface.
3. Normal Force (N): The force exerted by the surface on the object, perpendicular to the surface.
4. Gravitational Force (mg): The force acting on the object due to gravity.

The relationship between these forces and the object’s acceleration can be expressed using the following equation:

F - F_k = m * a

where:
– F is the applied force
– F_k is the kinetic friction force
– m is the mass of the object
– a is the acceleration of the object

Calculating the Kinetic Friction Force

The kinetic friction force, F_k, can be calculated using the following equation:

F_k = μ_k * N

where:
– μ_k is the coefficient of kinetic friction
– N is the normal force acting on the object

The normal force, N, can be calculated using the following equation:

N = m * g * cos(θ)

where:
– m is the mass of the object
– g is the acceleration due to gravity (9.81 m/s²)
– θ is the angle of the surface relative to the horizontal

Substituting the expression for the normal force, we get:

F_k = μ_k * m * g * cos(θ)

Calculating the Acceleration

Now, we can substitute the expressions for the kinetic friction force and the normal force into the original equation:

F - μ_k * m * g * cos(θ) = m * a

Rearranging the equation, we get the final expression for the acceleration:

a = (F - μ_k * m * g * cos(θ)) / m

This equation allows us to calculate the acceleration of an object moving on a surface with a known angle and coefficient of kinetic friction.

Examples and Applications

Let’s consider a few examples to illustrate the application of this equation.

Example 1: Pushing a Box on a Horizontal Surface

Suppose a student pushes a box with a force of 15 N on a horizontal surface. The box has a mass of 6 kg, and the coefficient of kinetic friction between the box and the surface is 0.25.

To find the acceleration of the box, we can use the following steps:

1. Identify the given values:
2. Applied force, F = 15 N
3. Mass of the box, m = 6 kg
4. Coefficient of kinetic friction, μ_k = 0.25

5. Angle of the surface, θ = 0° (horizontal)

6. Calculate the kinetic friction force:
   F_k = μ_k * m * g * cos(θ)
F_k = 0.25 * 6 kg * 9.81 m/s² * cos(0°)
F_k = 14.72 N

7. Calculate the acceleration:
   a = (F - F_k) / m
a = (15 N - 14.72 N) / 6 kg
a = 0.28 m/s²

Therefore, the acceleration of the box is 0.28 m/s².

Example 2: Pushing a Puck on Ice

A hockey player pushes a puck with a force of 30 N on an ice surface. The puck has a mass of 2 kg, and the coefficient of kinetic friction between the puck and the ice is 0.1.

To find the acceleration of the puck, we can use the following steps:

1. Identify the given values:
2. Applied force, F = 30 N
3. Mass of the puck, m = 2 kg
4. Coefficient of kinetic friction, μ_k = 0.1

5. Angle of the surface, θ = 0° (horizontal)

6. Calculate the kinetic friction force:
   F_k = μ_k * m * g * cos(θ)
F_k = 0.1 * 2 kg * 9.81 m/s² * cos(0°)
F_k = 1.962 N

7. Calculate the acceleration:
   a = (F - F_k) / m
a = (30 N - 1.962 N) / 2 kg
a = 14.019 m/s²

Therefore, the acceleration of the puck is 14.019 m/s².

Additional Considerations

1. Inclined Surfaces: If the surface is inclined at an angle θ relative to the horizontal, the normal force and the kinetic friction force will be affected by the angle. In this case, the equation for the acceleration becomes:

a = (F - μ_k * m * g * cos(θ)) / m

1. Static Friction: In some cases, the object may start from rest, and you need to consider the static friction force instead of the kinetic friction force. The static friction force is generally higher than the kinetic friction force, and the equation for the acceleration would need to be modified accordingly.

2. Numerical Examples: To further solidify your understanding, it’s recommended to practice solving numerical problems involving the calculation of acceleration with angle and coefficient of kinetic friction. This will help you develop a better intuition for the relationships between the various parameters and their impact on the final result.

3. Experimental Verification: If possible, you can conduct simple experiments to measure the acceleration of an object moving on a surface with a known angle and coefficient of kinetic friction. This hands-on experience can help you validate the theoretical concepts and gain a deeper understanding of the underlying physics.

Conclusion

Determining the acceleration of an object moving on a surface with a known angle and coefficient of kinetic friction is a fundamental skill in classical mechanics. By understanding the relationships between the forces involved and applying the appropriate equations, you can accurately calculate the acceleration of the object. This knowledge is essential for solving a wide range of physics problems, from everyday situations to more complex engineering applications.

References

1. Calculating Horizontal Acceleration in Systems with Friction
2. Friction and Newton’s Laws of Motion
3. Friction Example Problems
4. Inclined Plane with Friction
5. Calculating Acceleration on an Inclined Plane