How to Find Acceleration of Gravity: A Comprehensive Guide

by

Summary

Determining the acceleration of gravity, commonly denoted as “g,” is a fundamental task in physics. This comprehensive guide explores four distinct methods to measure and calculate the acceleration of gravity, providing detailed technical specifications, formulas, and examples to help physics students and enthusiasts understand this crucial concept thoroughly.

Method 1: Measuring ‘g’ Using a Golf Ball and Stopwatch

how to find acceleration of gravity

Materials

  • Golf ball
  • Stopwatch with 1/100 of a second precision
  • String and rulers to measure height

Procedure

  1. Choose a suitable location for dropping the golf ball, ensuring a height that minimizes air resistance.
  2. Measure the distance the ball will fall (in meters).
  3. Time the ball’s fall at least 20 times, recording the time it takes for the ball to reach the ground.
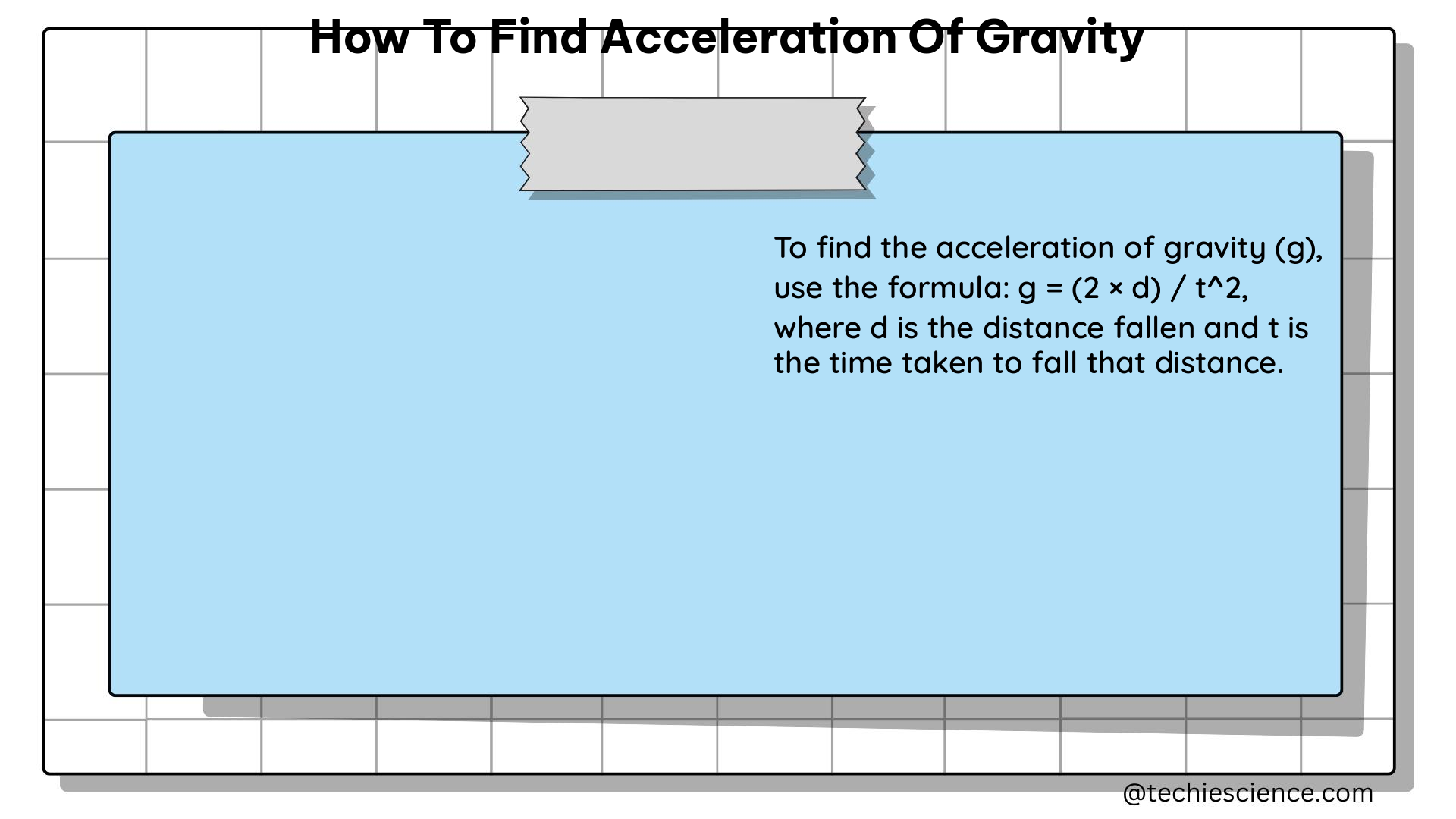
  4. Calculate the earth’s acceleration due to gravity using the relation:
    g = (2 * h) / t^2
    where h is the height of the fall and t is the average time of fall.

Uncertainty Estimation

  1. Calculate the random uncertainty:
    Δt = (longest time - shortest time) / 2
  2. Use this uncertainty to estimate the range of possible values for g:
    g_low = (2 * h) / (t + Δt)^2
    g_high = (2 * h) / (t - Δt)^2

Method 2: Calculating Acceleration Due to Gravity Using Gravitational Constant

Formula

The acceleration due to gravity can be calculated using the formula:

g = (G * M) / R^2

where G is the gravitational constant (6.67 × 10^(-11) N m^2 kg^2), M is the mass of the Earth (5.972 × 10^24 kg), and R is the radius of the Earth (6,371 km).

Calculation

Substituting the values:

g = (6.67 × 10^(-11) × 5.972 × 10^24) / (6,371,000)^2 ≈ 9.8 m/s^2

Method 3: Calculating Acceleration Due to Gravity on a Plane

Formula

The acceleration due to gravity on a plane can be calculated using the formula:

g = (G * M) / R^2

where G is the gravitational constant, M is the mass of the plane, and R is the radius of the plane.

Example

For the moon, with a radius of 1.64 × 10^6 m and a mass of 7.24 × 10^22 kg:

g = (6.673 × 10^(-11) × 7.24 × 10^22) / (1.64 × 10^6)^2 ≈ 1.796 m/s^2

Method 4: Measuring Acceleration Due to Gravity Using One-Dimensional Motion

Formula

The acceleration due to gravity can be calculated using the equation for one-dimensional motion:

x(t) = (1/2) * g * t^2

where x(t) is the position as a function of time, g is the acceleration due to gravity, and t is time.

Procedure

  1. Measure the distance the object falls and the time it takes to fall.
  2. Use the equation to solve for g:
    g = (2 * x) / t^2

Additional Considerations

  • The methods presented provide a range of techniques to measure and calculate the acceleration of gravity, each with its own advantages and limitations.
  • Factors such as air resistance, measurement precision, and environmental conditions can impact the accuracy of the results.
  • It is recommended to perform multiple trials and take the average to improve the reliability of the measurements.
  • Comparing the results obtained from different methods can help validate the accuracy of the calculations.

References

  1. Gravity Lab – Weber State University. (n.d.). Retrieved from https://physics.weber.edu/palen/clearinghouse/homeworks/Gravity_Lab.html
  2. How is acceleration due to gravity calculated? – Socratic. (2018, May 2). Retrieved from https://socratic.org/questions/how-is-acceleration-due-to-gravity-calculated
  3. Calculating Acceleration Due to Gravity on a Plane – IntMath. (2020, October 8). Retrieved from https://www.intmath.com/blog/mathematics/calculating-acceleration-due-to-gravity-on-a-plane-12517