Calculating the acceleration of an object given the coefficient of kinetic friction is a fundamental concept in classical mechanics. This comprehensive guide will provide you with the necessary tools and techniques to master this topic, including detailed explanations, formulas, examples, and numerical problems.
Understanding the Relationship Between Acceleration, Friction, and Gravity
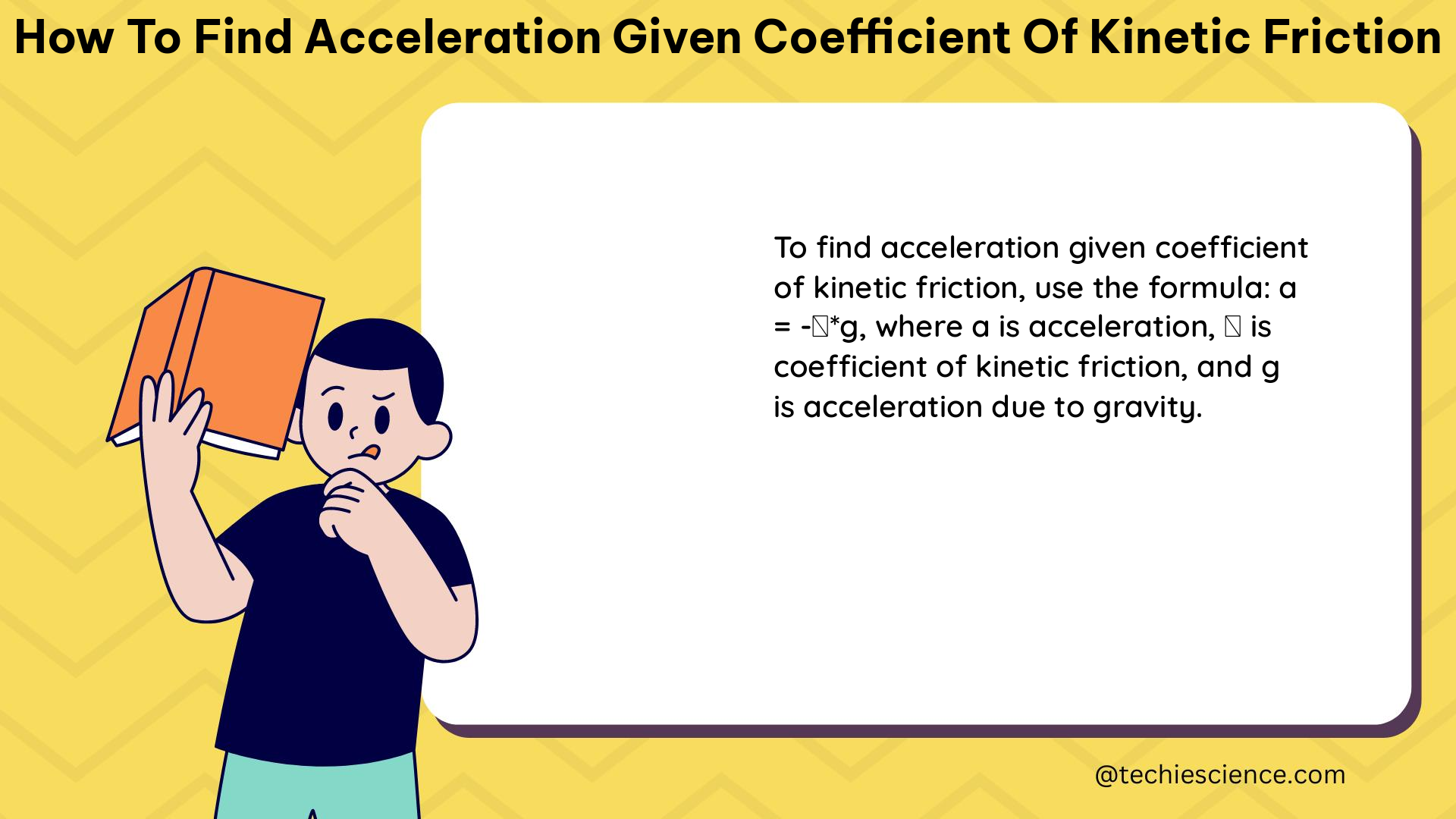
The formula to find the acceleration of an object given the coefficient of kinetic friction is:
a = μk * g
Where:
– a is the acceleration of the object
– μk is the coefficient of kinetic friction
– g is the acceleration due to gravity (approximately 9.8 m/s²)
This formula is derived from the fact that the net force acting on the object is the difference between the force of gravity and the force of kinetic friction. The acceleration of the object is then determined by the net force and the mass of the object, as per Newton’s second law of motion.
It’s important to note that this formula assumes that the only forces acting on the object are gravity, friction, and the normal force from the surface of the incline. If there are other forces acting on the object, such as a applied force or air resistance, the formula would need to be modified accordingly.
Coefficient of Kinetic Friction
The coefficient of kinetic friction, denoted as μk, is a dimensionless quantity that represents the ratio of the force of kinetic friction to the normal force between two surfaces in relative motion. The value of the coefficient of kinetic friction depends on the materials of the two surfaces in contact and can range from 0 to 1.
Some common values of the coefficient of kinetic friction are:
| Material Combination | Coefficient of Kinetic Friction (μk) |
|---|---|
| Steel on steel | 0.10 – 0.15 |
| Aluminum on steel | 0.45 |
| Rubber on concrete | 0.50 – 0.80 |
| Ice on ice | 0.03 |
It’s important to note that the coefficient of kinetic friction can vary depending on the specific conditions, such as surface roughness, temperature, and the presence of lubricants or contaminants.
Calculating Acceleration Using the Formula
To use the formula a = μk * g to find the acceleration of an object, you need to know the value of the coefficient of kinetic friction and the acceleration due to gravity.
For example, let’s say you have a box sliding down a ramp with a coefficient of kinetic friction of 0.3. You can calculate the acceleration of the box using the formula:
a = 0.3 * 9.8 m/s²
a = 2.94 m/s²
So, the acceleration of the box is 2.94 m/s².
Numerical Problems
- A 5 kg block is sliding down a ramp with a coefficient of kinetic friction of 0.2. Calculate the acceleration of the block.
Given:
– Mass of the block, m = 5 kg
– Coefficient of kinetic friction, μk = 0.2
– Acceleration due to gravity, g = 9.8 m/s²
Using the formula a = μk * g:
a = 0.2 * 9.8 m/s²
a = 1.96 m/s²
Therefore, the acceleration of the block is 1.96 m/s².
- A 10 kg object is sliding on a horizontal surface with a coefficient of kinetic friction of 0.4. Calculate the acceleration of the object.
Given:
– Mass of the object, m = 10 kg
– Coefficient of kinetic friction, μk = 0.4
– Acceleration due to gravity, g = 9.8 m/s²
Using the formula a = μk * g:
a = 0.4 * 9.8 m/s²
a = 3.92 m/s²
Therefore, the acceleration of the object is 3.92 m/s².
Applying Newton’s Second Law
In addition to the formula a = μk * g, you can also use Newton’s second law of motion to find the acceleration of an object given the net force and the mass of the object.
The formula for Newton’s second law is:
Fnet = m * a
Where:
– Fnet is the net force acting on the object
– m is the mass of the object
– a is the acceleration of the object
Rearranging the formula to solve for acceleration, we get:
a = Fnet / m
To find the net force acting on the object, you need to consider all the forces acting on the object and add up the forces in the direction of motion. For example, if an object is being pushed to the right with a force of 10 N and experiencing a frictional force to the left of 5 N, the net force acting on the object is 5 N to the right.
Using this formula, you can find the acceleration of an object given the net force and the mass of the object. However, if you are given the coefficient of kinetic friction, it is often easier to use the formula a = μk * g to find the acceleration.
Conclusion
In this comprehensive guide, we have explored the fundamental concepts and techniques for finding the acceleration of an object given the coefficient of kinetic friction. By understanding the relationship between acceleration, friction, and gravity, as well as the role of the coefficient of kinetic friction, you can now confidently solve a wide range of problems in classical mechanics.
Remember, the key to mastering this topic is to practice applying the formulas and solving numerical problems. Engage in hands-on experiments, analyze real-world scenarios, and continuously challenge yourself to deepen your understanding of this important concept.
Reference:

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.