How to Find Acceleration from Distance: A Comprehensive Guide

Acceleration is a fundamental concept in physics that describes the rate of change in an object’s velocity over time. Determining acceleration from distance is a crucial skill for students and professionals in various fields, including physics, engineering, and transportation. In this comprehensive guide, we will delve into the step-by-step process, formulas, and theoretical explanations to help you master the art of finding acceleration from distance.

The Acceleration Formula

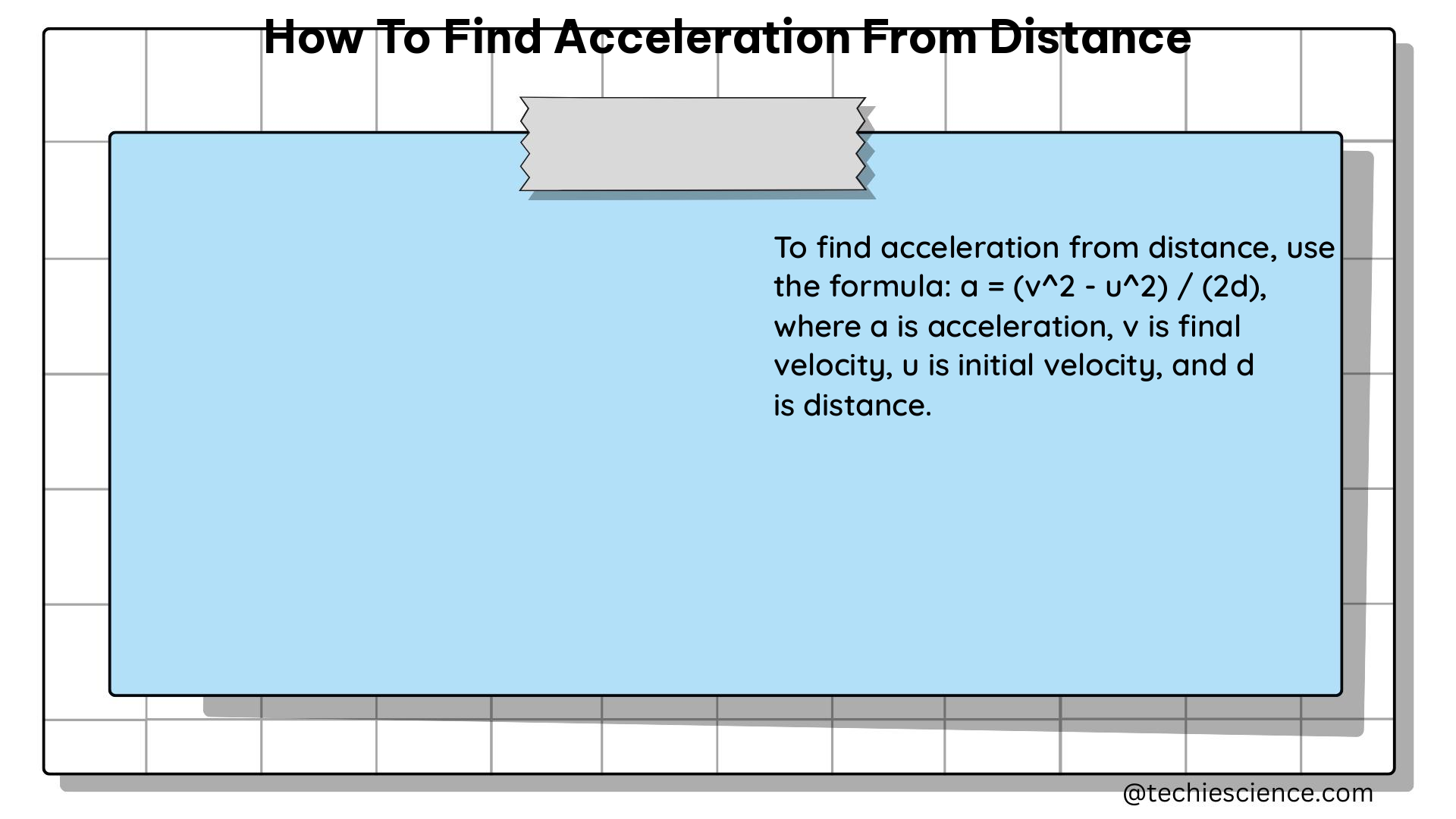
The formula to find acceleration from distance is:

[a = \frac{2 \Delta d}{\Delta t^2}]

Where:
– a is the acceleration of the object (in m/s²)
– Δd is the change in distance or displacement (in meters)
– Δt is the change in time (in seconds)

This formula is derived from the kinematic equations of motion, which describe the relationship between position, velocity, and acceleration.

Step-by-Step Guide to Finding Acceleration from Distance

1. Identify the Initial and Final Velocities: Determine the initial velocity (v_i) and final velocity (v_f) of the object. This information is crucial for calculating the change in velocity, which is a key component in the acceleration formula.

2. Calculate the Change in Velocity: Calculate the change in velocity (Δv) by subtracting the initial velocity from the final velocity:

[\Delta v = v_f – v_i]

1. Measure the Time: Measure the time (Δt) over which the acceleration occurs. This time interval should be the same as the one used to calculate the change in distance or displacement.

2. Calculate Acceleration: Use the formula to calculate the acceleration (a):

[a = \frac{\Delta v}{\Delta t}]

Alternatively, you can use the formula:

[a = \frac{2 \Delta d}{\Delta t^2}]

This formula is derived from the kinematic equations and directly relates the acceleration to the change in distance and time.

Example: Calculating Acceleration in a Drag Race

Suppose you are a drag racer and you want to find your acceleration down the dragway. You know the distance you traveled (Δd = 402 meters) and the time it took (Δt = 5.5 seconds). You can use the formula to find your acceleration:

[a = \frac{2 \Delta d}{\Delta t^2} = \frac{2 \times 402}{5.5^2} \approx 27 \text{ meters per second squared}]

In this example, the acceleration of the drag racer is approximately 27 meters per second squared (m/s²).

Theoretical Explanation: Taylor Series Expansion

Acceleration can be understood through the concept of Taylor series expansions, which relate position, velocity, and acceleration. The acceleration formula can be derived from the Taylor series expansion of position with respect to time:

[x(t) = x_0 + v_0 t + \frac{1}{2} a_0 t^2 + \dots]

Where:
– x(t) is the position of the object at time t
– x_0 is the initial position of the object
– v_0 is the initial velocity of the object
– a_0 is the initial acceleration of the object

By differentiating this equation twice with respect to time, we can derive the acceleration formula:

[a = \frac{d^2 x}{dt^2}]

This theoretical explanation helps us understand the underlying principles behind the acceleration formula and its relationship to position and velocity.

Units of Acceleration

Acceleration is typically measured in units of meters per second squared (m/s²), but it can also be expressed in other units such as:

• Miles per hour per second (mph/s)
• Kilometers per hour squared (km/h²)
• Feet per second squared (ft/s²)

The choice of units depends on the context and the preferences of the field or application.

Practical Applications and Considerations

Determining acceleration from distance is essential in various fields, including:

1. Transportation: Calculating the acceleration of vehicles, such as cars, trains, and airplanes, is crucial for understanding their performance, safety, and energy efficiency.

2. Sports and Athletics: Analyzing the acceleration of athletes, such as sprinters, jumpers, and cyclists, can provide valuable insights into their technique and training.

3. Engineering: Acceleration data is crucial for the design and analysis of mechanical systems, structures, and vehicles.

4. Physics and Astronomy: Acceleration is a fundamental concept in the study of motion, dynamics, and the behavior of celestial bodies.

When applying the acceleration formula, it’s important to consider the following:

• Accuracy of measurements: Ensure that the measurements of distance and time are as precise as possible to minimize errors in the calculated acceleration.
• Assumptions and limitations: The formula assumes constant acceleration, which may not always be the case in real-world scenarios.
• Contextual factors: Consider the specific conditions and factors that may influence the acceleration, such as friction, air resistance, or external forces.

Conclusion

Finding acceleration from distance is a crucial skill in physics and various related fields. By understanding the formula, the step-by-step process, and the theoretical underpinnings, you can confidently tackle problems involving the determination of acceleration from distance measurements. This comprehensive guide has provided you with the necessary tools and knowledge to become an expert in this area. Remember to practice regularly, apply the concepts to real-world examples, and continuously expand your understanding of this fundamental topic in physics.

References

1. Dummies – How to Calculate Acceleration: This article provides a detailed explanation of how to calculate acceleration, including the formula and examples.

2. Physics Stack Exchange – Can you completely explain acceleration to me?: This discussion provides a detailed explanation of acceleration, including its relationship to velocity and time, and how it can be understood through Taylor series expansions.

3. Khan Academy – Acceleration (video): This video explains acceleration as the change in velocity over time and provides examples of how to calculate it.

4. MIT OpenCourseWare – Kinematics and Dynamics: This lecture note from MIT provides a comprehensive overview of kinematics, including the concepts of position, velocity, and acceleration.

5. University of Colorado Boulder – Kinematic Equations and Problem-Solving: This interactive simulation from the University of Colorado Boulder allows you to explore the relationships between position, velocity, and acceleration.