How to Find Acceleration and Force: A Comprehensive Guide

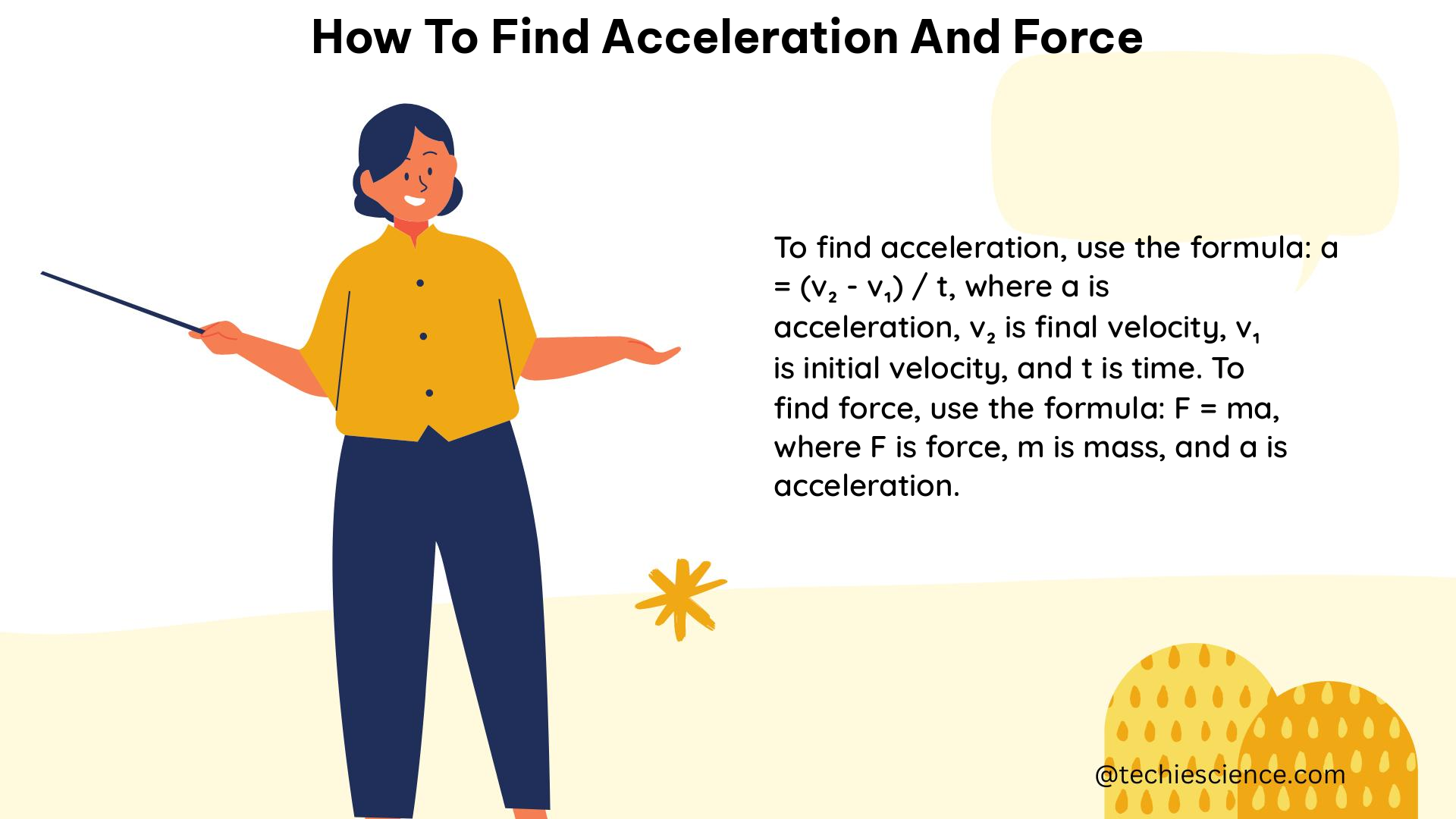
In the realm of classical mechanics, understanding the concepts of acceleration and force is crucial for analyzing the motion of objects and predicting their behavior. This comprehensive guide will delve into the step-by-step process of calculating acceleration and force, providing you with a thorough understanding of the underlying principles and practical applications.

Identifying the Given Quantities

The first step in finding acceleration and force is to identify the relevant quantities provided in the problem statement. These typically include:

1. Mass (m): The mass of the object in kilograms (kg).
2. Force (F): The applied force acting on the object, measured in newtons (N).
3. Coefficient of Friction (μ): The dimensionless coefficient that represents the frictional force between the object and the surface.
4. Acceleration due to Gravity (g): The acceleration experienced by an object due to the Earth’s gravitational pull, which is approximately 9.81 m/s².

Accurately identifying these quantities is crucial for the subsequent calculations.

Calculating the Force of Friction

If there is friction acting on the object, it is necessary to determine the force of friction (F_k) using the following formula:

F_k = μ × m × g

Where:
– F_k is the force of friction (in newtons, N)
– μ is the coefficient of friction (dimensionless)
– m is the mass of the object (in kilograms, kg)
– g is the acceleration due to gravity (in meters per second squared, m/s²)

This step is important because the force of friction must be subtracted from the applied force to find the net force acting on the object.

Calculating the Net Force

The net force (F_net) acting on the object is the difference between the applied force (F_app) and the force of friction (F_k). The formula for calculating the net force is:

F_net = F_app – F_k

Where:
– F_net is the net force (in newtons, N)
– F_app is the applied force (in newtons, N)
– F_k is the force of friction (in newtons, N)

Determining the net force is crucial for the final step of calculating the acceleration.

Calculating the Acceleration

Once the net force (F_net) is known, the acceleration (a) of the object can be calculated using Newton’s second law of motion, which states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. The formula for calculating acceleration is:

a = F_net / m

Where:
– a is the acceleration (in meters per second squared, m/s²)
– F_net is the net force (in newtons, N)
– m is the mass of the object (in kilograms, kg)

This formula allows you to determine the acceleration of the object based on the net force and its mass.

Examples and Numerical Problems

Let’s apply the concepts we’ve learned to solve some examples and numerical problems.

Example 1: A student pushes a chair on the floor of a classroom with a force of 15 N. The chair has a mass of 6 kg and a coefficient of kinetic friction with the floor of 0.25. What is the acceleration of the chair?

Solution:
1. Identify the given quantities:
– Mass (m) = 6 kg
– Applied force (F_app) = 15 N
– Coefficient of kinetic friction (μ_k) = 0.25
2. Calculate the force of friction:
– F_k = μ_k × m × g = 0.25 × 6 kg × 9.81 m/s² = 14.72 N
3. Calculate the net force:
– F_net = F_app – F_k = 15 N – 14.72 N = 0.28 N
4. Calculate the acceleration:
– a = F_net / m = 0.28 N / 6 kg = 0.0467 m/s²

Example 2: A box of mass 20 kg is placed on a horizontal surface with a coefficient of static friction of 0.3. A force of 50 N is applied to the box. What is the acceleration of the box?

Solution:
1. Identify the given quantities:
– Mass (m) = 20 kg
– Applied force (F_app) = 50 N
– Coefficient of static friction (μ_s) = 0.3
2. Calculate the force of static friction:
– F_s = μ_s × m × g = 0.3 × 20 kg × 9.81 m/s² = 58.86 N
3. Calculate the net force:
– Since the applied force (50 N) is less than the force of static friction (58.86 N), the box will not move, and the acceleration is zero.

These examples demonstrate the step-by-step process of calculating acceleration and force using the formulas and principles discussed earlier.

Additional Considerations

1. Inclined Planes: When dealing with objects on inclined planes, the force of friction and the net force must be calculated considering the angle of the incline.
2. Circular Motion: For objects undergoing circular motion, the centripetal force and the resulting acceleration must be taken into account.
3. Newton’s Laws of Motion: Understanding the three laws of motion (inertia, acceleration, and action-reaction) is crucial for correctly applying the concepts of acceleration and force.
4. Units and Conversions: Ensure that all quantities are expressed in the appropriate units (e.g., meters, kilograms, newtons) and perform necessary unit conversions if required.

Conclusion

Mastering the techniques for finding acceleration and force is essential for understanding and analyzing the motion of objects in classical mechanics. By following the step-by-step process outlined in this guide, you can confidently tackle a wide range of problems involving the calculation of acceleration and force. Remember to practice regularly and apply the concepts to real-world scenarios to solidify your understanding.

Reference:

1. https://study.com/skill/learn/how-to-calculate-the-acceleration-of-an-object-on-an-inclined-plane-explanation.html
2. https://flexbooks.ck12.org/cbook/ck-12-middle-school-physical-science-flexbook-2.0/section/11.4/primary/lesson/calculating-acceleration-from-force-and-mass-ms-ps/
3. https://www.physicsclassroom.com/class/newtlaws/Lesson-3/Finding-Acceleration