Rubber bands are a common household item that can be used to store and release elastic energy. Estimating the elastic energy storage in rubber bands is crucial for various applications, such as in the design of catapults, slingshots, and other energy-storing devices. In this comprehensive guide, we will delve into the details of how to estimate the elastic energy storage in rubber bands, covering key factors, formulas, and practical examples.
Understanding Rubber Band Elasticity
Rubber bands exhibit elastic behavior, which means they can store energy when stretched and release that energy when they return to their original shape. The ability of a rubber band to store energy is determined by its spring constant, which is a measure of the band’s stiffness.
Hooke’s Law and Spring Constant
The relationship between the force applied to a rubber band and the resulting displacement is described by Hooke’s Law. Hooke’s Law states that the force required to stretch a rubber band is proportional to the distance it is stretched, and the constant of proportionality is the spring constant, denoted as k.
The mathematical expression of Hooke’s Law is:
F = -kx
where:
– F is the force applied to the rubber band (in Newtons)
– x is the displacement or stretch distance of the rubber band (in meters)
– k is the spring constant of the rubber band (in Newtons per meter, N/m)
The negative sign in the equation indicates that the force is a restoring force, meaning it acts to return the rubber band to its original length.
Determining the Spring Constant
To determine the spring constant of a rubber band, you can perform a simple experiment. Attach one end of the rubber band to a fixed support and the other end to a force sensor or a scale. Gradually stretch the rubber band and record the force required to achieve different stretch distances. The slope of the force-displacement graph will give you the spring constant k.
Calculating Elastic Potential Energy
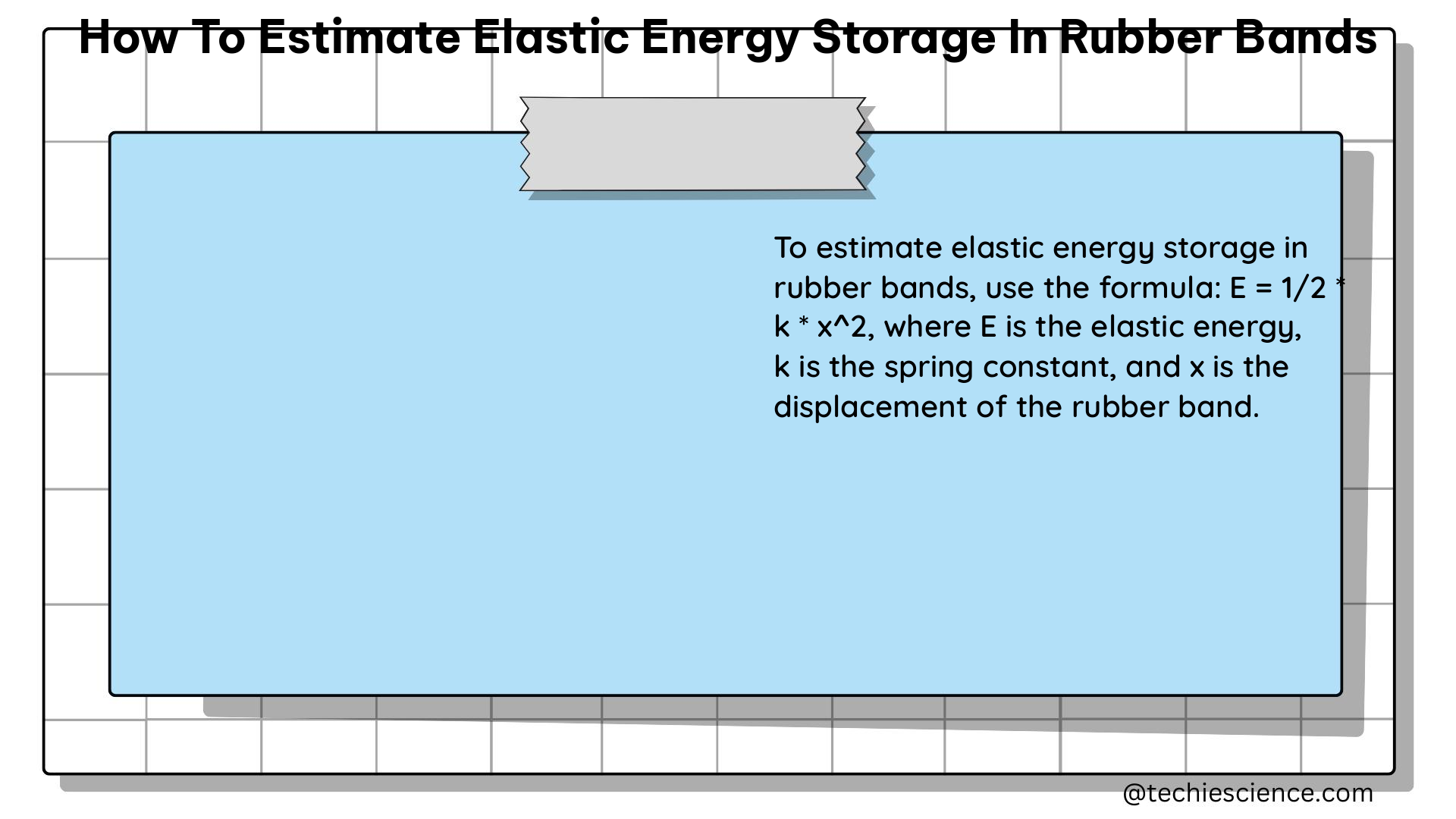
The energy stored in a stretched rubber band is known as elastic potential energy. This energy can be calculated using the formula:
U = 0.5 * k * x^2
where:
– U is the elastic potential energy stored in the rubber band (in Joules)
– k is the spring constant of the rubber band (in Newtons per meter, N/m)
– x is the displacement or stretch distance of the rubber band (in meters)
This formula shows that the energy stored in the rubber band is proportional to the square of the stretch distance.
Example Calculation
Let’s consider a rubber band with the following properties:
– Spring constant, k = 90.8 N/m
– Stretch distance, x = 0.2 m
Using the formula for elastic potential energy, we can calculate the energy stored in the rubber band:
U = 0.5 * k * x^2
U = 0.5 * 90.8 N/m * (0.2 m)^2
U = 1.8 J
This means that the rubber band can store 1.8 Joules of elastic potential energy when stretched by 0.2 meters.
Energy Density and Specific Energy
In addition to the total energy stored, it is also important to consider the energy density and specific energy of the rubber band.
Energy Density
Energy density is a measure of the energy stored per unit volume of the rubber band. It can be calculated as:
Energy Density = U / V
where:
– U is the elastic potential energy stored in the rubber band (in Joules)
– V is the volume of the rubber band (in cubic meters, m^3)
For a rectangular rubber band with length L, width W, and thickness T, the volume can be calculated as:
V = L * W * T
Specific Energy
Specific energy is a measure of the energy stored per unit mass of the rubber band. It can be calculated as:
Specific Energy = U / m
where:
– U is the elastic potential energy stored in the rubber band (in Joules)
– m is the mass of the rubber band (in kilograms, kg)
The mass of the rubber band can be calculated using its density ρ and volume V:
m = ρ * V
Example Calculations
Continuing the previous example, let’s assume the following additional properties for the rubber band:
– Length, L = 0.1 m
– Width, W = 0.005 m
– Thickness, T = 0.002 m
– Density, ρ = 1100 kg/m^3
-
Calculating the volume:
V = L * W * T = 0.1 m * 0.005 m * 0.002 m = 1 x 10^-7 m^3 -
Calculating the energy density:
Energy Density = U / V = 1.8 J / (1 x 10^-7 m^3) = 1.8 x 10^7 J/m^3 -
Calculating the mass:
m = ρ * V = 1100 kg/m^3 * (1 x 10^-7 m^3) = 1.1 x 10^-4 kg -
Calculating the specific energy:
Specific Energy = U / m = 1.8 J / (1.1 x 10^-4 kg) = 16.36 x 10^3 J/kg
These calculations show that the rubber band can store 1.8 Joules of elastic potential energy, with an energy density of 1.8 x 10^7 J/m^3 and a specific energy of 16.36 x 10^3 J/kg.
Twisting Rubber Bands
In addition to stretching, rubber bands can also store energy by twisting them around an axis. The energy stored in a twisted rubber band can be calculated using the formula for rotational energy:
U = 0.5 * k_r * θ^2
where:
– U is the rotational energy stored in the twisted rubber band (in Joules)
– k_r is the rotational spring constant of the rubber band (in Newton-meters per radian, N·m/rad)
– θ is the twisting angle of the rubber band (in radians)
The relationship between the torque τ and the twisting angle θ is given by:
τ = -k_r * θ
where:
– τ is the torque applied to the rubber band (in Newton-meters, N·m)
– k_r is the rotational spring constant of the rubber band (in Newton-meters per radian, N·m/rad)
– θ is the twisting angle of the rubber band (in radians)
By understanding the rotational energy storage in twisted rubber bands, you can explore additional applications and design considerations for energy-storing devices.
Conclusion
In this comprehensive guide, we have explored the key concepts and formulas necessary to estimate the elastic energy storage in rubber bands. By understanding the spring constant, Hooke’s Law, and the formulas for elastic potential energy, energy density, and specific energy, you can accurately calculate the energy-storing capabilities of rubber bands. Additionally, we have discussed the energy storage in twisted rubber bands, providing a more complete understanding of the various ways rubber bands can be used to store and release energy.
With this knowledge, you can apply these principles to design and optimize energy-storing devices, such as catapults, slingshots, and other applications that rely on the elastic properties of rubber bands. Remember to always consider the specific properties of the rubber bands you are working with and perform necessary experiments to determine their spring constants and other relevant parameters.
References
- How Much Energy Can You Store in a Rubber Band? – WIRED
- Calculating Energy Stored in a Twisted Rubber Band – Physics Forums
- Lab: Rubber Band Energy – SciGen Teacher Dashboard
- Rubber Bands for Energy | Science Project – Science Buddies
- Bring Science Home: Rubber Bands and Energy – Scientific American

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.