Mastering the Art of Determining Velocity in Pendulum Motion

Determining the velocity in pendulum motion is a fundamental concept in classical mechanics, and understanding this process is crucial for students and researchers alike. This comprehensive guide will delve into the intricacies of using the law of conservation of energy to calculate the velocity of a pendulum at any point during its swing.

Understanding the Fundamentals of Pendulum Motion

A pendulum is a mass suspended from a fixed point by a string or rod, which oscillates back and forth due to the force of gravity. The motion of a pendulum is described as simple harmonic motion, where the acceleration of the pendulum is proportional to the displacement from its equilibrium position.

The key factors that influence the velocity of a pendulum are:

1. Mass of the Pendulum (m): The mass of the pendulum bob or weight.
2. Length of the Pendulum (l): The length of the string or rod supporting the pendulum.
3. Acceleration due to Gravity (g): The acceleration experienced by the pendulum due to the Earth’s gravitational pull.
4. Angle of Displacement (θ): The angle between the pendulum’s position and its equilibrium position.

Applying the Law of Conservation of Energy

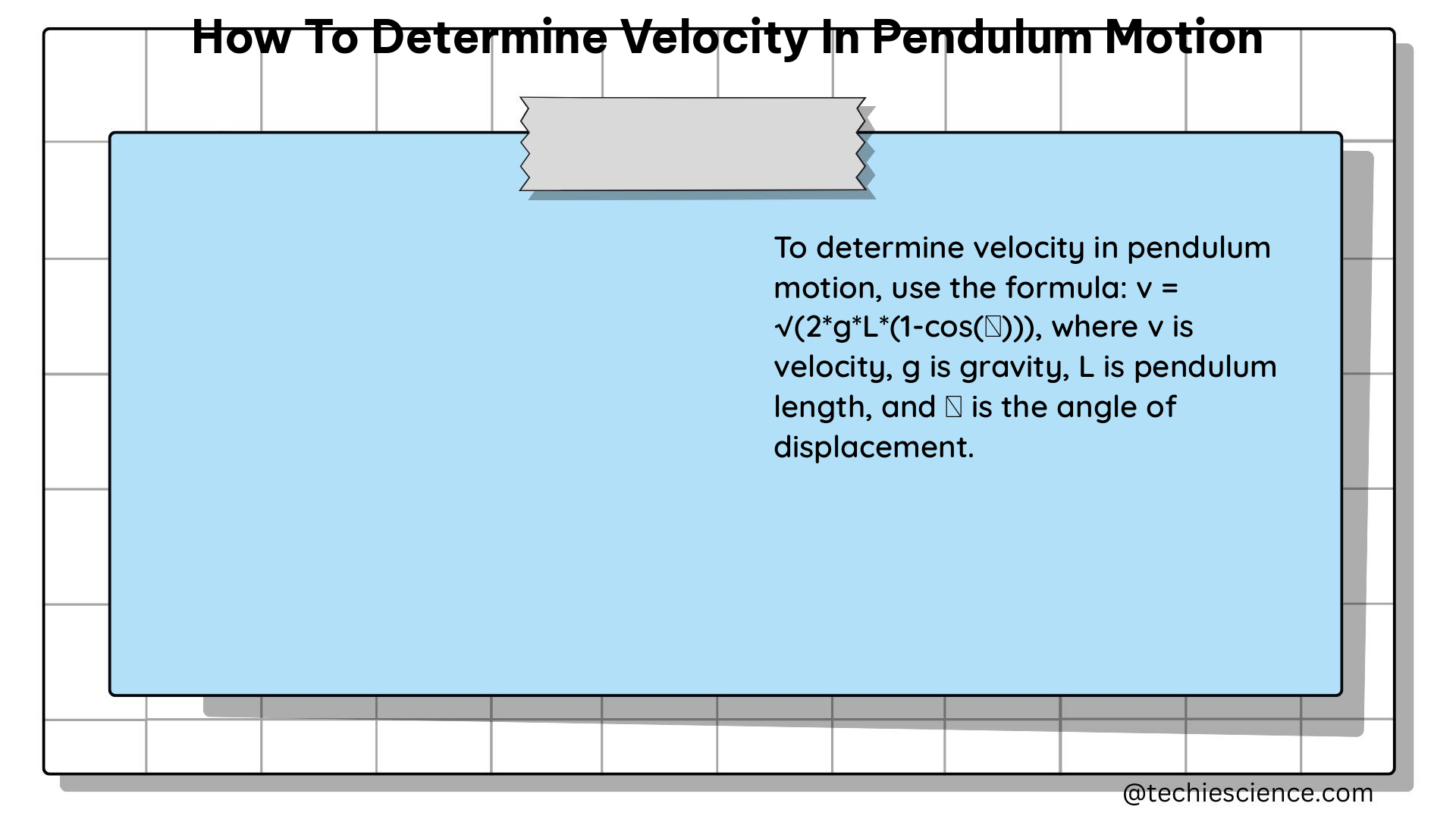
The law of conservation of energy states that the total mechanical energy of a system remains constant, and it is the sum of the potential energy and the kinetic energy. This principle can be applied to determine the velocity of a pendulum at any point in its swing.

The potential energy (PE) of the pendulum is given by the formula:

PE = mgh

where m is the mass of the pendulum, g is the acceleration due to gravity, and h is the height of the pendulum above its equilibrium position.

The kinetic energy (KE) of the pendulum is given by the formula:

KE = 1/2 mv^2

where m is the mass of the pendulum and v is the velocity of the pendulum.

At the highest point in the swing, the pendulum has maximum potential energy and zero kinetic energy. At the lowest point in the swing, the pendulum has maximum kinetic energy and zero potential energy.

To find the velocity of the pendulum at any point in its swing, we can use the law of conservation of energy to solve for v:

mgh + 1/2 mv^2 = constant

At the equilibrium position, the height (h) of the pendulum is zero, so the potential energy is also zero. Therefore, the total mechanical energy is equal to the kinetic energy at the equilibrium position.

We can solve for the velocity (v) of the pendulum at the equilibrium position using the formula:

1/2 mv^2 = mgh
v = sqrt(2gh)

where g is the acceleration due to gravity and h is the height of the pendulum above its equilibrium position.

Example Calculation

Let’s consider an example to illustrate the process of determining the velocity of a pendulum.

Suppose the length of the pendulum is 0.85 meters, the mass of the pendulum is 0.35 kilograms, and the angle of displacement is 35 degrees.

First, we need to find the height (h) of the pendulum above its equilibrium position. We can use the formula:

h = l - l cos(θ)

where l is the length of the pendulum and θ is the angle of displacement.

Plugging in the values, we get:

h = 0.85 m - 0.85 m cos(35 degrees)
h = 0.14 meters

Now, we can find the maximum velocity of the pendulum using the formula:

v = sqrt(2gh)
v = sqrt(2 * 9.81 m/s^2 * 0.14 m)
v = 0.52 m/s

Therefore, the maximum velocity of the pendulum as it swings through its equilibrium position is 0.52 m/s.

Factors Affecting Pendulum Velocity

Several factors can influence the velocity of a pendulum, and understanding these factors is crucial for accurate calculations:

1. Length of the Pendulum: The length of the pendulum directly affects the velocity. Longer pendulums have a lower velocity, while shorter pendulums have a higher velocity.
2. Mass of the Pendulum: The mass of the pendulum does not affect the velocity, as it cancels out in the velocity equation. However, the mass does affect the kinetic and potential energies of the pendulum.
3. Angle of Displacement: The angle of displacement determines the height of the pendulum above its equilibrium position, which in turn affects the velocity.
4. Acceleration due to Gravity: The acceleration due to gravity (g) is a constant that influences the velocity of the pendulum. A higher value of g will result in a higher velocity.

Advanced Considerations

For more complex pendulum systems, there are additional factors to consider:

1. Damping: Real-world pendulums experience damping due to air resistance and other dissipative forces, which can affect the velocity and the overall motion of the pendulum.
2. Nonlinear Effects: When the angle of displacement becomes large, the motion of the pendulum becomes nonlinear, and the simple harmonic motion approximation may no longer be valid.
3. Coupled Oscillations: In some cases, the pendulum may be coupled with other oscillating systems, leading to more complex motion and velocity patterns.

Practical Applications and Further Exploration

The understanding of pendulum motion and the ability to determine its velocity have numerous practical applications, including:

• Timekeeping: Pendulum clocks rely on the consistent period of pendulum oscillations to keep accurate time.
• Seismology: Pendulums are used in seismometers to detect and measure the motion of the Earth during earthquakes.
• Mechanical Vibrations: Pendulum-based systems are used to study and control mechanical vibrations in various engineering applications.
• Pendulum Waves: The interaction of multiple pendulums can create fascinating wave patterns, which have applications in art, music, and education.

To further explore the topic of pendulum motion and velocity, you can delve into the following resources:

Reference:
1. Pendulum Velocity – YouTube, https://www.youtube.com/watch?v=VLM_6i2ce0k
2. How to Calculate the Velocity of a Pendulum Using the Law of Conservation of Energy – Explanation, https://study.com/skill/learn/how-to-calculate-the-velocity-of-a-pendulum-using-the-law-of-conservation-of-energy-explanation.html
3. Simple Harmonic Motion (6 of 16): Pendulum Velocity from Angle of Displacement – Video, https://www.youtube.com/watch?v=iuTxZHpxj7E