Stellar dynamics is a field of astrophysics that focuses on the motion and interaction of stars within a galaxy or other stellar system. Accurately computing the velocity of stars is crucial for understanding the structure, evolution, and dynamics of these systems. In this comprehensive guide, we will delve into the various techniques and formulas used to compute velocity in stellar dynamics, providing you with a detailed and technical manual to enhance your understanding and application of these concepts.
Radial Velocity Measurement Using the Doppler Shift
The primary method for computing the radial velocity of a star is through the analysis of its spectral lines. When a star is moving relative to an observer, the wavelengths of the absorption lines in the star’s spectrum are shifted due to the Doppler effect. This shift can be used to calculate the radial velocity of the star using the following formula:
v = c * (λobs - λlab) / λlab
Where:
– v is the radial velocity of the star
– c is the speed of light (3.0 × 10^8 m/s)
– λobs is the observed wavelength of the spectral line
– λlab is the laboratory-measured wavelength of the same spectral line
For example, if the observed wavelength of the Hα (first Balmer line of hydrogen) in a star’s spectrum is 657.0 nm, and the laboratory-measured wavelength of Hα is 656.28 nm, the radial velocity of the star can be calculated as:
v = (3.0 × 10^8 m/s) * (657.0 nm - 656.28 nm) / 656.28 nm = 300 km/s
This indicates that the star is moving away from the observer at a speed of 300 km/s.
Proper Motion Measurement
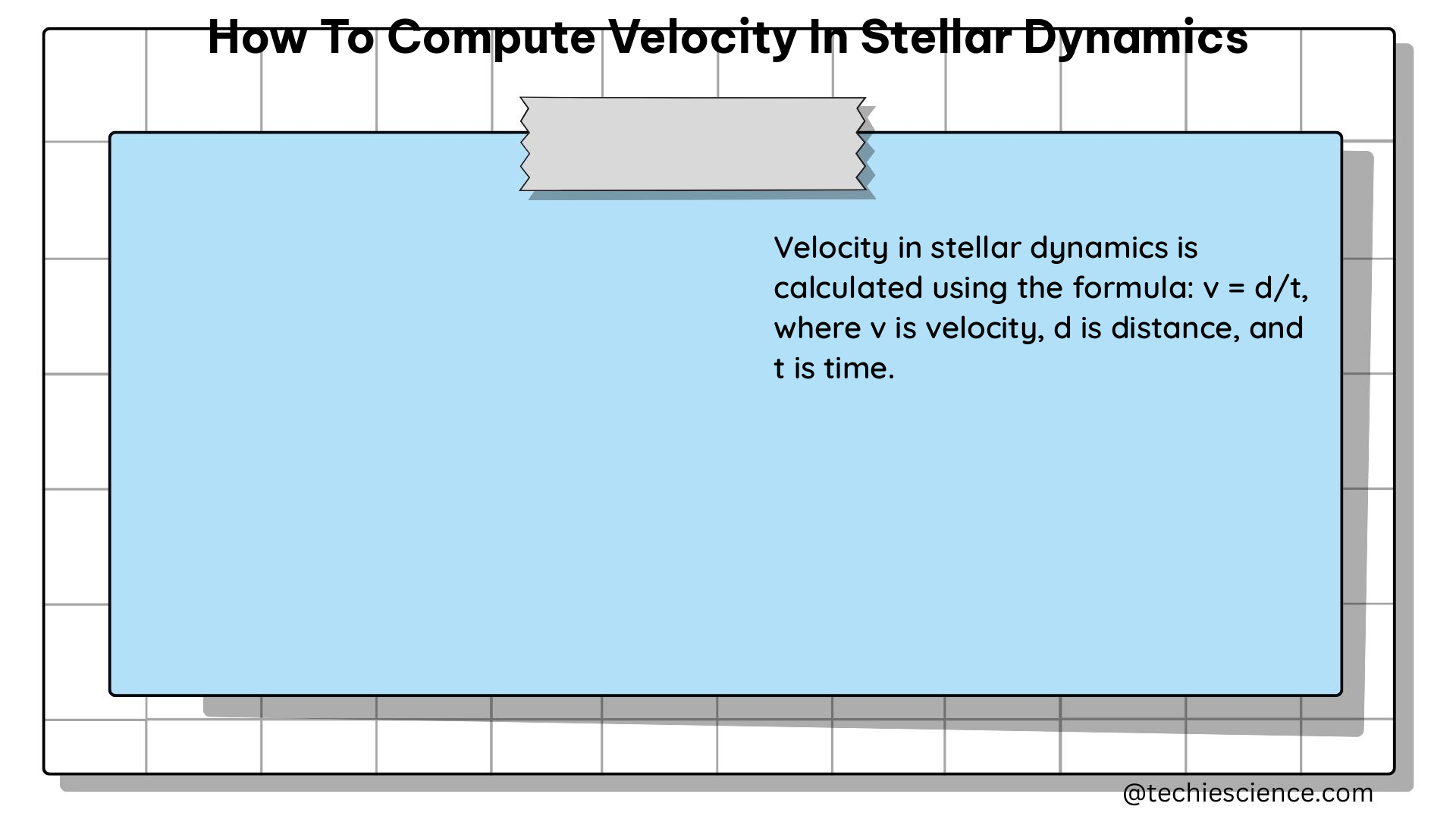
In addition to radial velocity, the proper motion of a star can also be used to compute its velocity. Proper motion is the apparent motion of a star across the sky, perpendicular to the line of sight. It is typically measured in arcseconds per year and can be calculated by comparing the position of a star in different epochs of observations.
The proper motion components in right ascension (μα) and declination (μδ) can be calculated as:
μα = (α2 - α1) / Δt
μδ = (δ2 - δ1) / Δt
Where:
– α1, δ1 are the right ascension and declination of the star in the first epoch
– α2, δ2 are the right ascension and declination of the star in the second epoch
– Δt is the time difference between the two observations
By combining the radial velocity and proper motion measurements, you can obtain the full three-dimensional velocity vector of a star, which is essential for understanding its dynamics within a stellar system.
Stellar Velocity Distributions
Stellar velocities within a galaxy or stellar system often exhibit characteristic distributions that provide insights into the system’s structure and evolution. Some common velocity distributions include:
-
Gaussian Distribution: Many stellar systems, such as the Milky Way’s disk, exhibit a Gaussian (normal) distribution of velocities, reflecting the random motions of stars within the system.
-
Anisotropic Velocity Distributions: Some stellar systems, such as the Milky Way’s bulge or globular clusters, can have anisotropic velocity distributions, where the velocities in different directions (e.g., radial, tangential) have different dispersions.
-
Multimodal Distributions: Stellar systems with multiple kinematic components, such as the Milky Way’s disk and halo, can exhibit multimodal velocity distributions, with distinct peaks corresponding to the different components.
Understanding these velocity distributions and their underlying causes is crucial for studying the dynamics and evolution of stellar systems.
Numerical Simulations of Stellar Dynamics
Computational simulations play a vital role in the study of stellar dynamics, allowing researchers to model the complex interactions and evolution of stars within a stellar system. These simulations often involve solving the equations of motion for individual stars or using statistical approaches to model the collective behavior of a large number of stars.
One widely used technique is N-body simulations, where the gravitational interactions between individual stars are explicitly calculated. These simulations can provide detailed insights into the formation, evolution, and stability of stellar systems, as well as the role of various physical processes, such as stellar encounters, tidal interactions, and the presence of dark matter.
Another approach is to use collisionless Boltzmann equations, which describe the evolution of the phase-space distribution function of stars in a stellar system. This statistical approach can be used to study the large-scale properties of stellar systems, such as the velocity distribution and the overall structure of the system.
Observational Challenges and Techniques
Measuring the velocities of stars in stellar systems can be challenging due to various observational limitations and uncertainties. Some key considerations include:
-
Spectral Resolution: The ability to accurately measure the wavelength shifts of spectral lines is limited by the spectral resolution of the observational instruments.
-
Stellar Variability: Intrinsic variations in a star’s brightness and spectral properties can introduce uncertainties in the velocity measurements.
-
Crowded Fields: In dense stellar environments, such as the Galactic center, the blending of spectral lines from nearby stars can complicate the velocity measurements.
-
Astrometric Precision: Precise measurements of a star’s position over time are required to accurately determine its proper motion.
To overcome these challenges, astronomers employ a variety of observational techniques and data analysis methods, such as high-resolution spectroscopy, adaptive optics, and advanced statistical techniques for separating the various contributions to the observed velocities.
Applications and Implications
The accurate computation of stellar velocities has numerous applications and implications in the field of stellar dynamics and astrophysics, including:
-
Galactic Structure and Evolution: Studying the velocity distributions of stars within a galaxy can provide insights into the galaxy’s structure, such as the presence of distinct kinematic components (e.g., disk, bulge, halo), and its evolutionary history.
-
Dynamical Modeling: Velocity measurements are essential for constructing dynamical models of stellar systems, which can be used to infer the presence and properties of dark matter, supermassive black holes, and other gravitational influences.
-
Exoplanet Detection: The radial velocity method, which relies on the Doppler shift of spectral lines, is a widely used technique for detecting exoplanets orbiting distant stars.
-
Stellar Streams and Tidal Interactions: Analyzing the velocities of stars in tidal streams and disrupted stellar systems can reveal information about the gravitational forces and interactions that shaped these structures.
-
Stellar Kinematics and Dynamics: Detailed studies of the velocity distributions and motions of stars within a stellar system can provide insights into the underlying physical processes, such as stellar encounters, binary formation, and the role of different gravitational fields.
By mastering the techniques for computing stellar velocities, you can contribute to our understanding of the complex and fascinating world of stellar dynamics, with implications that span from the structure of our own Milky Way galaxy to the detection of exoplanets and the evolution of the Universe as a whole.
References:
- Simola, U., Bonfanti, A., Dumusque, X., Cisewski-Kehe, J., Kaski, S., & Corander, J. (2022). Accounting for stellar activity signals in radial-velocity data by using change point detection techniques. Astronomy & Astrophysics, 664, A127.
- Merritt, D. (1999). Stellar dynamics around black holes. IOPscience.
- Dutton, K. (n.d.). Stellar Velocities | Astronomy 801 – Dutton Institute – Penn State. Retrieved from https://www.e-education.psu.edu/astro801/content/l4_p7.html
- Binney, J., & Tremaine, S. (2008). Galactic dynamics. Princeton university press.
- Kuijken, K., & Dubath, P. (1998). Stellar dynamics in the Galactic Centre: proper motions and anisotropy. Monthly Notices of the Royal Astronomical Society, 317(2), 348-360.

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.