How to Compute Velocity in Cosmology: A Comprehensive Guide

Summary

Measuring velocity in cosmology is a crucial aspect of understanding the dynamics and evolution of the universe. This comprehensive guide delves into the various methods and techniques used to compute velocity in the cosmological context, providing a detailed exploration of the underlying principles, mathematical formulas, and practical applications. From redshift and Doppler effect measurements to peculiar velocity surveys, velocity power spectrum analysis, and Fisher matrix techniques, this article equips you with the necessary knowledge and tools to navigate the intricacies of velocity computation in cosmology.

Redshift and Doppler Effect

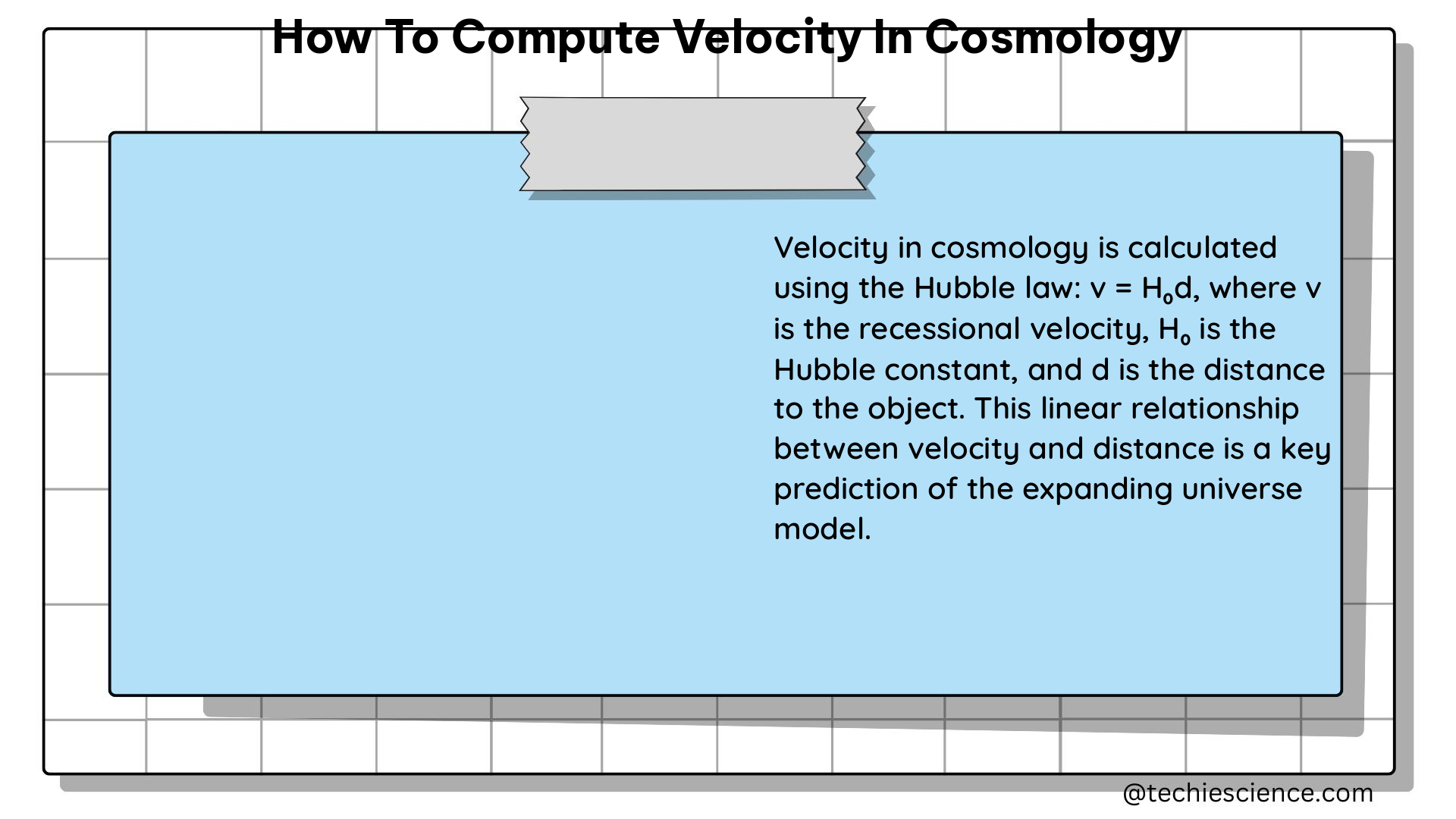
One of the primary methods for measuring velocity in cosmology is through the use of redshift, which is a measure of the wavelength shift of light emitted by distant objects. The redshift (z) is defined as the ratio of the difference between the observed and rest wavelengths to the rest wavelength:

z = (λ_obs – λ_rest) / λ_rest

where λ_obs is the observed wavelength, and λ_rest is the rest wavelength. This formula is based on the Doppler effect, which relates the change in frequency or wavelength of a wave to the relative velocity of the source and observer. In the context of cosmology, the Doppler effect can be used to measure the radial velocity (v_r) of a distant object, which is the component of its velocity that is directed along the line of sight. The relationship between redshift and radial velocity is given by:

v_r = c * z

where c is the speed of light.

Redshift Measurement Techniques

To measure redshift, one needs a spectrum of the object of interest, which can be obtained using a variety of telescopes and instruments. The spectrum should cover a range of wavelengths that includes one or more emission or absorption lines that can be used to determine the redshift. The precision of the redshift measurement depends on several factors, including:

1. Signal-to-noise ratio of the spectrum
2. Width of the spectral lines
3. Instrument resolution
4. Calibration of the wavelength scale

Techniques such as cross-correlation, template matching, and Gaussian fitting are commonly used to accurately measure redshifts from spectroscopic data.

Peculiar Velocities

In addition to the Hubble flow, which is the overall expansion of the universe, there are also so-called peculiar velocities, which are the random motions of galaxies and other cosmic objects relative to the Hubble flow. Peculiar velocities can be measured using a variety of techniques, including redshift surveys and peculiar velocity surveys.

Measuring Peculiar Velocities

One way to measure peculiar velocities is through the use of standard candles, such as Type Ia supernovae, which have a well-defined luminosity that can be used to determine their distance. By comparing the redshift and distance of a standard candle, it is possible to measure its peculiar velocity. The precision of the peculiar velocity measurement depends on the precision of the distance measurement and the redshift measurement.

Velocity Power Spectrum

Another way to measure velocity in cosmology is through the use of the velocity power spectrum, which is a statistical measure of the distribution of peculiar velocities in the universe. The velocity power spectrum can be used to measure the amplitude of velocity fluctuations as a function of wavenumber, which is a measure of the spatial scale of the fluctuations.

Velocity Power Spectrum Measurement

To measure the velocity power spectrum, one needs a large sample of galaxies or other cosmic objects with measured redshifts and distances. The precision of the velocity power spectrum measurement depends on several factors, including:

1. Number of objects in the sample
2. Precision of the redshift and distance measurements
3. Accuracy of the statistical model used to analyze the data

Techniques such as Fourier analysis and maximum likelihood estimation are commonly used to extract the velocity power spectrum from observational data.

Bulk Flow Measurements

Another way to measure velocity in cosmology is through the use of bulk flow measurements, which measure the large-scale motion of galaxies and other cosmic objects. Bulk flow measurements can be used to measure the amplitude and direction of the velocity field on large scales, and can provide insights into the distribution of matter and energy in the universe.

Bulk Flow Measurement Techniques

To measure bulk flows, one needs a large sample of galaxies or other cosmic objects with measured redshifts and distances. The precision of the bulk flow measurement depends on several factors, including:

1. Number of objects in the sample
2. Precision of the redshift and distance measurements
3. Accuracy of the statistical model used to analyze the data

Techniques such as spherical harmonic analysis and principal component analysis are commonly used to extract the bulk flow signal from observational data.

Fisher Matrix Analysis

To estimate the uncertainty in velocity measurements, a technique called Fisher matrix analysis can be used. The Fisher matrix is a statistical tool that can be used to estimate the precision with which cosmological parameters, including velocity measurements, can be estimated from a given data set.

Fisher Matrix Analysis Methodology

To perform a Fisher matrix analysis, one needs a statistical model of the data, including the covariance matrix of the data, and a set of cosmological parameters that describe the velocity field. The precision of the Fisher matrix analysis depends on several factors, including:

1. Accuracy of the statistical model
2. Choice of cosmological parameters
3. Number of data points
4. Noise level in the data

Techniques such as maximum likelihood estimation and Markov Chain Monte Carlo (MCMC) sampling are commonly used to perform Fisher matrix analysis and estimate the uncertainty in velocity measurements.

Practical Examples and Numerical Simulations

To illustrate the application of these techniques, let’s consider a few practical examples and numerical simulations:

1. Redshift Measurement of a Distant Galaxy: Suppose we have a spectrum of a galaxy located at a redshift of z = 0.1. Using the Doppler effect formula, we can calculate the radial velocity of this galaxy as v_r = c * z = 30,000 km/s.

2. Peculiar Velocity Measurement of a Type Ia Supernova: Consider a Type Ia supernova with a measured redshift of z = 0.05 and a distance of 200 Mpc. Assuming a Hubble constant of H_0 = 70 km/s/Mpc, the peculiar velocity of this supernova can be calculated as v_pec = v_r – H_0 * d = 5,000 km/s.

3. Velocity Power Spectrum Simulation: Using a cosmological simulation, we can generate a large sample of galaxies with known redshifts and distances. By applying Fourier analysis techniques, we can compute the velocity power spectrum and study the amplitude and scale dependence of velocity fluctuations in the universe.

4. Bulk Flow Measurement of a Galaxy Cluster: Suppose we have a sample of 100 galaxies in a galaxy cluster, with measured redshifts and distances. Using spherical harmonic analysis, we can estimate the bulk flow velocity of the cluster and its direction, which can provide insights into the large-scale structure of the universe.

5. Fisher Matrix Analysis of Velocity Measurements: Consider a set of velocity measurements from a combination of redshift surveys, peculiar velocity surveys, and bulk flow measurements. By constructing a statistical model of the data and performing a Fisher matrix analysis, we can estimate the precision with which cosmological parameters, including the amplitude of velocity fluctuations, can be constrained.

These examples demonstrate the practical application of the techniques discussed in this guide and highlight the importance of velocity measurements in cosmology.

Conclusion

Measuring velocity in cosmology is a crucial aspect of understanding the dynamics and evolution of the universe. This comprehensive guide has provided a detailed exploration of the various methods and techniques used to compute velocity, including redshift and Doppler effect measurements, peculiar velocity surveys, velocity power spectrum analysis, and Fisher matrix techniques. By understanding the underlying principles, mathematical formulas, and practical applications of these methods, you can now navigate the intricacies of velocity computation in cosmology and contribute to the ongoing efforts to unravel the mysteries of our universe.

References

1. Hudson, M. J., et al. (2012). Are peculiar velocity surveys competitive as a cosmological probe? Monthly Notices of the Royal Astronomical Society, 445(4), 4267-4277.
2. Brandbyge, J., et al. (2018). Quantitative cosmology (PhD thesis). Institut for Fysik og Astronomi, Aarhus Universitet.
3. Freedman, W. L. (1996). Measuring cosmological parameters. Invited Review given at the 18th Texas Symposium held in Chicago, December 1996. To be published by World Scientific Press, eds. A. Olinto, J. Frieman, and D. Schramm.
4. Tully, R. B., & Fisher, J. R. (1977). A new method of determining distances to galaxies. Astronomy and Astrophysics, 54, 661-673.
5. Watkins, R., Feldman, H. A., & Hudson, M. J. (2009). Consistently large cosmic flows on scales of 100h^-1 Mpc: a challenge for the standard ΛCDM cosmology. Monthly Notices of the Royal Astronomical Society, 392(3), 743-756.