How to Calculate the Velocity of a String

Summary

The velocity of a wave traveling along a string can be calculated using the formula v = √(F/μ), where v is the velocity of the wave, F is the tension in the string, and μ is the linear density of the string. This formula is derived from the wave equation and is equivalent to the kinematic formula v = Δd/Δt, where Δd is the change in distance and Δt is the change in time. The angular frequency of the wave also plays a role in determining the maximum velocity of the wave’s particles. Additionally, the time-averaged power supplied to the wave by the string vibrator can be calculated using the formula P = 1/2 * μ * A^2 * ω^2 * v, where P is the time-averaged power, A is the amplitude of the wave, and ω is the angular frequency of the wave.

Understanding the Wave Velocity Formula

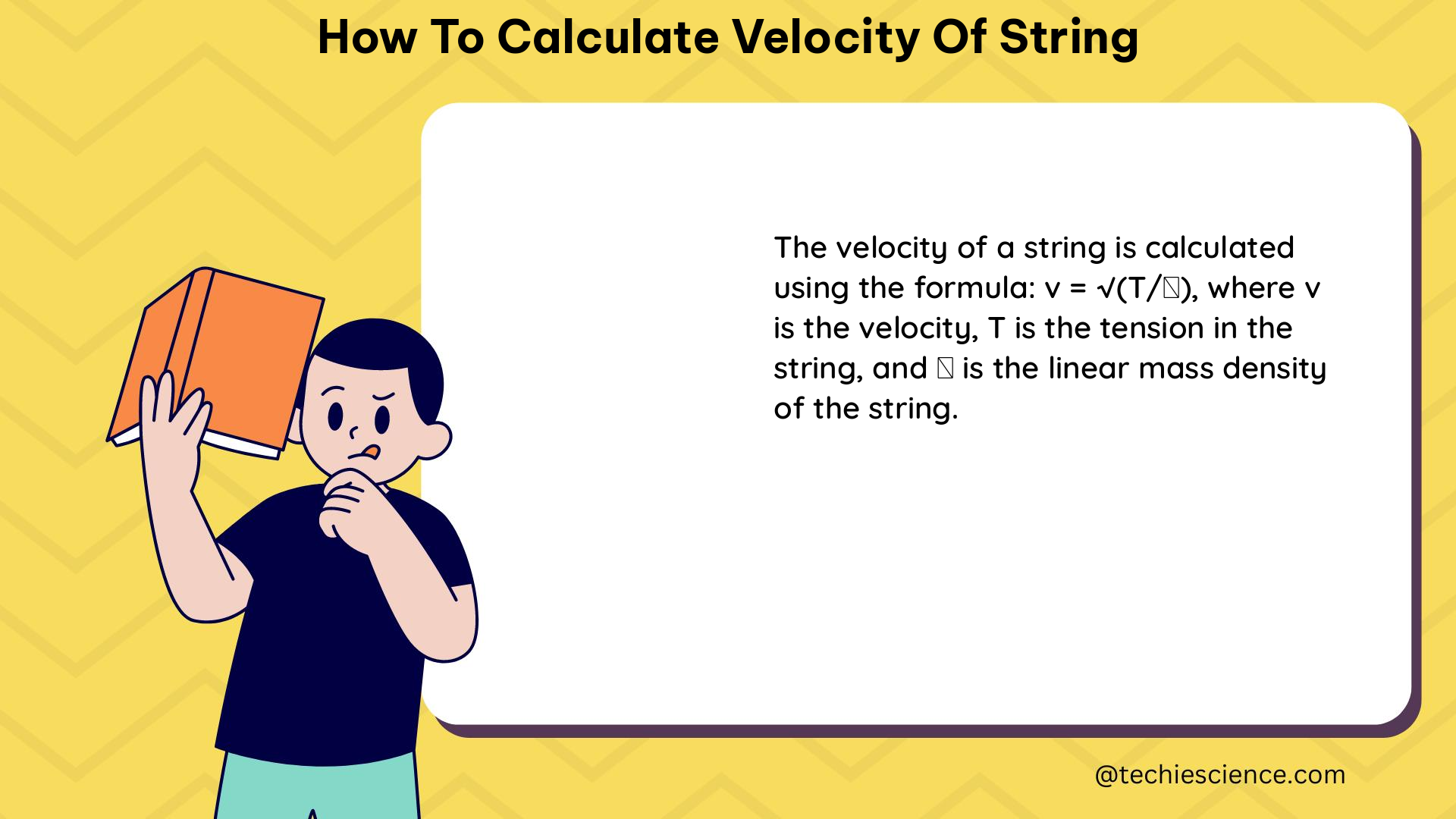
The formula for the velocity of a wave traveling along a string is:

v = √(F/μ)

where:

• v is the velocity of the wave in the string
• F is the tension in the string
• μ is the linear density of the string

The linear density μ is calculated by dividing the mass of the string by its length:

μ = m/L

where:

• m is the mass of the string
• L is the length of the string

This formula is derived from the wave equation, which describes the propagation of waves along a string. The wave equation is:

∂^2 y/∂t^2 = (F/μ) * ∂^2 y/∂x^2

where y is the displacement of the string from its equilibrium position, t is time, and x is the position along the string.

By solving the wave equation, we can arrive at the formula v = √(F/μ) for the velocity of the wave.

Kinematic Formula for Wave Velocity

The velocity of a wave can also be calculated using the kinematic formula:

v = Δd/Δt

where:

• v is the velocity of the wave
• Δd is the change in distance
• Δt is the change in time

This formula is derived from the definition of velocity as the ratio of displacement to time. In the context of a string wave, the kinematic formula can be used to measure the velocity of the wave by observing the time it takes for a disturbance to travel a certain distance along the string.

Angular Frequency and Wave Velocity

In the context of a string wave, the angular frequency ω helps us determine how fast the string’s particles vibrate as the wave travels along the string. The angular frequency is related to the frequency f of the wave by the formula:

ω = 2πf

Higher angular frequency indicates quicker oscillations, which, in turn, affects the maximum velocity of the wave’s particles. The relationship between angular frequency and wave velocity is important in understanding the energy and power of the wave, as discussed in the next section.

Energy and Power of a String Wave

The time-averaged power supplied to the wave by the string vibrator is given by the formula:

P = 1/2 * μ * A^2 * ω^2 * v

where:

• P is the time-averaged power
• μ is the linear density of the string
• A is the amplitude of the wave
• ω is the angular frequency of the wave
• v is the velocity of the wave

This formula shows that the power supplied to the wave is proportional to the square of the amplitude of the wave and the square of the angular frequency of the wave. The velocity of the wave also plays a role in the power supplied to the wave.

Experimental Verification of Wave Velocity Formulas

Experiment 1: Relationship between Wave Velocity and String Tension

In an experiment, the relationship between wave velocity and string tension was studied by examining standing waves of a string. The data gathered was used to find the wavelengths of strings at different tensions and calculate the mass per unit of length (linear density) of each string tension.

The results showed that the slope for investigation two was within the calculated uncertainty of the actual value, thereby proving the equation v = f * λ, where v is the velocity, f is the frequency, and λ is the wavelength. This equation is derived from the wave velocity formula v = √(F/μ) and the relationship between frequency, wavelength, and wave velocity.

Experiment 2: Measuring the Speed of Sound

In another experiment, the speed of sound was measured by studying standing waves in an air column. The relationship between velocity, frequency, and wavelength was used to calculate the velocity of sound during the investigation. Wavelength was necessary in this investigation to calculate the velocity of sound, so it was calculated using the relationship between string length and wavelength.

The data collected during this experiment was the varying heights of the resonance points, which were used to find the wavelength and velocity of sound. This experiment demonstrates the practical application of the wave velocity formulas in measuring the speed of sound, which is an important physical quantity in various fields of science and engineering.

Conclusion

In summary, the velocity of a wave traveling along a string can be calculated using the formula v = √(F/μ), where F is the tension in the string and μ is the linear density of the string. This formula is derived from the wave equation and is equivalent to the kinematic formula v = Δd/Δt. The angular frequency of the wave also plays a role in determining the maximum velocity of the wave’s particles, and the time-averaged power supplied to the wave can be calculated using the formula P = 1/2 * μ * A^2 * ω^2 * v.

The formulas for wave velocity have been experimentally verified, as demonstrated by the two experiments discussed in this article. These experiments show the practical applications of the wave velocity formulas in measuring physical quantities like the speed of sound.

References

1. University Physics with Modern Physics, 2nd Edition, Chapter 15, Problem 18
2. How is the Wave Speed of a String the Same as Calculating the Speed Using Kinematics?
3. Energy and Power of a Wave
4. Coursesidekick.com – Mathematics 343762
5. University Physics (OpenStax) – Energy and Power of a Wave