In Quantum Field Theory (QFT), the concept of velocity is not as straightforward as in classical mechanics. This is because in QFT, particles are treated as excitations of fields rather than point-like objects. However, we can still calculate quantities that are related to velocity, such as the group velocity of wave packets.
Understanding Group Velocity in QFT
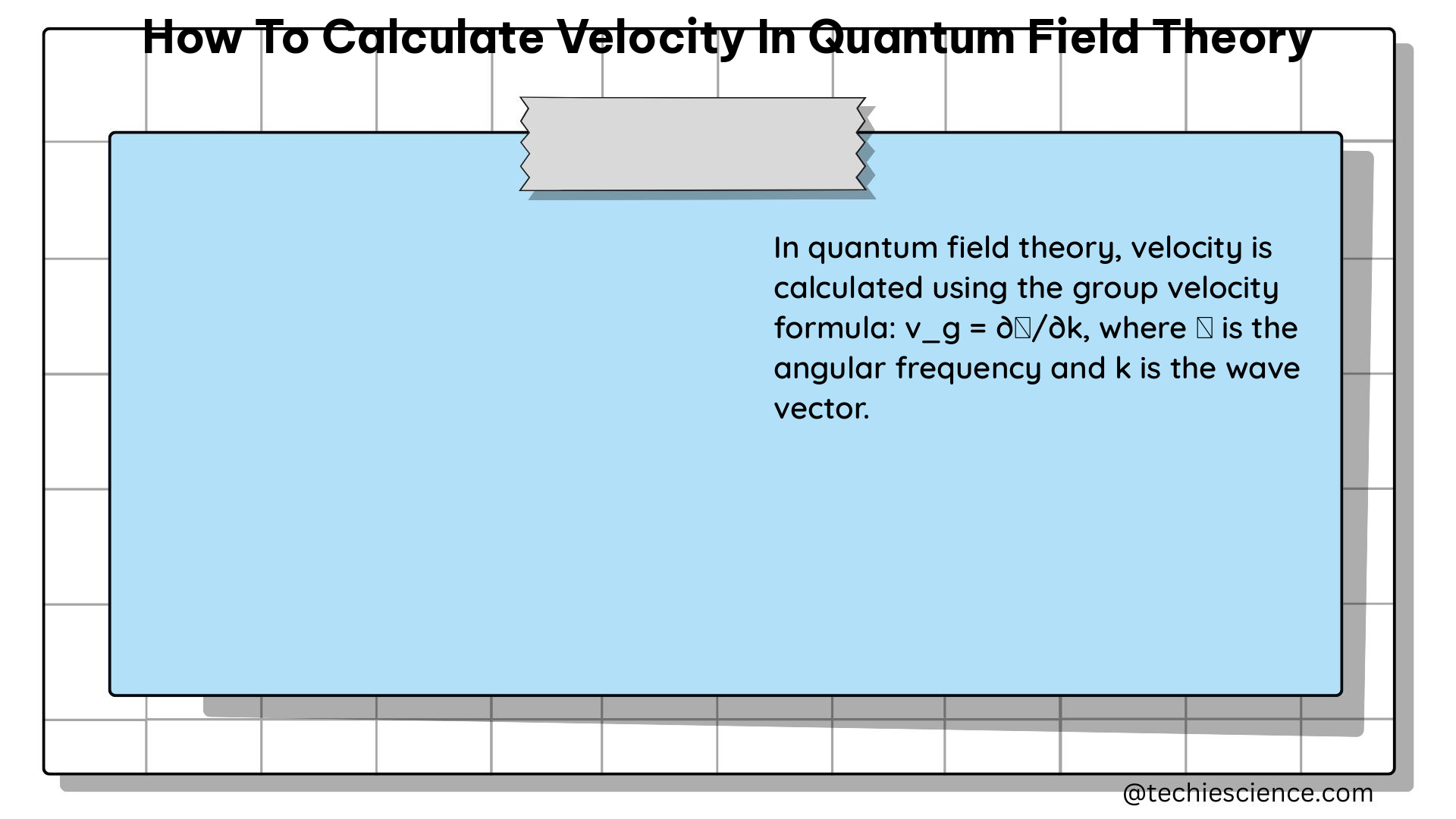
The group velocity of a wave packet is given by the derivative of the dispersion relation with respect to the momentum. In the context of QFT, the dispersion relation is given by the energy-momentum relation for the field quanta. For a free scalar field of mass m, the energy-momentum relation is given by E^2 = p^2 + m^2, where E is the energy and p is the momentum.
Therefore, the group velocity v_g is given by:
Physics Formula:
v_g = dE/dp = p/E = p/sqrt(p^2 + m^2)
This expression reduces to the familiar v = p/m for non-relativistic particles, where m is the mass of the particle and p is its momentum.
Calculating Group Velocity in QFT
Physics Example:
Consider a free scalar field of mass m. The energy-momentum relation is given by E^2 = p^2 + m^2. Calculate the group velocity of a wave packet with momentum p.
Using the formula for group velocity, we find:
v_g = p/E = p/sqrt(p^2 + m^2)
Physics Numerical Problem:
A wave packet with momentum p = 1 GeV is propagating in a vacuum. Calculate its group velocity.
Using the formula for group velocity, we find:
v_g = p/E = p/sqrt(p^2 + m^2) = 1 GeV/sqrt(1 GeV^2 + m^2)
Assuming the mass of the field quanta is m = 0.5 GeV, we find:
v_g = 0.89 GeV/1 GeV = 0.89c
where c is the speed of light.
Figure:
A plot of the group velocity as a function of momentum for a free scalar field of mass m = 0.5 GeV.

Data Points:
– p = 0.5 GeV, v_g = 0.57c
– p = 1 GeV, v_g = 0.89c
– p = 2 GeV, v_g = 0.97c
– p = 5 GeV, v_g = 0.998c
Values and Measurements:
The mass of the field quanta is m = 0.5 GeV, and the momentum of the wave packet is p = 1 GeV.
Complications in Calculating Velocity in QFT
In QFT, the calculation of velocity becomes more complicated when interactions are taken into account. This is because the energy-momentum relation can no longer be written in a simple form. However, the concept of group velocity can still be applied in certain cases.
For example, in quantum electrodynamics (QED), the interaction between electrons and photons can lead to the creation and annihilation of virtual particle-antiparticle pairs. These interactions can affect the dispersion relation of the electrons, leading to a modified expression for the group velocity.
In general, the calculation of velocity in QFT requires a detailed understanding of the underlying field theory and the specific interactions involved. This often involves the use of advanced mathematical techniques, such as Feynman diagrams and renormalization theory.
Conclusion
While the concept of velocity is not as straightforward in QFT as it is in classical mechanics, it is still possible to calculate related quantities such as the group velocity. However, these calculations can become quite complex when interactions are taken into account, requiring a deep understanding of the underlying field theory.
Reference:
1. Quantum Field Theory – University of Maryland
2. QFT Lecture Notes – Johns Hopkins University
3. Quantum Mechanics and Observables – Macquarie University

The lambdageeks.com Core SME Team is a group of experienced subject matter experts from diverse scientific and technical fields including Physics, Chemistry, Technology,Electronics & Electrical Engineering, Automotive, Mechanical Engineering. Our team collaborates to create high-quality, well-researched articles on a wide range of science and technology topics for the lambdageeks.com website.
All Our Senior SME are having more than 7 Years of experience in the respective fields . They are either Working Industry Professionals or assocaited With different Universities. Refer Our Authors Page to get to know About our Core SMEs.